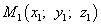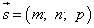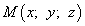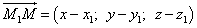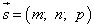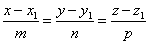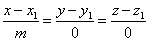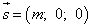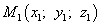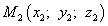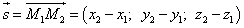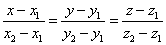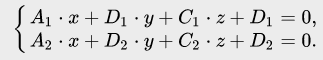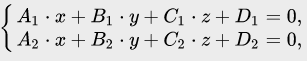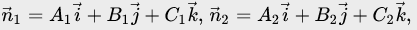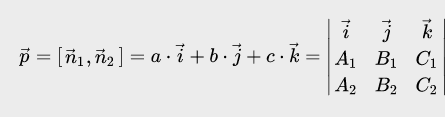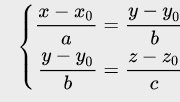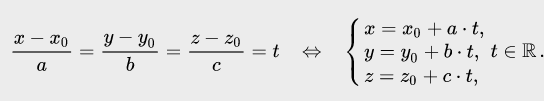Каноническое уравнение прямой в пространстве

Что такое каноническое уравнение прямой в пространстве

Допустим, что есть какая-то точка:

 

и направляющий вектор:

 

Произвольная точка:

 

принадлежит прямой l только тогда, когда векторы:

 

 

коллинеарны, то есть в данном случае можно сделать вывод о справедливости уравнения:

 

При таких условиях данные уравнения являются каноническими уравнениями прямой.

Частные случаи канонических уравнений прямой в пространстве

Числа m, n и p представляют собой проекции основного направляющего вектора на координатные оси. Исходя из того, что вектор s является ненулевым, можно сказать, что числа m, n и p в одно время не могут обладать нулевым значением. Однако допустимо, что одно или несколько из них равны нулю. В рамках аналитической геометрии справедливой может быть пример следующего выражения:

 

Данное уравнение демонстрирует нулевые значения проекций вектора s – Oy и Oz. Таким образом, вектор:

 

и прямая в виде канонических уравнений, перпендикулярны осям Oy и Oz, то есть плоскости yOz.

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

Прямую можно составить с помощью пары лежащих на ней точек:

 

 

Тогда допустима ситуация, при которой направляющий вектор прямой имеет вид:

 

Согласно вышеизложенному, канонические уравнения можно записать таким образом:

 

С помощью данных выражений можно определить прямую, которая пролегает через пару рассматриваемых точек.

Правила преобразования канонического уравнения в другие виды уравнений

Рассмотрим наиболее распространенные преобразования уравнений прямой. Запишем общее уравнение прямой:

Представим каноническое уравнение прямой:

Представить общее уравнение в виде канонического достаточно просто. Вначале необходимо определить какое-либо решение (x0; y0; z0) системы:

Таким образом, можно определить координаты точки М0, которая расположена на рассматриваемой прямой. Далее требуется найти направляющий вектор в виде векторного произведения нормалей:

на заданных плоскостях:

Далее достаточно записать каноническое уравнение, учитывая все эти действия. Таким образом, преобразуют общее уравнение в каноническое.

Обратный переход канонического уравнения в общий вид выполняют с помощью записи двойного равенства в виде системы и приведения подобных членов. Выглядеть уравнение будет таким образом:

Переход от канонического уравнения к параметрическому выполняют с помощью приравнивания каждой дроби к параметру t и записи полученного выражения в форме системы:

В том случае, когда в каноническом уравнении прямой зафиксированы координаты x0, y0, z0, принадлежащие точке М0, а коэффициенты а, b, с характеризуются произвольными значениями, то есть не равны нулю одновременно, можно записать уравнение связки прямых с центром в точке M0, то есть комплекс всех прямых, пересекающих точку М0.