Касательная к окружности
Касательная к окружности
Касательная к окружности — в геометрии это прямая, которая имеет с окружностью одну общую точку. Такая точка называется точкой касания.
У этой прямой есть ряд свойств.
Свойство №1
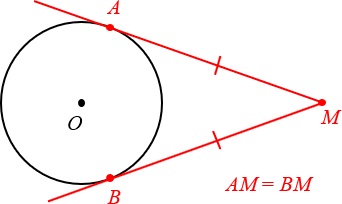
Отрезки линий касательных, проведенных из одной точки, равны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На чертеже это выглядит таким образом:
Свойство №2
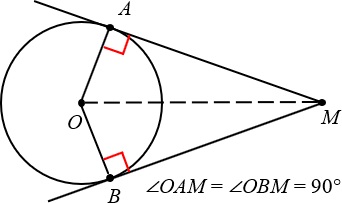
Касательная линия перпендикулярна радиусу, проведенному в точку касания.
При этом, если провести отрезок из центра окружности до начальной точки прямых (OM), мы получим два равных прямоугольных треугольника (OAM=OBM).
Свойство №3
Соотношение между касательной и секущей.
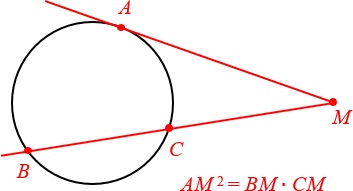
Графическое изображение этого утверждения выглядит так:
Это утверждение о касательной и секущей, которые проходят через общую точку (M). Секущая дает нам два отрезка: BC (внутренний отрезок, хорда) и CM (внешняя часть секущей). Произведение всей секущей BM на ее внешнюю часть CM равно квадрату отрезка касательной. Формула выглядит так:
\(AM^2=BM\cdot CM.\)
Свойство №4
Угол между касательной и хордой.
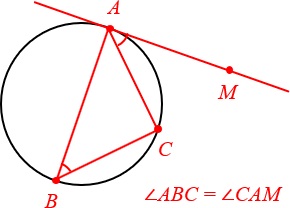
Это утверждение относится к продвинутому уровню и используется для решения сложных задач. Звучит оно так: угол между касательной и хордой равен вписанному углу, который опирается на эту хорду.
Рисунок к этому правилу:
Точка B обычно задается в условии задачи, поэтому ученику нужно лишь уметь распознавать эту конфигурацию в заданиях и уметь применять правило при решении.
Теоремы и доказательства
Отрезки касательных, проведенных из одной точки, равны и формируют равные углы с прямой, проходящей через эту точку и центр окружности.
Доказательство
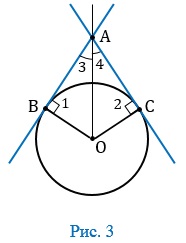
Дано: AB и AC — касательные к окружности с центром O. B и C — точки касания.
Доказать: \(AB=AC, a \angle3=\angle4.\)
Доказательство: \(\angle1=\angle2=90^\circ\), так как \(OВ\perp АВ\), \(ОС\perp АС\) согласно теореме о свойстве касательной, поэтому \(\triangle ABO\) и \(\triangle ACO\) — прямоугольные. OB и OC — радиусы, OB=OC, AO — общая сторона. Значит, \(\triangle ABO = \triangle ACO\) по гипотенузе и катету. Следовательно, уравнения AB=AC и \(\angle3=\angle4\) верны (по равенству треугольников). Ч.Т.Д.
Касательная перпендикулярна радиусу, проведенному в точку касания.
Доказательство
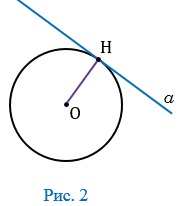
Дано: a — касательная к кругу с центром O. Она пересекает круг в точке H.
Доказать: \(OH\perp a\).
Доказательство: воспользуемся методом от противного. Предположим, что OH не перпендикулярна a. В этом случае радиус OH — наклонная к прямой a. Перпендикуляр, проведенный из точки O к a, меньше наклонной OH. Тогда расстояние от центра O до прямой a меньше радиуса. Значит, у прямой a и окружности есть две общие точки, что противоречит условию, в котором прямая a — касательная. Следовательно, предположение неверно и \(H\perp a\). Ч.Т.Д.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так