Основные действия над комплексными числами

Комплексные числа — определение и основные понятия

Обычные числа представляют собой множество действительных чисел, для обозначения которых используют букву R. Каждое число из множества можно отметить на числовой прямой.

К действительным числам носят:

• целые числа;
• дроби;
• иррациональные числа.

Каждая точка на числовой прямой характеризуется некоторым действительным числом. Комплексное число является двумерным числом и записано в виде:

z = a + bi

Где а и b являются действительными числами, i представляет собой так называемую мнимую единицу.

Уравнение можно мысленно поделить на несколько частей:

• a — действительная часть (Re z) комплексного числа z;
• b — мнимая часть (Im z) комплексного числа z.

Следует отметить, что a + bi является единым числом, а не сложением. Места действительной и мнимой частей в уравнении можно менять:

z = bi + a

Мнимую единицу допускается переставлять:

z = a + ib

При таких операциях смысл выражения остается прежним. Однако стандартная запись комплексного числа имеет такой вид:

z = a + bi

Данное утверждение можно привести в виде геометрической интерпретации. Тогда комплексные числа изображают на комплексной плоскости.

С помощью R обозначаю множество действительных чисел. В случае, когда требуется обозначить множество комплексных чисел, принято использовать букву С. Наличие буквы С на чертеже говорит о том, что на нем представлена комплексная плоскость. Данная плоскость включает две оси:

Re z — является действительной осью;

Im z — представляет собой мнимую ось.

Правила оформления такого графика практически не отличаются от требований к чертежам для декартовой системы координат. По осям задают масштаб и отмечают:

• ноль;
• единицу для действительной оси;
• мнимую единицу i для мнимо оси.

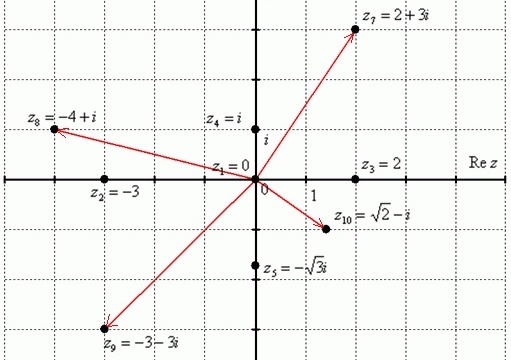
С помощью комплексной плоскости можно построить заданные комплексные числа:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

\(z_{4}=i\)

\(z_{5}=-\sqrt{3}i\)

\(z_{6}=4i\)

\(z_{7}=2+3i\)

\(z_{8}=-4+i\)

\(z_{9}=-3-3i\)

\(z_{5}=-\sqrt{2}-i\)

Можно рассмотреть следующие комплексные числа:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

Действительные числа являются частным случаем комплексных чисел. Действительная ось Re z обозначает в точности множество действительных чисел R, то есть на данной оси расположены все числа с обычными свойствами. Можно сформулировать справедливое утверждение: множество действительных чисел R представляет собой подмножество множества комплексных чисел С.

Данные числа являются комплексными числами, мнимая часть которых нулевая:

\(z_{1}=0\)

\(z_{2}=-3\)

\(z_{3}=2\)

Мнимые числа с нулевой действительностью, которые расположены на мнимой оси Im z:

\(z_{4}=i\)

\(z_{5}=-\sqrt{3}i\)

\(z_{6}=4i\)

Есть ряд чисел с ненулевыми действительной и мнимой частью:

\(z_{7}=2+3i\)

\(z_{8}=-4+i\)

\(z_{9}=-3-3i\)

\(z_{5}=-\sqrt{2}-i\)

Для их обозначения используют точки на комплексной плоскости. К таким точкам проводят радиус-векторы из начала координат. Радиус-векторы не принято чертить к числам, которые расположены на осях и сливаются с ними.

Формы, как записываются

Алгебраическая запись комплексного числа имеет такой вид:

z = a + bi.

Кроме данной формы существует еще несколько способов для записи. Удобным и наглядным геометрическим представлением является:

z = a + bi в виде вектора с координатами (а;b) на декартовой плоскости, либо точкой — концом вектора с аналогичными координатами.

В этом случае пару комплексных чисел представляют в виде суммы соответствующих векторов, которую рассчитывают с помощью правила параллелограмма. Согласно теореме Пифагора, длина вектора с координатами (а;b) определяется, как:

\(\sqrt{a^{2}+b^{2}}\)

Данная величина представляет собой модуль комплексного числа z = a + bi и имеет такое решение:

\(\left|z \right|\)

Вектор и положительное направление оси абсцисс образуют угол, отсчитанный против часовой стрелки. Данный угол называют аргументом комплексного числа z и обозначают, как Arg z. Аргумент имеет неоднозначное определение с точностью до прибавления величины, которая кратна 2π радиан. При повороте на такой угол вокруг начала координат вектор не изменяется.

В том случае, когда вектор длиной r с положительным направлением оси абсцисс составляет угол ϕ, его координаты будут следующими:

\(\left(r*\cos \varphi ;r*\sin \varphi \right)\)

Таким образом, получают тригонометрическую форму записи комплексного числа:

\(z=\left|z \right|*\left(\cos (Arg z)+i\sin (Arg z) \right)\)

Из-за более простого вида вкладок комплексные числа, как правило, представляют в тригонометрической форме.

Существует показательная форма для записи комплексных чисел. Какое-либо комплексное число, не равное нулю, можно представить в показательной форме:

\(z=\left|z \right|*e^{i\varphi }\)

Где \(\left|z \right|\)является модулем комплексного числа,

\(\varphi\) представляет собой аргумент комплексного числа.

Представить комплексное число в показательной форме можно с помощью нескольких действий:

• изобразить чертеж;
• найти модуль;
• рассчитать аргумент.

Основные действия над комплексными числами с примерами

Манипуляции с комплексными числами выполняют так же, как с действительными числами. Арифметические действия могут быть следующими:

• сложение;
• вычитание;
• умножение;
• деление.

Складывать и вычитать комплексные числа можно с помощью правила:

(a + bi) ± (c + di) = (a ± c) + (b ± d)i

Умножение комплексных чисел выполняют таким образом:

(a + bi) · (c + di) = (ac – bd) + (ad + bc)i 

В данном случае \(i^{2}=-1\)

Число \(\bar{z}=a-bi\) является комплексно-сопряженным к \(z=a+bi\)

С помощью равенства \(z*\bar{z}=a^{2}+b^{2}\) можно установить, как делить одно комплексное число на другое, не равное нулю, комплексное число:

\(\frac{a+bi}{c+di}=\frac{(a+bi)*(c-di)}{(c+di)*(c-di)}=\frac{(ac+bd)+(bc-ad)i}{c^{2}+d^{2}}=\frac{ac+bd}{c^{2}+d^{2}}+\frac{bc-ad}{c^{2}+d^{2}}i\)

Пример:

\(\frac{3+4i}{1+2i}=\frac{11}{5}-\frac{2}{5}i\)

Сложение комплексных чисел

Ели требуется сложить пару комплексных чисел:

\(z_{1}=1+3i\)

\(z_{2}=4-5i\)

Сначала нужно найти сумму их действительных и мнимых частей:

\(z_{1}+ z_{2}=1+3i+4-5i=5-2i\)

Таким образом, сумма какого-либо количества слагаемых определяется путем сложения действительных частей и сложением мнимых частей. В случае комплексных чисел справедливо правило первого класса, которое гласит, что от перестановки слагаемых их сумма остается прежней:

\(z_{1}+ z_{2}= z_{2}+ z_{1}\)

Вычитание комплексных чисел

Разность комплексных чисел:

\(z_{1}- z_{2}\)

\(z_{2}- z_{1}\)

При условии, что:

\(z_{1}=-2+i\)

\(z_{2}=\sqrt{3}+5i\)

Действие аналогично сложению. Разница заключается в необходимости выделения скобками вычитаемого числа. Далее следует раскрыть скобки и изменить знак:

\(z_{1}- z_{2}=-2+i-(\sqrt{3}+5i )=-2+i-\sqrt{3}-5i =-2-\sqrt{3}-4i \)

Полученное в результате число обладает двумя частями. Действительная часть является составной:

\(-2-\sqrt{3}\)

Наглядно ответ будет записан в такой форме:

\(z_{1}- z_{2}=(-2-\sqrt{3})-4i \)

Умножение комплексных чисел

Можно найти произведение комплексных чисел:

\(z_{1}=1-i\)

\(z_{2}=3+6i\)

Произведение будет записано таким образом:

\(z_{1}* z_{2}=(1-i)(3+6i)\)

Раскрыть скобки следует, руководствуясь правилом умножения многочленов, учитывая, что \(i^{2}=-1\)

Для того чтобы перемножить многочлены, требуется каждый член одного многочлена умножить на каждый член другого многочлена. Таким образом:

\(z_{1}* z_{2}=(1-i)(3+6i)=1*3-i*3+1*6i=3-3i+6i+6=9+3i\)

\(-i*6i=-6i^{2}=-6*(-1)=+6\)

Как и в случае со сложением, произведение комплексных чисел перестановочно, то есть справедливо равенство:

\(z_{1}* z_{2}= z_{2}* z_{1}\)

Деление комплексных чисел

На примере комплексных чисел:

\(z_{1}=13+i\)

\(z_{2}=7-6i\)

требуется определить частное:

\(\frac{z_{1}}{z_{2}}\)

Частное будет записано в таком виде:

\(\frac{z_{1}}{z_{2}}=\frac{13+i }{7-6i }=\)

Делить числа необходимо с помощью метода умножения знаменателя и числителя на сопряженное знаменателю выражение. В этом случае пригодится стандартная формула:

\((a-b)(a+b)=a^{2}-b^{2}\)

По условию знаменатель 7-6i. В данном знаменателе уже есть (а-b), поэтому сопряженным выражением в таком случае является (a+b), то есть 7+6i. Исходя из правила, знаменатель умножают на 7+6i. Сохранить равенство можно с помощью умножения числителя на то же самое число 7+6i:

\(\frac{z_{1}}{z_{2}}=\frac{(13+i)(7+6i)}{(7-6i)(7+6i)}\)

Затем в числителе необходимо раскрыть скобки, то есть умножить пару чисел, согласно отмеченному ранее правилу. Для знаменателя требуется использовать формулу \((a-b)(a+b)=a^{2}-b^{2}\) и \(i^{2}=-1\)

Уравнение будет записано в таком виде:

\(\frac{z_{1}}{z_{2}}=\frac{(13+i)(7+6i)}{(7-6i)(7+6i)}=\frac{91+7i+78i+6i^{2}}{7^{2}-(6i)^{2}}=\frac{91+7i+78i-6}{49-(-36)}=\frac{85+85i}{49+36}=\frac{85+85i}{85}=1+i\)

Нахождение аргумента

При выполнении действий с модулем комплексных чисел необходимо руководствоваться формулой:

\(\left|z \right|=\sqrt{a^{2}+b^{2}}\)

Для поиска аргумента комплексного числа требуется использовать определенную формулу для конкретного случая. Уравнение подбирается, исходя из положения числа z = a + bi в координатной четверти. Существует всего три таких варианта:

• а > 0, число соответствует первой и четвертой координатной четверти, либо правой полуплоскости, формула для нахождения аргумента \(Arg z=arctg\frac{b}{a}\);
• a < 0, b > 0, число соответствует второй координатной четверти, формула для расчета аргумента\(Arg z=\pi +arctg\frac{b}{a}\);
• a < 0, b < 0, число соответствует третьей координатной четверти, найти аргумент можно по формуле \(Arg z=-\pi +arctg\frac{b}{a}\).

Извлечение корня из комплексных чисел

Комплексные числа в тригонометрической форме умножают таким образом:

z_{1}*z_{2}=\left|z_{1} \right|*\left|z_{2} \right|*(\cos (Arg z_{1}+Arg z_{2})+i\sin (Arg z_{1}+Arg z_{2}))2

При умножении пары комплексных чисел их модули перемножаются, а аргументы складываются. Исходя из этого утверждения, вытекают формулы Муавра:

\(z^{n}=\left|z\right|^{n}*(\cos (n*(Arg z))+i\sin (n*(Arg z)))$\)

С помощью этого равенства можно извлечь корни любой степени из комплексных чисел. Корень n-й степени из числа z представляет собой комплексное число w, которое:

\(w^{n}=z\)

Заметим, что:

\(\left|w \right|=\sqrt[n]{\left|z \right|}\)

Тогда:

\(Arg w=\frac{1}{n}Arg z+\frac{2\pi k}{n}\)

Где k может обладать любым значением из множества (0, 1, …, n-1).

Таким образом, в любом случае имеется ровно n корней n-ой степени из комплексного числа. На плоскости все они будут расположены в вершинах правильного n-угольника.

Возведение комплексных чисел в степень

В качестве примера можно возвести в квадрат комплексное число:

z = 2 + 3i

Первый способ заключается в записи степени в виде произведения множителей:

\(z^{2}=(2+3i)^{2}=(2+3i)(2+3i)\)

Далее необходимо перемножить числа, согласно правилу умножения многочленов.

Второй метод заключается в использовании уравнения для сокращенного умножения:

\((a+b)^{2}=a^{2}+2ab+b^{2}\)

Выражение примет следующий вид:

\(z^{2}=(2+3i)^{2}=2^{2}+2*2*3i+(3i)^{2}=4+12i-9=-5+12i\)

В случае комплексного числа можно достаточно просто записать определенную формулу для сокращенного умножения:

\((a+bi)^{2}=a^{2}+2abi+(bi)^{2}=a^{2}+2abi-b^{2}\)

Такую же формулу можно представить для расчета квадрата разности, куба суммы и куба разности. Если необходимо возвести в 5-ю, 10-ю или любую другую степень комплексное число, следует воспользоваться тригонометрической формой комплексного числа, то есть формулу Муавра. К примеру, дано комплексное число в тригонометрической форме:

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}z=\left|z \right|*\left(\cos \varphi +i\sin \varphi \right)\)

Данное число требуется возвести в натуральную степень n. Для этого необходимо использовать уравнение:

\(z^{n}=\left|z \right|^{n}*\left(\cos (n\varphi) +i\sin (n\varphi) \right)\)

Представленная формула вытекает из правила для умножения комплексных чисел, которые записаны в тригонометрической форме. Для того чтобы найти произведение чисел, требуется:

\(z_{1}=\left|z_{1} \right|*(\cos \varphi _{1}+i\sin \varphi _{1})\)

\(z_{2}=\left|z_{2} \right|*(\cos \varphi _{2}+i\sin \varphi _{2})\)

Далее требуется перемножить модули этих комплексных чисел и найти сумму аргументов:

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}z_{1}* z_{2}=\left|z_{1} \right|*\left|z_{2} \right|*(\cos( \varphi _{1}+\varphi _{2})+i\sin ( \varphi _{1}+\varphi _{2})\)

Аналогичный порядок действий для показательной формы комплексного числа:

\(z_{1}=\left|z_{1} \right|*e^{i\varphi _{1}}\)

\(z_{2}=\left|z_{2} \right|*e^{i\varphi _{2}}\)

Таким образом:

\(z_{1}*z_{2}=\left|z_{1} \right|*\left|z_{2} \right|*e^{i(\varphi _{1}+\varphi _{2})}\)