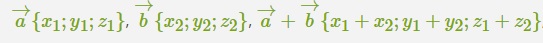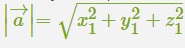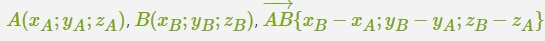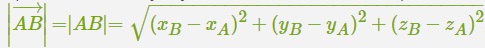Способы вычисления координат вектора
Что такое координаты вектора — какие операции можно производить
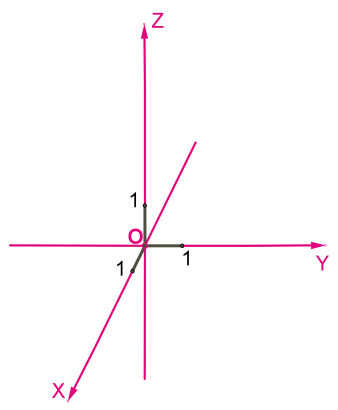
Три попарно перпендикулярные прямые с определенными направлениями и единицей измерения в геометрии составляют систему координат в пространстве. Точка, в которой пересекаются данные прямые, представляет собой начало координат.
Оси координат:
- \(Ox\) — ось абсцисс.
- \(Oy\) — ось ординат.
- \(Oz\) — ось аппликат.
Через две прямые, которые пересекаются, можно построить плоскость. Таким образом, образуются три координатные плоскости в виде:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- \((Oxy)\);
- \((Oyz)\);
- \((Oxz)\).
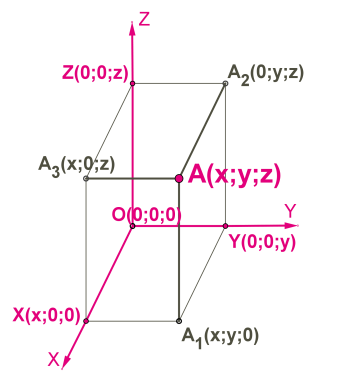
Определить положение точки \(А\) в пространстве можно с помощью трех координат \(x, y\) и \(z\).
Координата x является понятием абсциссы точки \(A\), координата y — определяет ординату точки \(A\), координата \(z\) — аппликату точки \(A\).
Запись имеет следующий вид:
\(A(x;y;z)\).
Варианты расположения точки:
- в том случае, когда точка расположена на оси \(Ox\), ее координаты — \(X(x;0;0)\);
- при нахождении точки на оси \(Oy\) она характеризуется координатами \(Y(0;y;0)\);
- если точка принадлежит оси \(Oz\), ее координаты — \(Z(0;0;z)\);
- точка, лежащая в плоскости \(Oxy\), обладает координатами \(A1(x;y;0)\);
- в том случае, когда расположение точки совпадает с плоскостью \(Oyz,\) она обладает координатами \(A2(0;y;z)\);
- если точка расположена в плоскости \(Oxz\), то данная точка имеет координаты \( A3(x;0;z)\).
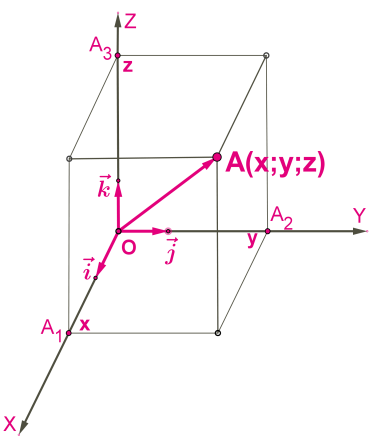
Допустим, что в системе координат существуют некие единичные векторы \(\overrightarrow { i }\), \(\overrightarrow { j }\) и \(\overrightarrow { k }\), которые были отложены от начала координат. В этом случае допустимо определить прямоугольный базис. Какой-либо вектор раскладывается на единичные вектора и записывается в виде:
\(\overrightarrow {OA}=x⋅\overrightarrow { i }+y⋅\overrightarrow { j }+z⋅\overrightarrow { k }\)
Коэффициенты \(x\), \(y\) и \( z\) могут иметь одно единственное значение и являются координатами вектора.
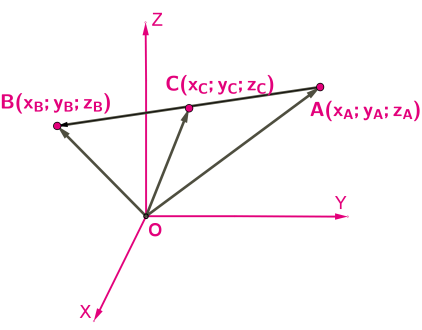
В прямоугольной системе координат \(Х0у\) проекции х и у вектора \(\overrightarrow {OA}\) на оси абсцисс и ординат называют координатами вектора. То есть координаты вектора являются числами, описывающими положение вектора относительно координатной плоскости.
Координатами вектора, начало которого совпадает с точкой \(A(x1; y1)\), а конец — соответствует точке \(B(x2; y2)\), называют числа:
\(a1 = x2 — x1\);
\(a2 = y2 — y1\).
Координаты вектора записывают в таком виде:
\(\overrightarrow {OA}{x;y;z}\).
Правила записи с помощью координат:
Координаты суммы векторов при наличии известных координат векторов:
Координаты разности векторов при заданных координатах векторов:
Координаты произведения вектора на число при наличии определенных координатах вектора:
Длина, которой обладает вектор:
Координаты вектора при заданных координатах, которыми характеризуются начальная и конечная точки вектора:
Расстояние по модулю, на которое удалены две точки с заданными координатами:
Координаты серединной точки отрезка, когда заданы координаты начальной и конечной точек отрезка:
Координаты вектора обладают следующими свойствами:
- Какие-либо равные векторы в единой системе координат обладают идентичными координатами.
- Координаты коллинеарных векторов пропорциональны в том случае, когда ни один из векторов не обладает нулевым значением.
- Квадрат длины какого-либо вектора определяется как сумма квадратов его координат.
- В процессе умножения вектора на действительное число каждая его координата умножается на это число.
- Когда требуется сложить вектора, следует определить сумму соответствующих координат данных векторов.
- Скалярное произведение пары векторов соответствует сумме произведений их соответствующих координат.
Способы представления, как записываются
Общепринятой является запись координат вектора в виде:
\((х, у)\).
Непосредственно вектор обозначают, как:
\(\overrightarrow {AB} =(х, у)\).
Координаты вектора записывают в круглых скобках рядом с буквенным обозначением вектора:
\(\overrightarrow {AB} (a_1 ;a_2 )\)
или
\(\overrightarrow a (a_1 ;a_2 )\)
В некоторых случаях допустимо использовать запись координат вектора без буквенного обозначения, то есть со знаком вектора над скобками:
\(\overrightarrow {(a_1 ;a_2 )}\)
Нулевой вектор обладает нулевыми координатами:
\(\overrightarrow 0 (0;0)\)
Методы вычисления координат вектора
В том случае, когда определены координаты начала и конца вектора \(\overline{AB}:\ A\left(x_{1} ;\; y_{1} \right),\; B\left(x_{2} ;\; y_{2} \right)\), при вычислении его координат требуется от координат конца отнять соответствующие координаты начала:
\(\overline{AB}=\left(x_{2} -x_{1} ;\; y_{2} -y_{1} \right)\)
Формула определения координат вектора для двухмерных задач: в рассматриваемом случае вектор \( \overline{AB} \)с заданными координатами точек \(A(х1;у1) и B(x2;y2)\) можно найти по формуле:
\(\overline{AB}=(x2 – x1 ; y2 – y1).\)
Формула определения координат вектора для пространственных задач: если требуется решить пространственную задачу на нахождение вектора \(\overline{AB}\), координаты точек \(A(х1;у1;z1) и B(x2;y2;z2)\) которого известны, следует воспользоваться формулой:
\(\overline{AB}=(x2 – x1 ; y2 – y1; z2 – z1)\)
С помощью вычисления координат вектора можно определить его характеристики, в том числе найти длину вектора. Зная координаты, достаточно просто построить вектор.
Примеры задачи на нахождение координат вектора
Существуют пары точек:
\(A(-3; 7), B(2; -1)\);
\(С(5; 0), D(11; 8). \)
Необходимо определить координаты векторов:
\(\overrightarrow {AB} ,\overrightarrow {CD} .\)
Решение:
С целью вычисления координат вектора необходимо из координат его конца (точки B) вычесть координаты начала (точки A):
\(\overrightarrow {AB} (2 - ( - 3); - 1 - 7)\)
\(\overrightarrow {AB} (5; - 8).\)
Аналогичным способом можно рассчитать координаты второго вектора:
\(\overrightarrow {CD} (11 - 5;8 - 0)\)
\(\overrightarrow {CD} (6;8)\)
Ответ: \(\overrightarrow {AB} (5; - 8); \overrightarrow {CD} (6;8).\)
Требуется вычислить координаты вектора \(\overline{AB}\) при условии, что:
\(A\left(-1;\; 2\right),\ B\left(2;\; -3\right)\)
Решение
Определить координаты, которым характеризуется вектор \(\overline{AB}\), исходя из известных по заданию координат его начальной точки \(A\left(-1;\; 2\right)\) и конечной точки \(B\left(2;\; -3\right)\), можно путем вычитания из координат конечной точки соответствующих координат начальной точки. Таким образом, первым и единственным действием в данном случае является:
\(\overline{AB}=\left(2-\left(-1\right)\, ;\; -3-2\right)=\left(3;\; -5\right)\)
Ответ: \(\overline{AB}=\left(3;\; -5\right)\)
Необходимо определить координаты точки \(A\), которая представляет собой начало вектора \(\overline{AB}=\left(0;\; -4;\; 3\right)\), а концом вектора является точка \(B\left(-1;\; 6;\; 1\right).\)
Решение
Предположим, что точка \(A \) обладает следующими координатами:
\(A\left(a_{1} ;\; a_{2} ;\; a_{3} \right)\)
В таком случае, вектор \(\overline{AB}\), при условии, что точка \(B\left(-1;\; 6;\; 1\right)\), характеризуется следующими координатами:
\(\overline{AB}=\left(-1-a_{1} ;\; 6-a_{2} ;\; 1-a_{3} \right)=\left(0;\; -4;\; 3\right)\)
Зная, что равенство двух векторов достигается при равенстве соответствующих координат этих векторов, можно записать следующие уравнения для вычисления неизвестных координат, которыми характеризуется точка \(А\):
\(-1-a_{1} =0\Rightarrow a_{1} =-1\)
\(6-a_{2} =-4\Rightarrow a_{2} =10\)
\(1-a_{3} =3\Rightarrow a_{3} =-2\)
В результате:
\(A\left(-1;\; 10;\; -2\right)\)
Ответ: \(A\left(-1;\; 10;\; -2\right)\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так