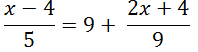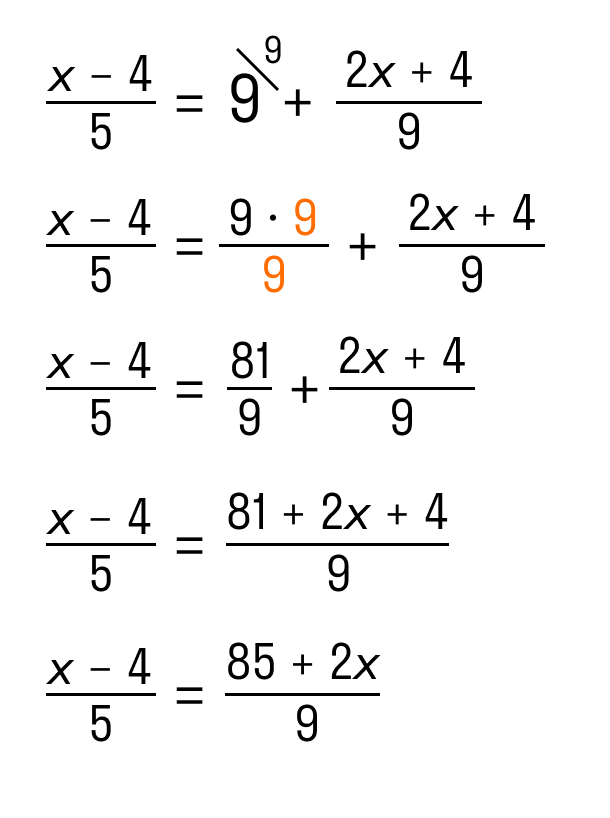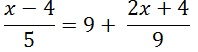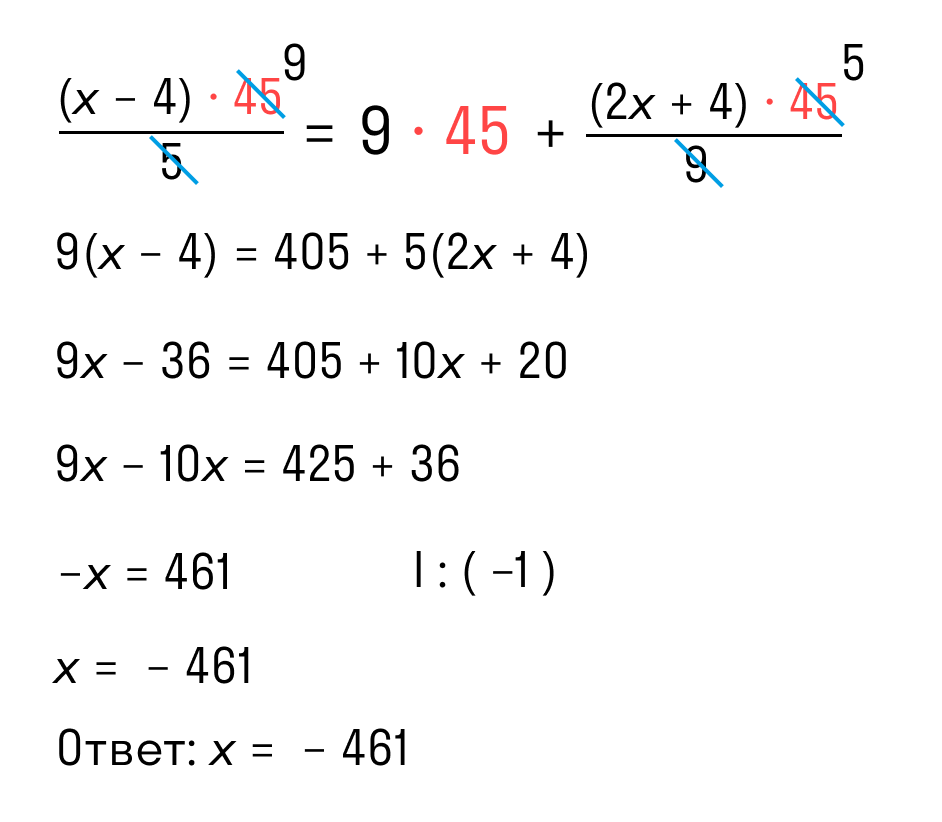Линейное уравнение с одной переменной

Что такое линейное уравнение с одной переменной

Рассмотреть понятие линейного уравнения можно на образце задачи. Предположим, что нужно определить такие численные значения переменной х, при которых соответственные значения выражений 3х и х+8 будут одинаковыми. Для этого необходимо решить уравнение:

3х=х+8

Если х=4, правая и левая части уравнения будут равны. В данном случае число 4 является решением или корнем рассматриваемого уравнения.

Решить уравнение в алгебре — значит определить множество всех его корней.

Линейным уравнением является любое алгебраическое уравнение, обладающее одним неизвестным, степень которого равна единице.

Общий вид линейного уравнения можно записать, таким образом:

kx+b=0

Где k и b — являются произвольными числами.

Примеры линейных уравнений:

1. Уравнение x+5=8 обладает одним корнем 3. Уникальность корня объясняется тем, что при x<3 левая часть уравнения будет меньше 8, а при x>3 больше 8.
2. Уравнение (x+2)(x-1)(x-7)=0 включает три корня: -2, 1 и 7. Каждый корень при подстановке в выражение превращает его в справедливое равенство. Когда х равен любому другому числу, ни один из множителей (а значит, и их произведение) не равен нулю.
3. Уравнение x+3=x-1 не обладает корнями, так как при любых x значение выражения, стоящего в левой части уравнения, на 4 больше соответственного значения выражения, которое расположено в правой части. Множество корней будет пустым.
4. Уравнение x=|x| обладает бесконечным множеством корней. Какое-либо число, больше нуля, или ноль может стать его корнем.
5. Уравнение 5(x+8)=40+5x обладает бесконечным множеством корней. При этом любое значение х — корень уравнения, в связи с тем, что выражения 5(x+8) и 40+5x тождественно равны. Данное уравнение удовлетворяется тождественно.

Перечисленные уравнения обладают общей формой:

\(kx+b=0 \Leftrightarrow kx=-b\)

Рассматриваемые выражения по внешнему виду схожи друг с другом. Значение х является переменной или неизвестным, k и b — представляют собой произвольные числа.

Уравнения, которые не соответствуют этой записи, не являются линейными, к примеру:

\(x^{2}-1=0\)

(x-3)(x+5)=0

\(\left | x \right |=2\)

Свойства, алгоритм вычислений, основные принципы

При решении задач с линейными уравнениями целесообразно воспользоваться определенными закономерностями. 

К примеру:

\(x+2=0 \Rightarrow x=-2\)

Необходимость в смене знака объясняется тем, что к обоим частям уравнения можно прибавить одинаковое число. При этом равенство остается справедливым:

x+2+(-2)=0+(-2)

\(x+0=0-2 \Rightarrow x=-2\)

К примеру, можно умножить обе части выражения на 4 и получить следующее равенство:

\(x+2=0 \Rightarrow (x+2)\cdot 4=0\cdot 4\)

4x+8=0

В математике существует понятие равносильных уравнений. Можно рассмотреть подобные равенства на примере:

• (x+2)(x-3)=0
• x(x+2)(x-3)=0

В данном случае первое уравнение обладает двумя корнями: -2 и 3, а второе — тремя корнями: 0, -2 и 3. Любой корень первого уравнения представляет собой и корень второго уравнения. Однако не каждый корень второго уравнения будет определен, как корень первого уравнения. Если x=0 второе уравнение будет являться верным равенством, а первое — нет.

Уравнение x(x+2)=3(x+2) обладает двумя корнями: -2 и 3. Любое решение третьего уравнения будет также являться решением первого уравнения. Каждое из решений первого уравнения соответствует решению третьего уравнения. Таким образом, первое и третье уравнения будут называть равносильными.

Определение 

Равносильными называют уравнения, у которых множества решений совпадают.

Рассмотреть свойства равенств удобно на примере двух уравнений: 2x-5=9 и 2x=14. Определить, равносильны ли они, можно с помощью следующих свойств:

1. Рефлексивность. Каждое число равно самому себе, то есть а=а.
2. Симметричность. В том случае, когда одно число равно второму, то второе число также будет равно первому, то есть, если а=b, то b=а.
3. Транзитивность. В том случае, когда первое число равно второму, а второе обладает таким же значением, как и третье, то первое число будет равно третьему: a=b и b=c, то a=c.
4. При сложении обеих частей справедливого равенства с одним и тем же числом в результате получится верное равенство, то есть если a=b, то a+c=b+c.
5. При умножении обеих частей справедливого равенства на одно и то же число результатом будет являться верное равенство: если a=b, то \(a\cdot c=b\cdot c\).

Решение линейных уравнений с применением свойств равенств можно разобрать на конкретных примерах.

Задача 1

Требуется найти решение уравнения:

6x-42=0

Решение:

В первую очередь следует сложить левую и правую части уравнения с числом 42. Таким образом, будет осуществлен перенос числа -42 в правую часть равенства с противоположным знаком. В результате уравнение приобретает следующий вид:

6x=42

В том случае, когда при каком-то значении х равенство справедливо, то верным будет и то равенство, которое было записано. Наоборот, когда имеется некоторое значение х, записанное равенство справедливо, то исходное равенство также будет верным. Данный факт является следствием рассмотренных свойств равенств. Таким образом, можно говорить о равнозначности уравнений:

\(6x-42=0\Leftrightarrow6x=42\)

Далее следует умножить все части уравнения на:

\(\frac{1}{6} \)

Получим:

x=7

Исходя из свойства равенств, можно сделать вывод о равнозначности последних двух уравнений:

\(6x=42 \Leftrightarrow x=7\)

Таким образом, согласно свойству транзитивности равносильных уравнений, можно считать равносильными и данные уравнения:

\(6x-42=0 \Leftrightarrow x=7\)

Получается, что 7 является корнем исходного уравнения.

Ответ: х=7.

С помощью данного примера можно заключить, что при переносе элементов равенства из одной части в другую с противоположным знаком и умножении, либо делении обеих частей уравнения на число, которое отлично от нуля, получается уравнение, равносильное данному.

Задача 2

Необходимо найти решение уравнения:

\(\frac{3}{4}x-\frac{5x}{16}=2\)

Решение

В первую очередь следует привести все слагаемые левой части равенства к общему знаменателю:

\(\frac{3x}{4}\cdot\frac{4}{4}-\frac{5x}{16}=2\)

\(\frac{12x}{16}-\frac{5x}{16}=2\)

\(\frac{12x-5x}{16}=2\)

\(\frac{7x}{16}=2\)

Далее можно умножить каждую часть уравнения на:

\(\frac{16}{7}\)

После того, как исключен коэффициент при неизвестном, получим:

\(\frac{7x}{16}\cdot\frac{16}{7}=2\cdot\frac{16}{7}\)

В данном случае допустимо сократить числа 7 и 16, что в результате позволит получить равенство:

\(x=\frac{32}{7}\)

Ответ: \(x=\frac{32}{7}\)

Подытожив рассмотренные примеры, можно записать алгоритм решения линейных уравнений с одним неизвестным:

kx+b=0

Решение определяется параметрами k и b. Исходя из этого, можно предложить несколько вариантов решений.

Вариант 1, при котором коэффициент при неизвестной k имеет нулевое значение, а свободный член b не равен нулю:

\(k=0, b\neq 0 \Rightarrow 0\cdot x=-b\)

В таком случае, не получится определить такое число х, которое, находясь в уравнении, преобразует его в справедливое равенство. Это связано с тем, что при умножении на 0 получится результат с нулевым значением. Таким образом, можно сделать вывод об отсутствии решений, что следует записать, как «х принадлежит пустому множеству»:

\(x\in \oslash\)

Вариант 2, при котором значения коэффициента при неизвестной и свободный член не равны нулю:

\(k\neq 0, b\neq 0 \Rightarrow kx=-b \Rightarrow x=\frac{-b}{k}\)

Таким образом, х будет являться действительным и единственным решением в форме отношения пары чисел: -b и k.

Вариант 3, при котором k и b равны нулю, то есть:

\(k=0, b=0 \Rightarrow kx=-b \Rightarrow 0\cdot x=0\)

При любом х равенство будет справедливым. Это связано с тем, что, если число умножить на 0, получится 0. В этом случае, х является любым числом, либо принадлежит множеству всех действительных чисел, что можно записать, таким образом:

\(x\in \mathbb{R}\)

Существует несколько способов записи решения. К примеру, можно воспользоваться двойным неравенством:

\(-\infty <x< \infty\)

Данная формулировка означает, что х является числом из промежутка от минус бесконечности до плюс бесконечности. Так как бесконечность не является числом, неравенство будет строгим. Ответ можно представить, как интервал:

\(x\in(-\infty;\infty)\)

Знак \(\in \)справедливо заменить словом «принадлежит». Такой символ носит название квантора принадлежности. В этом случае формулировка будет следующей: «х принадлежит любому числу из данного интервала».

Исходя из того, что решение линейного уравнения — это корень уравнения. Следовательно, при решении линейного уравнения необходимо привести его к виду:

x=…

Виды уравнений с одной переменной

Существуют разные алгебраические уравнения. Наиболее распространенными из них являются:

• линейные;
• квадратные.

Линейные уравнения записывают в виде:

ах + b = 0

Где a и b — являются действительными числами.

В решении линейных уравнений удобно применять следующие свойства:        

• в том случае, когда а не равно нулю, уравнение обладает единственным корнем: х = -b : а;
• при нулевом значении, а уравнение не имеет корней;
• когда а и b равны нулю, корень уравнения является любым числом.

Квадратное уравнение имеет следующий вид:

ax² + bx + c = 0,

Где коэффициенты a, b и c — являются произвольными числами, a обладает ненулевым значением.          

Решение уравнений (алгоритм сведения уравнений к линейным)

Решить многие уравнения можно путем их сведения к линейным. Существует несколько действенных способов. Алгоритм действий может отличаться в зависимости от вида уравнения.

Графический способ решения уравнений с одной переменной

Решить уравнения с одной переменной можно графическим методом. Стандартный алгоритм включает несколько шагов:

• выразить\( \displaystyle x\) с помощью \(\displaystyle y\);
• определить, к какому типу относится функция;
• построить графики получившихся функций;
• найти точки, в которых пересекаются графики;
• записать корректный ответ, учитывая ОДЗ и знаки неравенств;
• проверить ответ, то есть подставить корни в уравнение или систему.

Графическое решение линейных уравнений

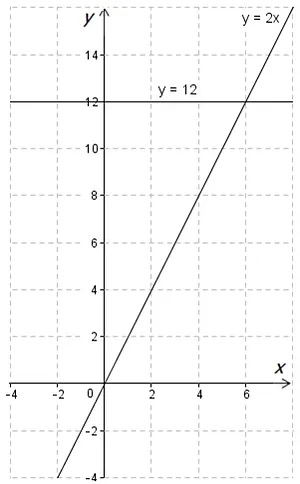
График линейного уравнения представляет собой прямую линию. Разобрать данный способ удобно на конкретном примере. Требуется решить уравнение:

\(\displaystyle 2{x} -10=2\)

Способ 1 заключается в переносе неизвестных в одну сторону, а известных — в другую. Таким образом:

\(\displaystyle 2x=2+10\)

\(\displaystyle 2x=12\)

Далее необходимо поделить правую часть уравнения на левую, чтобы получить искомый корень. Однако можно пойти другим путем и представить обе части уравнения в виде различных функций в одной системе координат:

\(\displaystyle {{y}_{1}}=2x\)

\(\displaystyle {{y}_{2}}=12\)

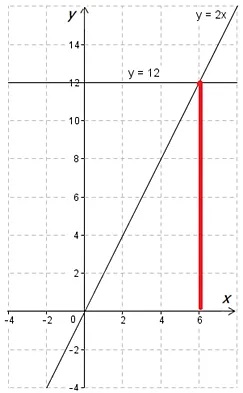
График будет иметь следующий вид:

В данном случае координата \(\displaystyle x\) точки пересечения графиков является корнем уравнения:

Ответ: \(\displaystyle x=6\)

Полученный корень уравнения следует проверить, подставив его в уравнение.

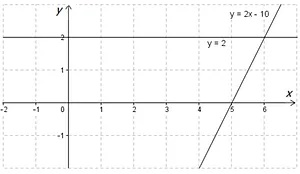
Способ 2 не предусматривает перенос элементов уравнения, а заключается в том, что графики строят напрямую. Дано уравнение:

\(\displaystyle 2{x} -10=2\)

Построим графики:

\(\displaystyle {{y}_{1}}=2{x} -10\)

\(\displaystyle {{y}_{2}}=2\)

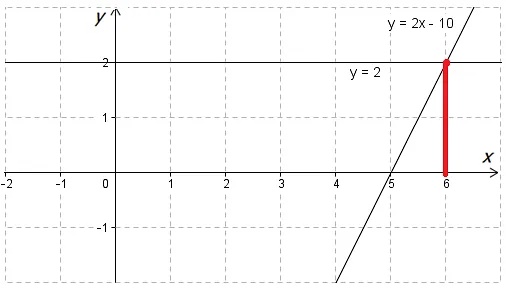
В данном случае решением будет та же координата \(\displaystyle x\) точки пересечения графиков, которая была получена в решении уравнения первым способом:

Ответ: \(\displaystyle x=6\)

Графическое решение квадратных уравнений

Графическим методом можно решать квадратные уравнения. К примеру, дано уравнение, корни которого необходимо найти:

\(\displaystyle {{x}^{2}}+2{x} -8=0\)

Способ 1 позволяет решить уравнение напрямую. Для этого необходимо построить параболу, согласно уравнению:

\(\displaystyle {{x}^{2}}+2{x} -8=0\)

Как правило, начинают строить график после определения вершины параболы. Определить ее координаты можно, таким образом:

\(\displaystyle x=-\frac{b}{2a}\)
\(\displaystyle y=-\frac{{{b}^{2}}-4ac}{4a}\)

Получилось следующее:

\(\displaystyle x=\frac{-2}{2}=-1\)
\(\displaystyle y=-\frac{{{2}^{2}}-4\cdot \left( -8 \right)}{4}=-\frac{4+32}{4}=-9\)

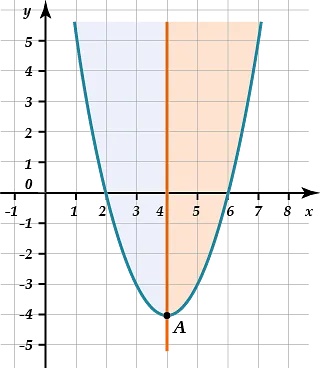
Далее нужно построить точки в количестве от \(\displaystyle 3\). Парабола симметрична относительно своей вершины. К примеру:

Таким образом, нужно построить еще пару точек слева и справа по ветвям параболы. Далее эти точки необходимо симметрично отразить на противоположную сторону:

Получена точка \(\displaystyle A\left( -1;-9 \right)\). Требуется еще пара точек. Целесообразно взять положительные. Можно выполнить расчет при \(\displaystyle x=0\) и \(\displaystyle x=2\).

При \(\displaystyle x=0:\)

\(\displaystyle y={{0}^{2}}+0-8=-8\)

При \(\displaystyle x=2:\)

\(\displaystyle y={{2}^{2}}+2\cdot 2-8=0\)

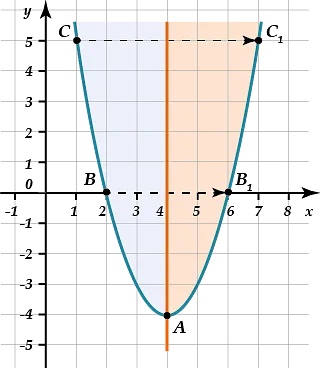
Получив три точки, можно построить параболу, отразив две последние точки относительно ее вершины:

Решением уравнения будут точки, в которых \(\displaystyle y=0\). Таким образом, \(\displaystyle x=2\) и \(\displaystyle x=-4\) представляют собой корни уравнения, так как  \({{x}^{2}}+2{x} -8=0\). В том случае, когда \(y={{x}^{2}}+2{x} -8\), можно сделать вывод, что \(\displaystyle y\) тоже должен быть равен\( \displaystyle 0\), либо \(\displaystyle y={{x}^{2}}+2{x} -8=0.\)

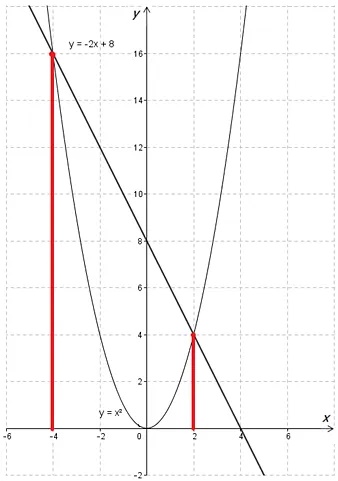
Способ 2 заключается в разбивке уравнения на несколько функций. Можно записать исходное уравнение \(\displaystyle {{x}^{2}}+2{x} -8=0\) по-другому, то есть:

\(\displaystyle {{x}^{2}}=8-2x\)

Преобразование является равносильным. Далее необходимо построить отдельно пару функций:

• \(\displaystyle {{y}_{1}}={{x}^{2}}\) — график представляет собой простую параболу, которую можно построить, не определяя вершину с помощью формул и подготовки таблицы для определения прочих точек;
• \(\displaystyle {{y}_{2}}=8-2x\) — график представляет сбой прямую, которую можно построить, подобрав значения \(\displaystyle x\) и \(\displaystyle y.\)

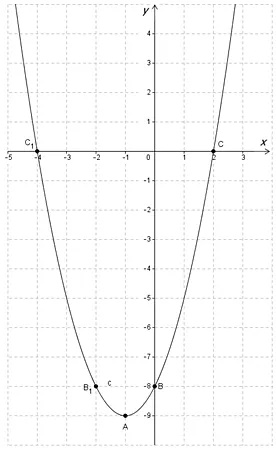
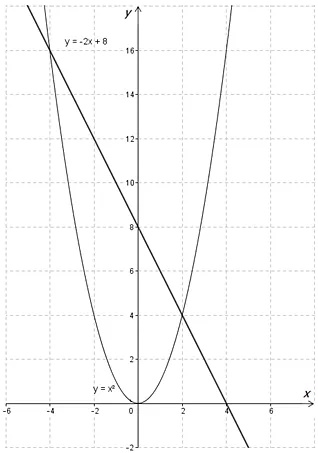
Графики:

Корнями уравнения являются координаты по \(\displaystyle x\), полученные, когда пересекаются графики: \(\displaystyle {{y}_{1}}={{x}^{2}}\) и \(\displaystyle {{y}_{2}}=8-2x\). Таким образом:

В таком случае уравнение будет иметь следующие решения:

\(\displaystyle {{x}_{1}}=2\)

\(\displaystyle {{x}_{2}}=-4\)

В качестве другого примера можно решить следующее уравнение:

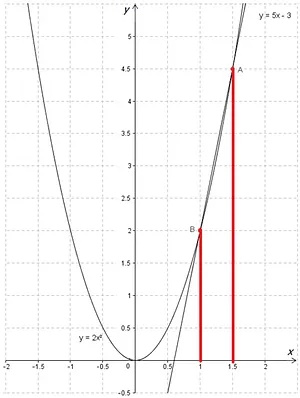
\(\displaystyle 2{{x}^{2}}-5x+3=0\)

Получатся графики:
\(\displaystyle {{y}_{1}}=2{{x}^{2}}\)

\(\displaystyle {{y}_{2}}=5{x} -3\)

Таким образом, корнями уравнения являются:

\(\displaystyle {{x}_{1}}=1\)
\(\displaystyle {{x}_{2}}=1,5\)

Графическое решение смешанных уравнений

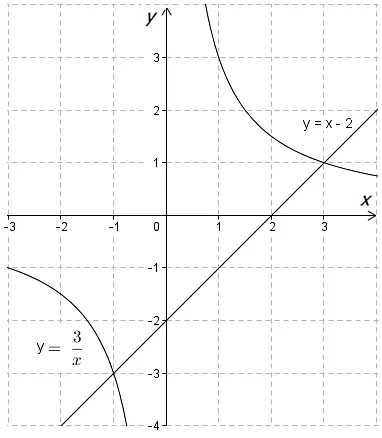
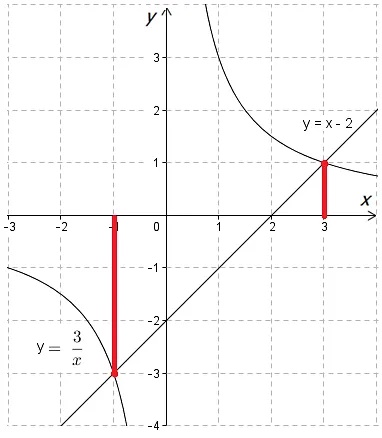
Разобрать данный способ можно на примере решения следующего уравнения:

\(\displaystyle \frac{3}{x}-x+2=0\)

Нужно построить пару графиков:

\(\displaystyle {{y}_{1}}=\frac{3}{x}\) — график представляет собой гиперболу.

\(\displaystyle {{y}_{2}}={x} -2\) — график является прямой, которую можно построить, подобрав значения \(\displaystyle x\) и \(\displaystyle x.\)
В результате получим следующие графики:

Таким образом, корнями уравнения являются:

\(\displaystyle {{x}_{1}}=-1\)

\(\displaystyle {{x}_{2}}=3\)

Ответ можно подтвердить, таким образом:

При подстановке корней в уравнение получим:

При\( \displaystyle {{x}_{1}}=-1:\frac{3}{-1}-\left( -1 \right)+2=-3+1+2=0.\)

При \(\displaystyle {{x}_{2}}=3:\frac{3}{3}-3+2=1-3+2=0.\)

Второй пример заключается в решении следующего уравнения:

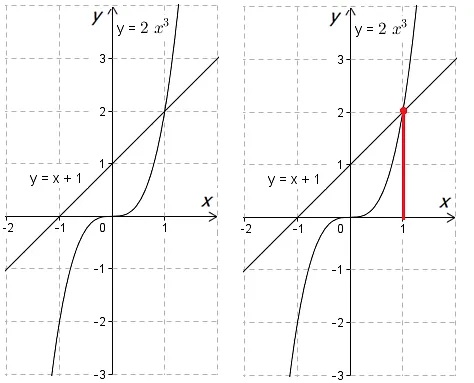
\(\displaystyle 2{{x}^{3}}-{x} -1=0\)

В данном случае целесообразно сначала перенести часть уравнения в правую сторону. Таким образом, в обеих частях останутся функции, которые просто построить:

\(\displaystyle 2{{x}^{3}}=x+1\), соответственно:

\(\displaystyle {{y}_{1}}=2{{x}^{3}}\) — кубическая парабола.

\(\displaystyle {{y}_{2}}=x+1\) — обыкновенная прямая.

В результате получим корень уравнения:

\(\displaystyle {{x}_{1}}=1\)

Дробные уравнения с одной переменной

При решении уравнений с дробями, которые содержат одну переменную, можно руководствоваться стандартным алгоритмом. Последовательность действий такова:

• определение области допустимых значений;
• поиск общего знаменателя;
• умножение каждого компонента уравнения на общий знаменатель для последующего сокращения полученных дробей и исключения знаменателей;
• раскрытие скобок, что моет сопровождаться приведением подобных слагаемых;
• решение полученного уравнения;
• сравнение полученных корней с областью дополнительных значений;
• запись ответа, который был предварительно проверен.

Метод пропорции

Данный способ подразумевает приведение дроби к общему знаменателю.

Рассмотреть эту закономерность удобно на практическом примере. Требуется решить линейное уравнение, в котором есть дроби:

Левая часть уравнения содержит одну дробь. Ее можно не преобразовывать. Правая часть уравнения включает сумму, которую следует упростить до получения одной дроби.

Решение:

В итоге левая и правая части уравнения содержат одну дробь. Далее необходимо воспользоваться методом пропорции и перемножить крест-накрест числители и знаменатели:

Метод избавления от дробей

Рассмотрим уравнение из предыдущего примера, но с другим решением:

Уравнение содержит пару дробей, которые необходимо исключить. Порядок действий следующий:

• подбор числа, которое можно разделить на каждый знаменатель без остатка;
• умножение данного числа на каждый компонент уравнения.

В рассматриваемом примере нужно найти наименьшее число, которое без остатка можно разделить на 5 и 9. Число 45 подходящее. Следует умножить на 45 каждый член уравнения и исключить знаменатели.

Линейные уравнения с одной переменной со скобками

Решение линейных уравнений данным способом заключается в следующих действиях:

• раскрытие скобок;
• перенесение х в левую часть уравнения, а чисел — в правую;
• приведение подобных слагаемых.

Полученное уравнение будет иметь вид: ax=b, которое является корнем рассматриваемого линейного уравнения: x=ba.

Данный метод можно рассмотреть на примере уравнения, которое необходимо решить:

2x+1=2(x−3)+8

Данное уравнение является линейным, так как переменная стоит в первой степени. В первую очередь уравнение необходимо привести к виду: ax=b. Для этого следует раскрыть скобки:

2x+1=4x−6+8

В левую часть нужно перенести все слагаемые, содержащие х, а в правую — числа:

2x−4x=2−1

−2x=1

Далее следует поделить обе части уравнения на число (-2):

−2x−2=1−2=−12=−0,5

Ответ: х=-0,5

В качестве примера можно решить еще несколько задач распространенного типа. Дано уравнение, корни которого нужно найти:

2x−4=2(x−2)

Данное уравнение является линейным. Следует избавиться от скобок, перенести х в левую часть, а числа — в правую:

2x−4=2x−4

2x−2x=−4+4

0=0

В результате преобразований было получено справедливое равенство. Можно сделать вывод, что от значения х тождество не зависит. Таким образом, х является любым числом.

Ответ: x∈(−∞; +∞)

Во втором примере необходимо решить уравнение:

2x−4=2(x−8)

Данное уравнение является линейным. Требуется раскрыть скобки, перенести х в левую часть, а числа — в правую:

2x−4=2x−16

2x−2x=−16+4

0=−12

В итоге х будет сокращен, и получилось неверное равенство. Таким образом. При любом х равенство будет неверным. В таком случае отсутствуют значения х, при которых получилось бы справедливое тождество.

Ответ: x∈∅

Примеры решений

Задача 1

Нужно найти корни уравнения:

0,9x-0,6(x-3)=2(0,2x-1,3)

Решение:

В первую очередь следует раскрыть скобки и привести подобные:

0,9x-0,6x+1,8=0,4x-2,6

0,3x+1,8=0,4x-2,6

Далее необходимо перенести слагаемые, в которых присутствует неизвестная, в одну часть, а слагаемые без неизвестной — в другую:

1,8+2,6=0,4x-0,3x

4,4=0,1x

После того, как две части уравнения будут умножены на 10, получим:

x=44

Ответ: x=44

Задача 2

Необходимо решить уравнение:

-36(6x+1)=9(4-2x)

Решение:

После раскрытия скобок в обеих частях равенства получим:

-216x-36=36-18x

Далее можно перенести переменные в правую часть, а остальные слагаемые — в левую:

-36-36=-18x+216x

После приведения подобных получим:

-72=198x

Затем стоит разделить правую и левую часть уравнения на 198:

\(x=\frac{-72}{198}\)

Сократив дробь на 18. получим:

\(x=-\frac{4}{11}\)

Ответ: \(x=-\frac{4}{11}\)

Задача 3

Нужно определить наибольший из корней уравнения:

(1,8-0,3y)(2y+9)=0

Решение:

В данном случае целесообразно применить свойство произведения. Произведение равно нулю, тогда и только тогда, когда один из множителей равен нулю. Таким образом, одно из выражений в скобках должно обладать нулевым значением.

В первом случае:

\(1,8-0,3y=0\Rightarrow 1,8=0,3y\)

Следует перенести слагаемые и умножить обе части уравнения на 10, а затем, поделить на 3:

\(\frac{1,8\cdot 10}{3}=\frac{0,3y\cdot 10}{3}\)

\(\frac{18}{3}=\frac{3y}{3}\)

y=6

Второй случай:

2y+9=0

2y=-9

Поделив обе части уравнения на 2, получим:

\(y=\frac{-9}{2}\)

y=-4,5

Таким образом, уравнением имеет пару корней, обращающих его в 0. Если выбрать наибольший из них, то:

y=6

Ответ: y=6

Задача 4

Дано уравнение, корень которого необходимо найти:

\(\frac{3m+5}{4}=\frac{5m+1}{3}\)

Решение:

В первую очередь следует умножить обе части уравнения на общий знаменатель 12, то есть на 4 и 3, чтобы привести его к виду: x=…

\(\frac{3m+5}{4}\cdot \frac{4\cdot 3}{1}=\frac{5m+1}{3}\cdot \frac{4\cdot 3}{1}\)

Сокращая слева на 4, а справа на 3 получим:

\((3m+5)\cdot 3=(5m+1)\cdot 4\)

Далее нужно раскрыть скобки:

\(3m\cdot 3+5\cdot 3=5m\cdot 4+1\cdot 4\)

\(9m+15=20m+4\)

В рассматриваемом примере целесообразно перенести 9m в правую часть равенства, чтобы не избавляться от минуса. После переноса слагаемых необходимо привести подобные и записать ответ:

15-4=20m-9m

11=11m

m=1

Ответ: m=1

Задача 5

Необходимо определить такое значение а, при котором корень уравнения будет равен -9:

3ax=12-x

Решение:

Путем подстановки -9 на место х можно получить а, при котором такая ситуация имеет место:

\(3a\cdot (-9)=12-(-9)\)

Далее следует обратить внимание на правую часть уравнения и воспользоваться свойством: в том случае, когда перед скобками стоит знак минус, при их раскрытии все знаки, которые стоят в скобках, меняются на противоположные. Получим:

-27a=12+9

-27a=21

Затем можно поделить правую и левую части уравнения на (-27):

\(a=\frac{21}{-27}\)

После сокращения правой части равенства на 3 получим ответ:

\(a=-\frac{7}{9}\)

Ответ: \(a=-\frac{7}{9}\)