Как найти медиану треугольника

Что такое медиана треугольника

Треугольник представляет собой геометрический объект на плоскости, состоящий из трех точек, расположенных на разных прямых, которые соединены между собой с помощью отрезков. В данной фигуре допустимо построить определенные элементы, в том числе, медиану. Определение и свойство такого компонента позволяют решать множество задач в планиметрии. Начать изучение понятия целесообразно с расшифровки термина.

При наличии прочих компонентов, характерных для треугольной геометрической формы, важно отличать от них медиану. Исследуемый тип отрезка обладает некоторыми особенностями построения. В процессе изображения линии целесообразно руководствоваться следующим алгоритмом действий:

• определить точку, которая делит сторону треугольной фигуры на пару равных отрезков;
• соединить точку, найденную на первом шаге, с противоположной вершиной;
• полученный отрезок обозначить за медиану.

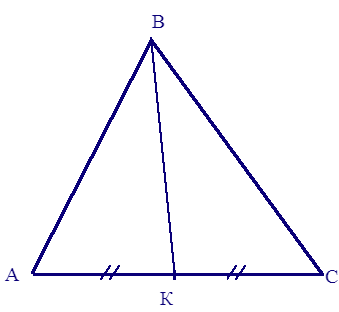
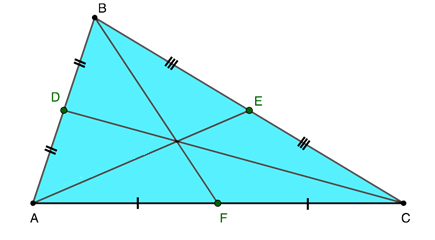
Наглядно ознакомиться с графической схемой получения медианы в треугольном геометрическом объекте произвольного вида можно на рисунке ниже:

 

Заметим, что на изображении, представленном выше, треугольник построен из трех отрезков, играющих роль его сторон. Руководствуясь определением медианы, допустимо утверждать наличие возможности для построения трех таких линий для одного треугольного объекта. При изучении этого действия пригодится понятие медианного основания.

Все три возможных варианта медианных линий в треугольнике обладают единой точкой пересечения. При сравнении медианы с прочими элементами следует отметить значимое соотношение величин. В процессе построения медианы, биссектрисы и высоты из одинаковой вершины треугольной фигуры максимальный размер характерен для первого типа отрезка.

Свойства

Упростить решение большинства задач на проведение или вычисление размера медианы в треугольнике позволяет ряд полезных свойств. Закономерности прикладного назначения выявляют связь между разными компонентами треугольной геометрической фигуры. По этой причине, руководствуясь доступной информацией, можно быстро найти величину медианы, либо других искомых элементов.

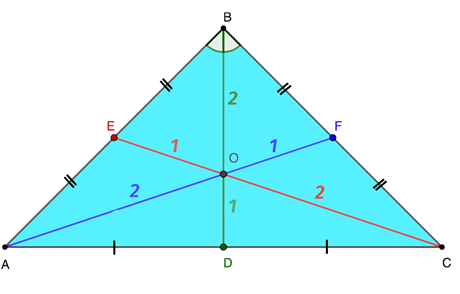
Главное свойство состоит в определении количества медиан в произвольном треугольнике. Исходя из того, что подобный объект обладает тремя вершинами и аналогичным числом сторон, представляется возможным построить три медианы соответственно. Образованные в результате отрезки обладают единственной точкой пересечения. Такую отметку можно обозначить за О на рисунке и назвать центроидом или центром тяжести треугольной фигуры.

 

Источник: microexcel.ru

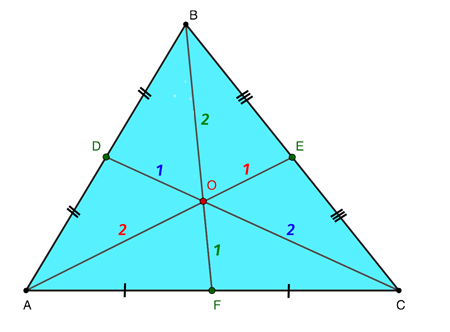
Рассматриваемая точка выделяет в каждой из медианных линий два отрезка, которые соотнесены друг с другом, как 2 к 1, если вести счет, начиная с вершины. Таким образом, справедливо записать следующие верные равенства:

AO = 2OE

BO = 2OF

CO = 2OD

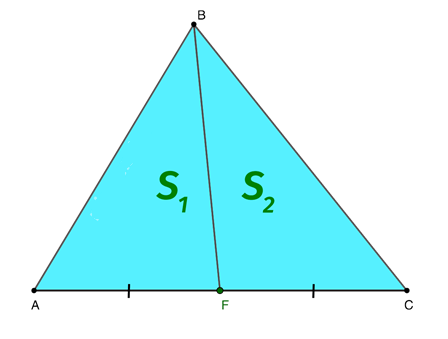
С помощью медианы, которая проведена из какой-либо вершины в произвольном треугольнике, всегда получают пару новых треугольных объектов, обладающих идентичными площадями. Озвученные фигуры называют равновеликими. На изображении ниже представлены такие треугольники в качестве примера. S1 и S2 обозначают площади этих объектов и равны между собой.

 

Источник: microexcel.ru

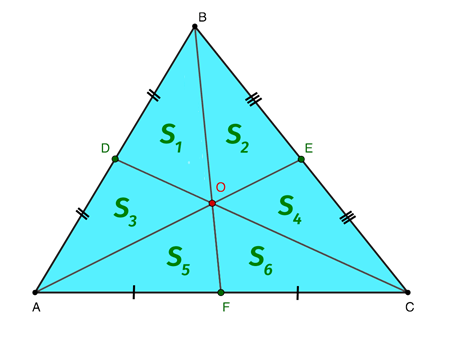
Следующее свойство заключается в делении тремя медианами треугольной геометрической фигуры, в которой они построены, на три пары треугольников, являющихся равновеликими, то есть имеющих идентичные размеры площадей. Если обозначить площадь за S, то сформулировать озвученную закономерность можно с помощью математического соотношения:

S1 = S2 = S3 = S4 = S5 = S6

 

Источник: microexcel.ru

Другим полезным свойством служит соответствие медианы с минимальным размером наиболее крупной стороне треугольного объекта. Справедливо и обратное высказывание. Представим, что АС является стороной в фигуре, обладающей максимальной среди всех подобных элементов длиной. Тогда медиана BF меньше остальных медианных отрезков. Исходя из того, что АВ меньшая сторона, справедливо обозначить наибольшую медиану за CD. Описанные закономерности можно перенести на рисунок:

 

Источник: microexcel.ru

Как найти: формулы

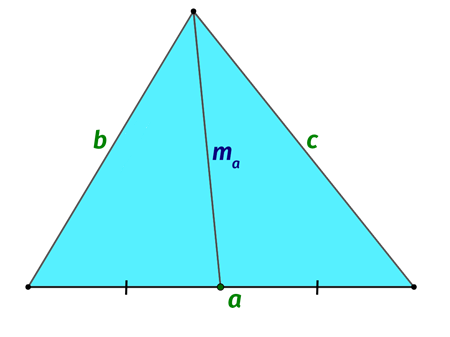
Во многих практических заданиях по планиметрии применяют формулы и закономерности. Предусмотрено универсальное алгебраическое выражение, с помощью которого несложно вычислить размер медианы в произвольном треугольнике. Представим, что в рассматриваемой фигуре стороны составляют а, b и с. Изобразим графически сформулированные условия:

 

Источник: microexcel.ru

Предположим, что длина медианного отрезка является \(m_{a}\). Тогда для выполнения расчета этого параметра следует применить подходящую формулу:

\(m_{a} = \sqrt{\frac{2b^{2}+2c^{2}-a^{2}}{4}}\)

В прямоугольном треугольнике

Прямоугольным треугольник называют по причине наличия одного угла, градусная мера которого составляет 90°. Остальные углы в такой фигуре острые. Как и в прочих типах треугольных объектов, в прямоугольном треугольнике можно провести медианы. Рассмотрим случай, когда в подобной геометрической форме с прямым углом ВАС построили медиану AD на гипотенузу ВС. Полученный отрезок составляет 50% от длины гипотенузы, на которую он опирается, то есть:

BC = 2AD

AD = BD = DC

Соответствует действительности и обратное утверждение. При наличии в треугольнике медианы, составляющей вторую часть от стороны, которую она пересекает, данная сторона является гипотенузой. При соблюдении озвученных условий исследуемый объект идентифицируют как прямоугольную треугольную фигуру.

В случае треугольника с прямым углом величину медианы допустимо вычислять по специальному алгебраическому выражению, которое сформулировано с помощью теоремы Пифагора и адаптировано под предыдущую закономерность рассмотренную выше:

\(AD = \frac{\sqrt{AB^{2}+AC^{2}}}{2}\)

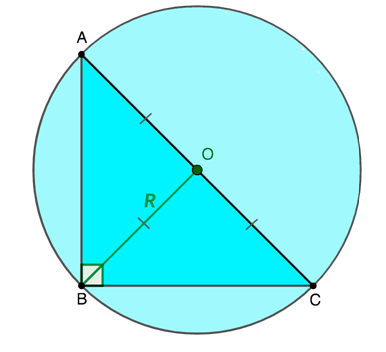
Другой часто применяемый формат расчета длины медианы предполагает оперирование исходными значениями величины гипотенузы, на которую она опирается, и радиуса окружности, описанной около прямоугольного треугольника. Тогда формула для вычислений приобретает следующий вид:

OB = R

 

Источник: microexcel.ru

В равностороннем

В равностороннем треугольнике все стороны обладают одинаковыми длинами. В связи с этой особенностью геометрической фигуры любая поведенная медиана в одно и то же время играет роль высоты, серединного перпендикуляра и биссектрисы угла, из которого построен отрезок.

 

Источник: microexcel.ru

В равносторонней треугольной фигуре медианы, проведенные из разных вершин, обладают одинаковыми размерами. Обозначим такие отрезки и составим справедливое равенство:

AF = BD = CE

 

Источник: microexcel.ru

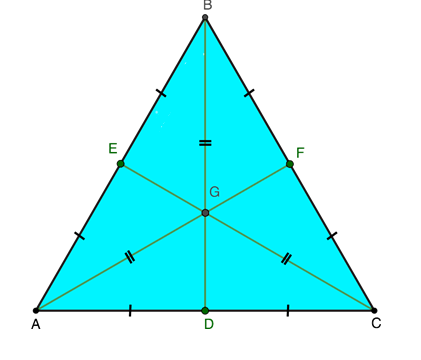
Если в треугольнике с равными сторонами медианы обладают одной точкой пересечения, то такая отметка делит их на отрезки, один из которых в два раза длиннее другого. Это свойство применимо к решению многих задач на вычисление элементов в равносторонней треугольной фигуре.

 

Источник: microexcel.ru

AG = 2GF;

BG = 2GD;

CG = 2GE.

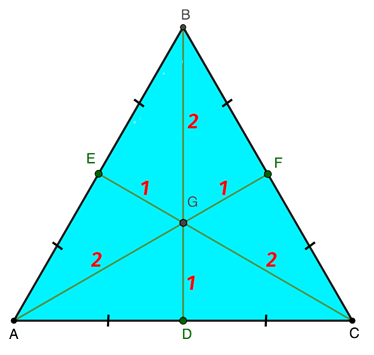
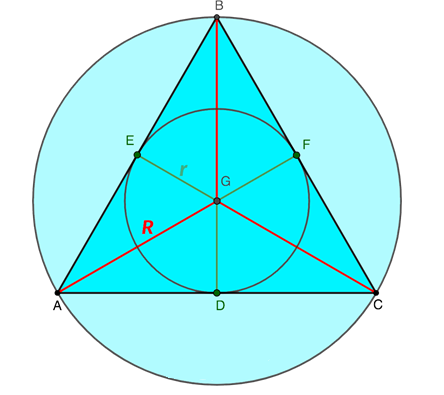
Если провести из любой вершины равностороннего треугольника медиану, то полученный отрезок поделит фигуру на пару одинаковых треугольных объекта с прямыми углами и равными площадями. При построении сразу трех медиан в аналогичной геометрической форме образуется шесть равновеликих прямоугольных треугольника. Точка, в которой медианы пересекают друг друга, служит центром для описанной и вписанной окружности.

 

Источник: microexcel.ru

Заметим, что из предыдущего свойства медианы в равностороннем треугольнике вытекает следствие, которое можно представить в виде математического соотношения:

R = 2r

С целью вычисления размера медианы в треугольной фигуре с равными сторонами а применяют следующую формулу:

\(m_{a}=\frac{\sqrt{3}a}{2}\)

В равнобедренном

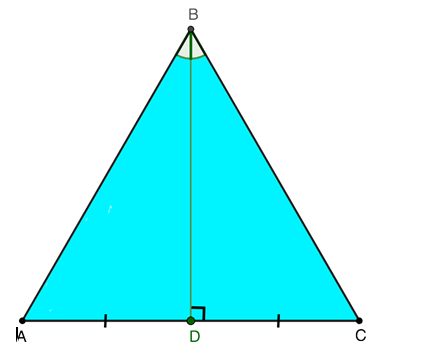
Равнобедренным считают такой треугольник, у которого пара равных сторон, а третья сторона является основанием. Изобразим графическим способом озвученную формулировку. Обозначим за боковые элементы отрезки АВ и ВС, основанием служит сторона АС.

 

Источник: microexcel.ru

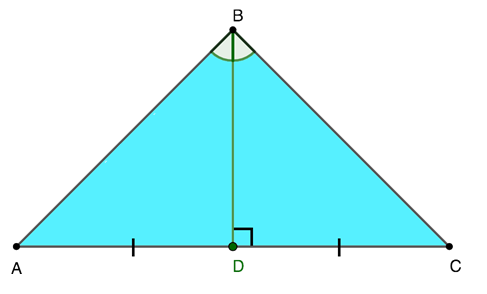
В представленной выше равнобедренной треугольной фигуре медиана, проведенная к основанию, выполняет сразу несколько функций:

• высота к основанию треугольника;
• биссектриса угла, из вершины которого построен медианный отрезок.

Как и в предыдущих вариантах начертания треугольников, в равнобедренном геометрическом объекте с тремя углами при пересечении трех медиан образуются отрезки, которые соотносятся между собой в соответствии с пропорцией 2:1. Утверждение можно наглядно представить на изображении:

 

Источник: microexcel.ru

AO = 2OF

BO = 2OD

CO = 2OE

С помощью медианы из равнобедренного треугольника получают пару одинаковых по площади треугольных фигур. При построении сразу трех медиан количество равновеликих треугольных объектов возрастает до шести. С целью вычисления величины медианы, которая проведена к основанию а равнобедренного треугольника, применяют формулу:

\(m_{a}=\frac{1}{2}\sqrt{4b^{2}-а^{2}}\)

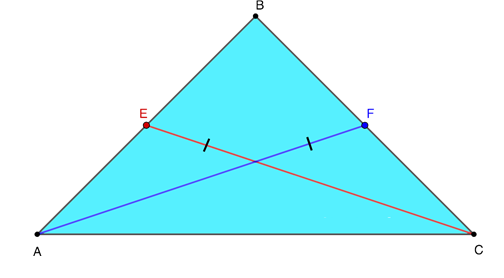
В некоторых задачах по геометрии встречаются медианы, построенные не к основанию, а к другим сторонам треугольной равнобедренной фигуры. В таком случае отрезки равны по длине. Применительно к рисунку ниже допустимо записать следующие соотношения:

AF = CE

AE = EB = BF = FC

 

Источник: microexcel.ru

Примеры решения задач

Решение

В данном случае целесообразно применить в процессе решения свойство медиан в треугольнике. Зная, что 3 медианных отрезка делят треугольный объект на 6 равновеликих фигур, допустимо составить следующее соотношение для вычисления общей площади:

\(S = 5 \cdot 6 = 30 (см^{2})\)

Ответ: S = \(30 см^{2}\).

Решение

Из курса теории понятно, что при известных величинах сторон треугольника несложно вычислить размер проведенной в нем медианы. Воспользуемся общей формулой для расчета длины этого отрезка. Путем подстановки численных значений из условий задания рассчитаем искомую величину и запишем ответ:

\(m_{а} = \sqrt{\frac{2b^{2}+2c^{2}-a^{2}}{4}}\)

\(m_{6} = \sqrt{\frac{2\cdot 8^{2}+2\cdot 10^{2}-6^{2}}{4}} \approx 8,54 (см)\)

Ответ: \(m_{6} = 8,54 см.\)

Решение

Заметим, что речь в задании идет о прямоугольном треугольнике. Согласно закономерности, описанной в разделе с теорией, гипотенуза вдвое больше по сравнению с медианой. Вычислим ее значение с помощью простого уравнения:

\(10\cdot 2 = 20 (см)\)

Далее полезно применить теорему Пифагора с целью расчета размера второго катета. Введем для удобства выполнения вычислений обозначение данного отрезка b. Тогда катет, величина которого известна, примем за а. Гипотенузу обозначим, как с. Используя сокращенные идентификаторы элементов треугольника, составим математическое соотношение для определения катета b:

\(b^{2} = с^{2} - а^{2} = 20^{2} - 12^{2} = 256\)

b = 16 (см)

Когда длины всех сторон прямоугольного треугольника известны, допустимо приступить к расчету искомого периметра. С этой целью выполним сложение величин сторон и сформулируем ответ:

Р = 12 + 16 + 20 = 48 (см)

Ответ: Р = 48 см.

Решение

Воспользуемся формулой вычисления длины медианы для равносторонней треугольной фигуры. Подставим численные значения из условия задачи и запишем полученный ответ:

\(m = \frac{\sqrt{3}\cdot 6}{2}\approx 5,2 (см)\)

Ответ: m = 5,2 см.

Решение

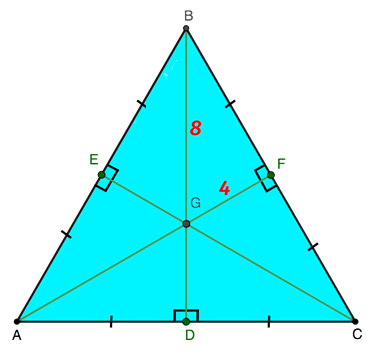
С целью исключить ошибки в процессе решения задания следует выполнить рисунок геометрической фигуры, о которой идет речь в условии. Построим графическое изображение равностороннего треугольника и его элементов:

 

Источник: microexcel.ru

На рисунке хорошо заметны 6 прямоугольных треугольников, образованных по итогам пересечения 3 медиан. Наибольшей стороной является BG с длиной 8 см, которая играет роль гипотенузы в треугольной фигуре BFG. При этом вдвое меньше катет FG, что вытекает из ранее изученного свойства. Таким образом, FG составляет 4 см.

На следующем шаге решения целесообразно обратиться к теореме Пифагора для вычисления величины второго катета BF. Запишем подходящую формулу и подставим числовые значения:

\(BF^{2} = BG^{2} – FG^{2} = 8^{2} – 4^{2} = 48 (см^{2})\)

\(BF \approx 6,93 (см)\)

Исходя из того факта, что медиана делит на две равные части сторону треугольной равносторонней фигуры, сформулируем справедливое соотношение:

\(BF = \frac{BC}{2}\)

Выполним необходимые вычисления и запишем ответ:

\(ВС = BF\cdot 2 \approx 13,86 (см)\)

Ответ: \(ВС \approx 13,86 см\).

Решение

Вспомним из теоретического материала формулу для расчета длины медианы с учетом того, что в условии задания речь идет о равнобедренной треугольной фигуре. Запишем алгебраическое соотношение с подстановкой известных величин и найдем искомый ответ:

\(m = \frac{1}{2}\sqrt{4\cdot 12^{2}- 7^{2}}\approx 11,48 (см)\)

Ответ: m = 11,48 см.