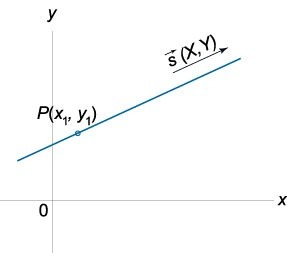Определение направляющего вектора прямой и как его найти

Направляющий вектор прямой

В геометрии можно встретить множество задач на изучение прямой в пространстве и ее свойств. В трехмерном пространстве рассматривают не только прямую, но и плоскость. Данные объекты достаточно просто задать, используя направляющие векторы.

Согласно определению, можно сделать вывод о существовании бесконечного множества направляющих векторов прямой, которая задана. Кроме того, какой-либо направляющий вектор прямой расположен либо на рассматриваемой прямой, либо на прямой, которая ей параллельна. Таким образом, все направляющие векторы заданной прямой коллинеарны.

Отсюда следует, что при \(\vec{a}\) направляющем векторе прямой а, каждое из направлений \(t*\vec{a}\), где t определяется некоторым ненулевым действительным значением, также представляет собой направляющий вектор прямой а, что следует из условия коллинеарности векторов.

Исходя из термина направляющего вектора прямой, следует, что множества направляющих векторов параллельных прямых совпадают. По-другому, данное утверждение можно сформулировать так: в том случае, когда прямые а и а1 параллельны, вектор \(\vec{a}\) является направляющим вектором прямой а, при этом вектор \(\vec{a}\) также является направляющим вектором прямой а1.

Кроме того, из определений направляющего вектора прямой и нормального вектора прямой следует, что каждый нормальный вектор прямой а является перпендикуляром каждому направляющему вектору прямой а.

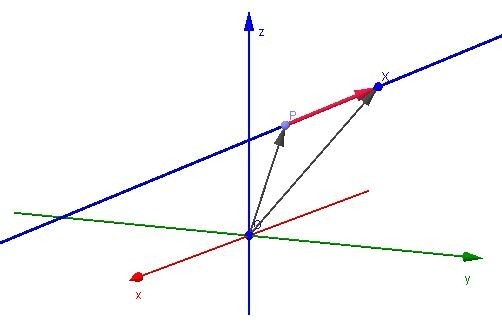
На примере можно рассмотреть направляющий вектор прямой. Предположим, что в трехмерном пространстве имеется прямоугольная система координат Охуz. Координатные векторы \( \vec{i}, \ \vec{j}, \ \vec{k}\) представляют собой направляющие векторы координатных прямых Ох, Оу, Оz соответственно.

Можно рассмотреть другой пример, где задан вектор \(\vec{v}\). Его координаты известны (а; b; с). Так как имеется три координаты, то можно заключить, что вектор задан в пространстве. Для того чтобы изобразить рассматриваемый вектор в прямоугольной системе координат, на каждой из трех осей требуется отложить прямую, ограниченную двумя точками, то есть отрезок с длиной, равной соответствующей координате сектора.

Три перпендикуляра, которые восстановлены к плоскостям xy, yz и xz, будут пересекаться в точке, являющейся концом вектора. Начало вектора совпадает с точкой (0; 0; 0). Однако рассматриваемое положение вектора не единственное. Таким же образом можно задать вектор \(\vec{v}\) с началом в произвольной точке пространства.

Отсюда следует вывод о невозможности задания конкретной прямой с помощью вектора. С его помощью можно определить комплекс из бесконечного числа параллельных прямых.

Далее можно отметить в пространстве какую-либо точку P(x0; y0; z0). Следует определить условие, что через данную точку должна проходить прямая. Таким образом, заданная точка будет располагаться на векторе \(\vec{v}\). Исходя из этого, можно сделать вывод, что прямая, заданная с помощью \(Р\) и \(\vec{v}\), является единственной. Уравнение данной прямой будет иметь вид:

\(Q=P+\lambda*\vec{v}\)

 где Q является любой точкой, которая принадлежит рассматриваемой прямой.

Данная точка получается путем подбора соответствующего параметра \(\lambda\). Представленная запись уравнения является векторной, а \(\vec{v}\) представляет собой направляющий вектор прямой. В том случае, когда этот вектор пересекает Р и изменяется в длине по параметру \(\lambda\), получается какая-либо точка Q прямой. Координатная форма уравнения:

\((x;y;z) = (x_{0};y_{0};z_{0})+\lambda*(a;b;c)\)

Параметрический вид уравнения:

\(x=x_{0}+\lambda*a;\)

\(y = y_{0}+\lambda *b;\)

\(z = z_{0} + \lambda *c\)

Когда нужно знать направляющий вектор

Данные знания пригодятся при решении задач на определение параллельности и перпендикулярности прямых. Кроме того, направляющий вектор используют для расчета расстояния между прямыми, а также точкой и прямой, описания поведения прямой относительно плоскости.

Одна прямая будет параллельна второй прямой в том случае, когда их направляющие вектора параллельны. Аналогично, перпендикулярность прямых доказывают через перпендикулярность их векторов. Подобные задачи предполагают необходимость определения скалярного произведения рассматриваемых векторов для получения ответа.

Когда требуется вычислить расстояние между прямыми и точками, целесообразно использовать формулу с направляющим вектором:

\(d=\frac{\left|\left[\vec{P_{1}P_{2} }*\vec{v}\right]\right|} {\left| \vec{v}\right|}\)

В данном случае \(\vec{P_{1}P_{2} }\) является построенным на точках P1 и P2 направленным отрезком. Точка P2 произвольно расположена на прямой с вектором \(*\vec{v}\), а до точки Р1 требуется определить расстояние. Данная точка является самостоятельной, либо расположена на другой прямой или находится в другой плоскости.

Следует заметить, что рассчитывать расстояние целесообразно только между параллельными или скрещивающимися прямыми. В том случае, когда прямые пересекаются, d обладает нулевым значением. Записанная формула для d справедлива и для расчета дистанции между плоскостью и параллельной ей прямой. Но при этом P1 расположена в рассматриваемой плоскости.

Задача на составление векторного уравнения

Представим, что имеется следующее уравнение прямой:

\(y = 3 × x – 4\)

Необходимо записать векторное уравнение данной прямой.

Допустимо переписать выражение в виде:

\((x; y) = (x; 3 × x - 4)\)

При раскрытии данного уравнения будет получено выражение из условия.

Далее можно разделить правую часть уравнения на вектора таким образом, чтобы лишь один из них включал неизвестные:

\((x; y) = (x; 3 × x) + (0; -4)\)

Затем следует вынести х за скобки, обозначить его \(\lambda\) и поменять вектора правой части местами:

\((x; y) = (0; -4) + \lambda * (1; 3)\)

Таким образом, получена векторная форма уравнения прямой из условия. Координаты ее направляющего вектора равны (1; 3).

Задача на определение взаимного расположения прямых

Представим, что в пространстве задана пара прямых:

\((x; y; z) = (1; 0; -2) + \lambda * (-1; 3; 1);\)

\((x; y; z) = (3; 2; 2) + \lambda * (1; 2; 0)\)

Необходимо определить, какие эти прямые: параллельные, скрещивающиеся или пересекающиеся. При этом ненулевые вектора (-1; 3; 1) и (1; 2; 0) являются направляющими для заданных прямых. Можно выразить в параметрической форме рассматриваемые уравнения и подставить координаты первого во второе:

\(x = 1 - \lambda;\)

\(y = 3 * \lambda;\)

\(z = -2 + \lambda;\)

\(x = 3 + \gamma = 1 - \lambda => \gamma = -2 - \lambda;\)

\(y = 2 + 2 * \gamma = 3 * \lambda => \gamma = 3 / 2 * \lambda - 1;\)

\(z = 2 = -2 + \lambda => \lambda = 4\)

При подстановке определенного параметра \(\lambda \)в два уравнения выше, получится:

\(\gamma = -2 - \lambda = -6;\)

\(\gamma = 3 / 2 *\lambda - 1 = 5\)

Для параметра \(\gamma\) не предусмотрено наличие сразу двух значений. Таким образом, прямые не обладают ни одной общей точкой, то есть являются скрещивающимися. Параллельность данных прямых исключается, так как ненулевые векторы не параллельны друг другу, то есть для их параллельности должно существовать число, которое бы путем умножения на один вектор приводило к координатам второго.

Математическое описание плоскости

Задать плоскость в пространстве можно путем приведения уравнения общего вида:

\(A * x + B * y + C * z + D = 0\)

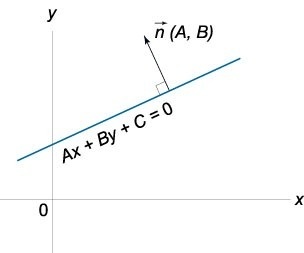
В данном случае латинскими большими буквами обозначают конкретные числа. Первая тройка таких чисел определяет координаты нормального вектора плоскости. В том случае, когда он обозначен \(\vec{n}\), можно записать: \(\vec{n} = (A; B; C)\). Рассматриваемый вектор перпендикулярен к плоскости, поэтому его называют направляющим.

Его знание, а также известные координаты любой точки, находящейся на плоскости, однозначно задают последнюю. Если точка P (x1; y1; z1) плоскости принадлежит, то свободный член D рассчитывается следующим образом:

\(D = -1 * (A * x1 + B * y1 + C * z1)\)

Уравнение прямой по направляющему вектору

Любой ненулевой вектор \(\vec{a} (а1; \ а2)\) с компонентами, соответствующими условию А а1 + В а2 = 0, представляет собой направляющий вектор прямой.

Ах + Ву + С = 0

В качестве примера можно вывести уравнение прямой, которая проходит через точку А (1, 2) с направляющим вектором \(\vec{a} \) (1, -1). Для этого требуется записать уравнение в виде:

Ax + By + C = 0

Согласно определению, коэффициенты должны соответствовать следующим условиям:

1 * A + (-1) * B = 0, то есть А = В

В таком случае:

Ax + Ay + C = 0, или x + y + C / A = 0

Если х = 1, у = 2 получаем:

С/ A = -3

Таким образом:

х + у - 3 = 0

Общее уравнение прямой в декартовой системе координат имеет вид:

Ax + By + C = 0

где x, y – являются координатами точек прямой, A, B, C – определяются, как действительные числа при условии \({A^2} + {B^2} \ne 0\).

В том случае, когда прямая задана общим уравнением:

Ax + By + C = 0

В таком случае вектор:

\(\mathbf{n}\left( {A,B} \right)\)

Его координаты соответствуют коэффициентам A, B. Данный вектор представляет собой вектор нормали к данной прямой.

Уравнение прямой по точке и направляющему вектору представляет собой каноническое уравнение прямой и имеет вид:

\(\large\frac{{x - {x_1}}}{X}\normalsize = \large\frac{{y - {y_1}}}{Y}\normalsize\)

где вектор \(\mathbf{s}\left( {X,Y} \right)\) направлен вдоль прямой, а точка \(P\left( {{x_1},{y_1}} \right)\) расположена на этой прямой.

Координаты направляющего вектора из общего уравнения

При рассмотрении данной темы стоит привязать рассматриваемую прямую и ее направляющие векторы к прямоугольной системе координат. Алгоритм действий:

• рассмотреть прямую и ее направляющие векторы в прямоугольной декартовой системе координат Oxy на плоскости;
• рассмотреть прямую и ее направляющие векторы в прямоугольной системе координат Oxyz, принадлежащей трехмерному пространству.

Прямая линия в прямоугольной системе координат Oxy определяется некоторым уравнением прямой на плоскости. При этом направляющие вектора прямой в системе координат Oxy соответствуют координатам направляющих векторов.

Определить координаты направляющего вектора прямой при известном уравнении рассматриваемой прямой можно в том случае, когда прямая линия задана каноническим уравнением или параметрическими уравнениями.

Каноническое уравнение прямой на плоскости можно записать в виде:

\(\frac{x-x_{1}}{a_{x}}=\frac{y-y_{1}}{a_{y}}\)

Один из направляющих векторов этой прямой можно записать так:

\(\vec{a}(a_{x}; a_{y})\)

Отсюда следует вывод о том, что числа в знаменателях канонического уравнения прямой соответствуют координатам направляющего вектора рассматриваемой прямой.

\(\frac{x-1}{4}=\frac{y+1/2}{-3}\)

Необходимо рассчитать координаты любого направляющего вектора данной прямой.

Решение

Согласно каноническому уравнению прямой на плоскости, координаты какого-то из направляющих векторов рассматриваемой прямой соответствуют числам в знаменателях. Таким образом, искомый направляющий вектор обладает координатами (4; -3).

Ответ: (4; -3)

Подобным образом можно определить прямую с направляющим вектором \(\vec{a}(a_{x}; a_{y})\) с помощью параметрических уравнений прямой на плоскости:

\(x=x_{1}+a_{x}*\lambda\)

\(y=y_{1}+a_{y}*\lambda\)

Таким образом, коэффициенты при параметре в параметрических уравнениях прямой представляют собой соответствующие координаты направляющего вектора прямой.

\(x=-1\)

\(y=7-5*\lambda\)

При этом \(\lambda \in R\). Требуется определить координаты направляющих векторов заданной прямой.

Решение

В первую очередь следует преобразовать уравнение прямой:

\(x=-1+0*\lambda\)

\(y=7-5*\lambda\)

Коэффициенты с параметром \(\lambda\) соответствуют координатам направляющего вектора прямой:

\(\vec{a}(0; -5)\)

Данный вектор является одним из направляющих векторов исходной прямой. Так как направляющие вектора прямой коллинеарны, их можно записать в виде: \(t*\vec{a}\). В координатной форме запись будет иметь вид: \((0; -5*t)\). В данном случае t является любым действительным числом, которое не равно нулю.

Ответ: \((0; -5*t), t \in R, t\neq 0\)

Далее можно рассмотреть принцип поиска координат направляющего вектора прямой, заданной общим уравнением прямой вида: \(Ax + By + C = 0.\)

Ели А=0 в выражении Ах + Ву + С = 0, то уравнение будет записано в виде:

Ву + С = 0

Данное уравнение определяет прямую, которая параллельна оси абсцисс. Таким образом, направляющим вектором прямой \(Ву + С = 0\) является координатный вектор \(\vec{i}(1; 0).\)

Если В=0, то запись общего уравнения прямой будет следующая:

\(Ах + С = 0\)

Данная прямая параллельна оси ординат. В связи с этим, ее направляющим вектором будет координатный вектор \(\vec{j}(1; 0).\)

Решение

С помощью уравнения х-2=0 в прямоугольной системе координат Oxy можно задать прямую, которая будет параллельна оси Oy. Таким образом, роль ее направляющего вектора играет координатный вектор \(\vec{j}(0; 1).\)

Ответ: (0; 1)

В том случае, когда общее уравнение прямой имеет вид \(Ах + Ву + С = 0\) с коэффициентами А и В, не равными нулю, координаты направляющего вектора находят одним из следующих методов:

• приведение заданного уравнения в канонический вид, что позволит распознать координаты направляющего вектора;
• поиск координат пары не совпадающих точек на данной прямой, принятие их в качестве начала и конца направляющего вектора прямой и определение его координат;
• поиск координат любого вектора, который перпендикулярен к нормальному вектору \(\vec{n}(A; B)\) прямой \(Ах + Ву + С = 0.\)

\(3х + 2у – 10 = 0\)

Решение

В первую очередь необходимо привести общее уравнение прямой к каноническому виду. В данном случае в левой части выражения остается лишь слагаемое 3х, а остальные компоненты следует перенести в правую часть, меняя знак на противоположный:

\(3х + 2у – 10 = 0\)

\(3х = -2у + 10\)

Преобразованное равенство имеет вид:

\(3х = -2у + 10\)

\(3х = -2(у -5)\)

\(\frac{x}{-2}=\frac{y-5}{3}\)

Полученное уравнение позволяет сделать вывод о том, что координаты направляющего вектора равны (2;-3).

Ответ: (2;-3)

Координаты направляющего вектора из уравнения с угловым коэффициентом

Уравнение с угловым коэффициентом записывают в таком виде:

\(y=kx+b\)

Определить координаты направляющего вектора прямой, описанной данным уравнением, можно с помощью приведения рассматриваемого уравнения к общему виду. В процессе требуется перенести компоненты в левую часть:

\(y−kx–b=0\)

Далее можно прибегнуть к алгоритму, характерному для общего уравнения. Уравнение с угловым коэффициентом, преобразованное в каноническое, запишем следующим образом:

\(x1=y−bk\)

Таким образом, координаты направляющего вектора для данного случая равны:

\(\vec{S}=(1;k)\)

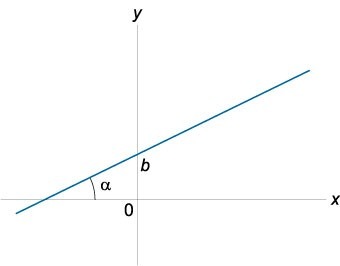
Уравнение прямой с угловым коэффициентом:

\(y = kx + b\)

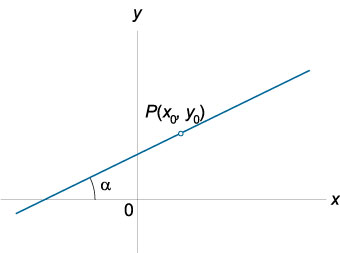
где \(k = \tan\alpha\) представляет собой угловой коэффициент прямой, число b определяется, как координата точки пересечения прямой с осью Oy.

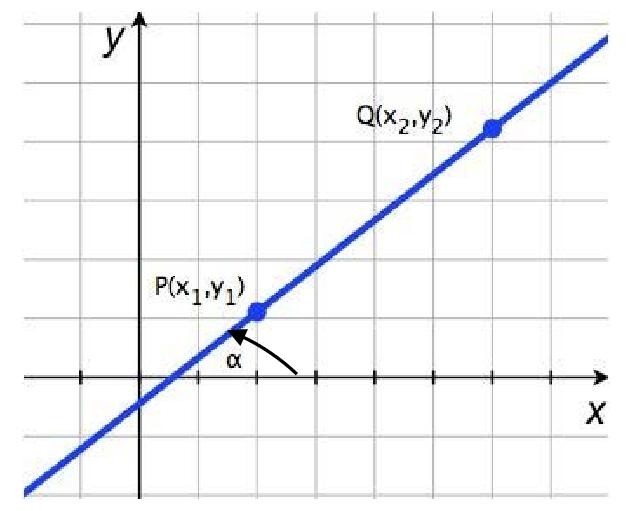
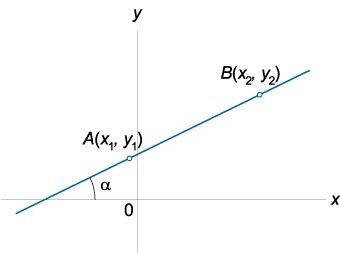
Угловой коэффициент прямой рассчитывают с помощью уравнения:

\(k = \tan \alpha = \large\frac{{{y_2} - {y_1}}}{{{x_2} - {x_1}}}\normalsize,\)

где \(A\left( {{x_1},{y_1}} \right), B\left( {{x_2},{y_2}} \right)\) – являются координатами двух точек, расположенных на прямой.

Уравнение прямой по точке и угловому коэффициенту имеет вид:

\(y = {y_0} + k\left( {x - {x_0}} \right),\)

где k – является угловым коэффициентом, а точка \(P\left( {{x_0},{y_0}} \right) \) расположена на рассматриваемой прямой.