Решение неопределенных интегралов

Что такое неопределенный интеграл

Существует множество математических направлений, часть из которых вызывают значительные трудности в процессе изучения. Ярким примером является интегральное исчисление. Данная область научных знаний представляет собой раздел анализа в математике. При решении подобных задач предстоит оперировать такими терминами, как первообразная, производная, дифференцирование и предел.

Каждое из перечисленных понятий обладает определенным смыслом и назначением, выражается уравнениями и свойствами. В результате детального разбора интегрирование не вызывает серьезных проблем. Нужно лишь разобраться в терминологии и освоить основные принципы выполнения вычислений. Например, для определения интеграла находят какое-либо число раз результат произведения некоторых слагаемых, а полученные итоговые значения суммируют друг с другом.

Однако в математической науке существует эффективный способ решения вышеописанных проблем. Предположим, что имеется какой-то произвольный велосипед, на который установили спидометр. Пусть этот прибор замеряет параметры скорости и фиксирует эту величину в определенные временные промежутки. По итогам измерений формируется график, описывающий передвижение велосипедиста.

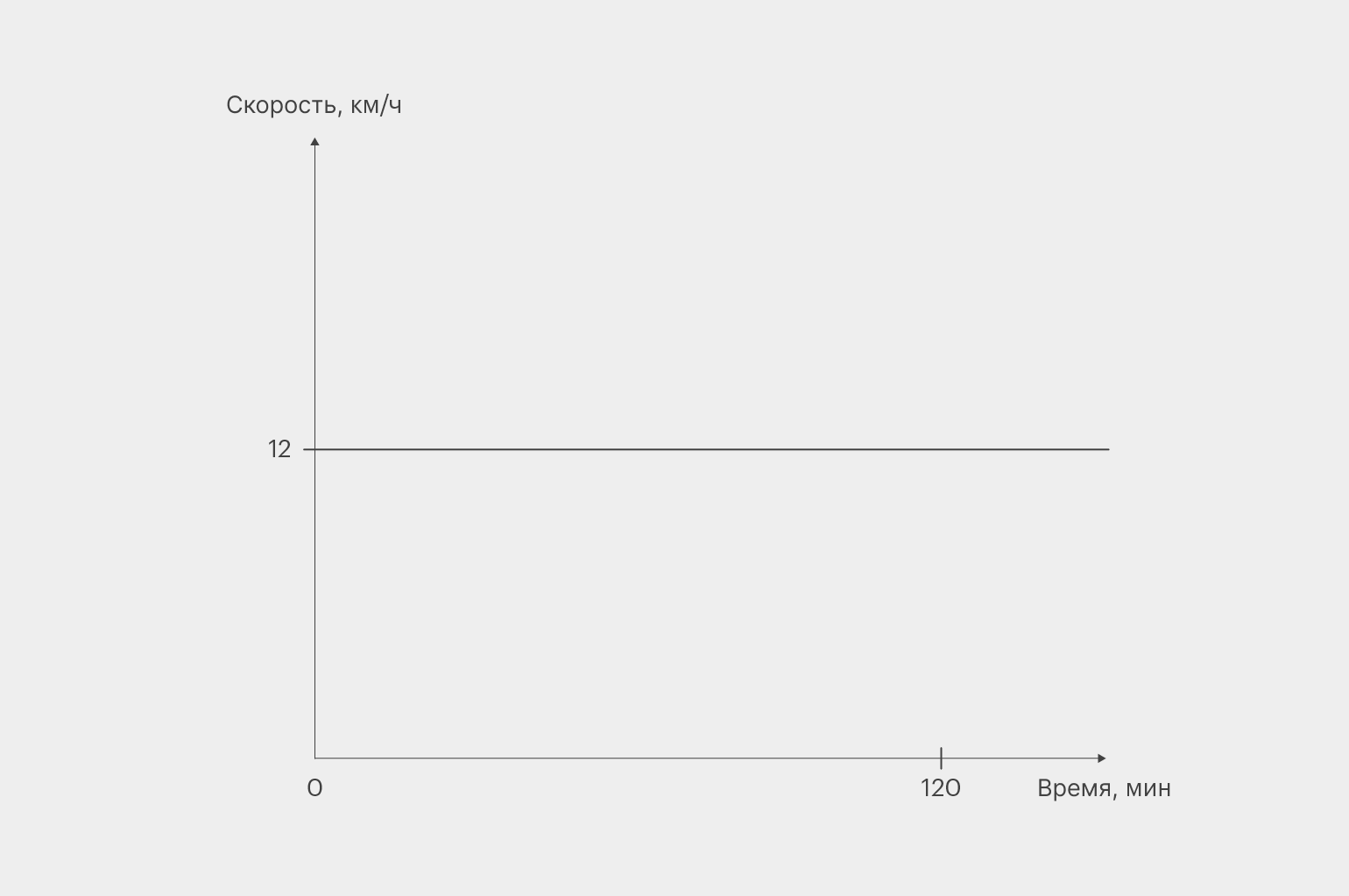
Введем числовые обозначения рассматриваемых физических величин. Начальную точку пути допустимо обозначить за А, а конечный пункт назначения можно назвать точкой Б. Время в пути составляет пару часов при усредненном скоростном параметре, равном 12 км/ч. Это приблизительные значения, которые зафиксированы по субъективному мнению велосипедиста. Представим на рисунке ниже график движения.

Источник: skillbox.ru

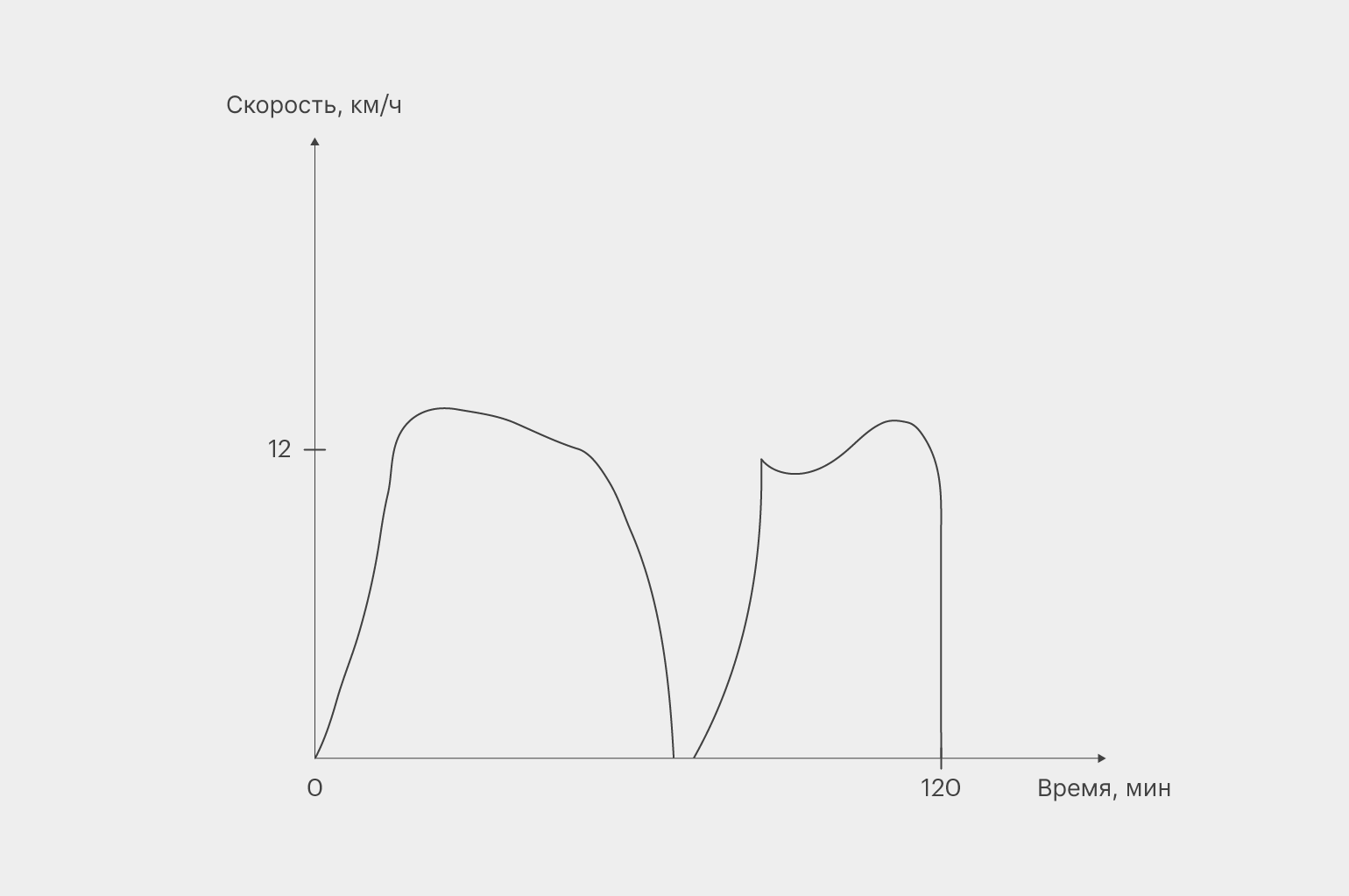
С целью вычислить преодоленный путь следует умножить время в пути на скорость. По итогам простых расчетов получится расстояние в 24 км. Однако в реальном мире это путешествие выглядит иначе. Например, в самом начале пути велосипедист замедляется, затем набирает скорость и продолжает разгон до следующего замедления. Подобные периоды с некоторой вероятностью повторяются, а стадии перемещения могут меняться местами. Представим, что на практике движение реализовано таким образом:

Источник: skillbox.ru

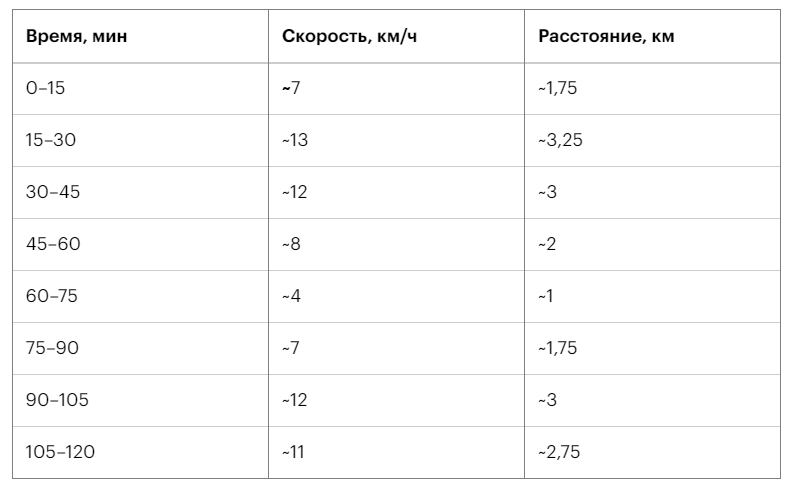
Теперь вычислить расстояние, которое преодолел велосипедист, значительно труднее. Это обусловлено изменениями скоростных параметров в разные временные интервалы. Подобную задачу несложно решить, если воспользоваться действенной методикой, то есть нужно найти результат усредненной скорости путем деления общего времени на одинаковые интервалы. Определим искомые величины для четверти часа. С этой целью найдем итог умножения такого периода на приблизительную скорость. Перепишем полученный путь для каждого случая в табличную форму:

 

Источник: skillbox.ru

По итогам сложения перечисленных в таблице отрезков пути получается расстояние, которое составляет около 18,5 км. Однако из-за примерного расчета средней скорости результат представлен тоже с погрешностью. Увеличить степень точности ответа целесообразно с помощью изучения большего количества временных периодов, к примеру, взять за основу не 15 минут, а 1 минуту или 1 секунду. Уменьшение интервала времени, который участвует в вычислениях, приводит к получению более точных результатов.

Идеальный вариант решения заданного выше примера заключается в делении графического представления движения велосипедиста на такое количество интервалов, которое стремится к бесконечности. При этом размер любого из промежутков приближается к нулевому значению. Продолжить вычисления в таких условиях можно с помощью поиска результата от произведения всех интервалов и последующего суммирования полученных значений. Это не отличается от предыдущего алгоритма действий, за исключением таблицы, которую невозможно измерить. Таким образом, получен интеграл рассматриваемой функции, выраженный следующей формулой:

\(\int f(x)dx\)

В записи \int обозначает интеграл, f(x) является интегрируемой функцией, dx свидетельствует о бесконечно маленьких интервалов, которые использованы в проведении расчетов.

С помощью наглядного примера из жизни получилось сформировать некоторую функцию, используя интеграл, при единственной известной величине в виде производной. Данная функция после восстановления является первообразной. При этом интеграл, необходимый для ее вычисления, носит название неопределенного. Такое название связано с особенностью представления целой функции, а не какого-либо определенного числа.

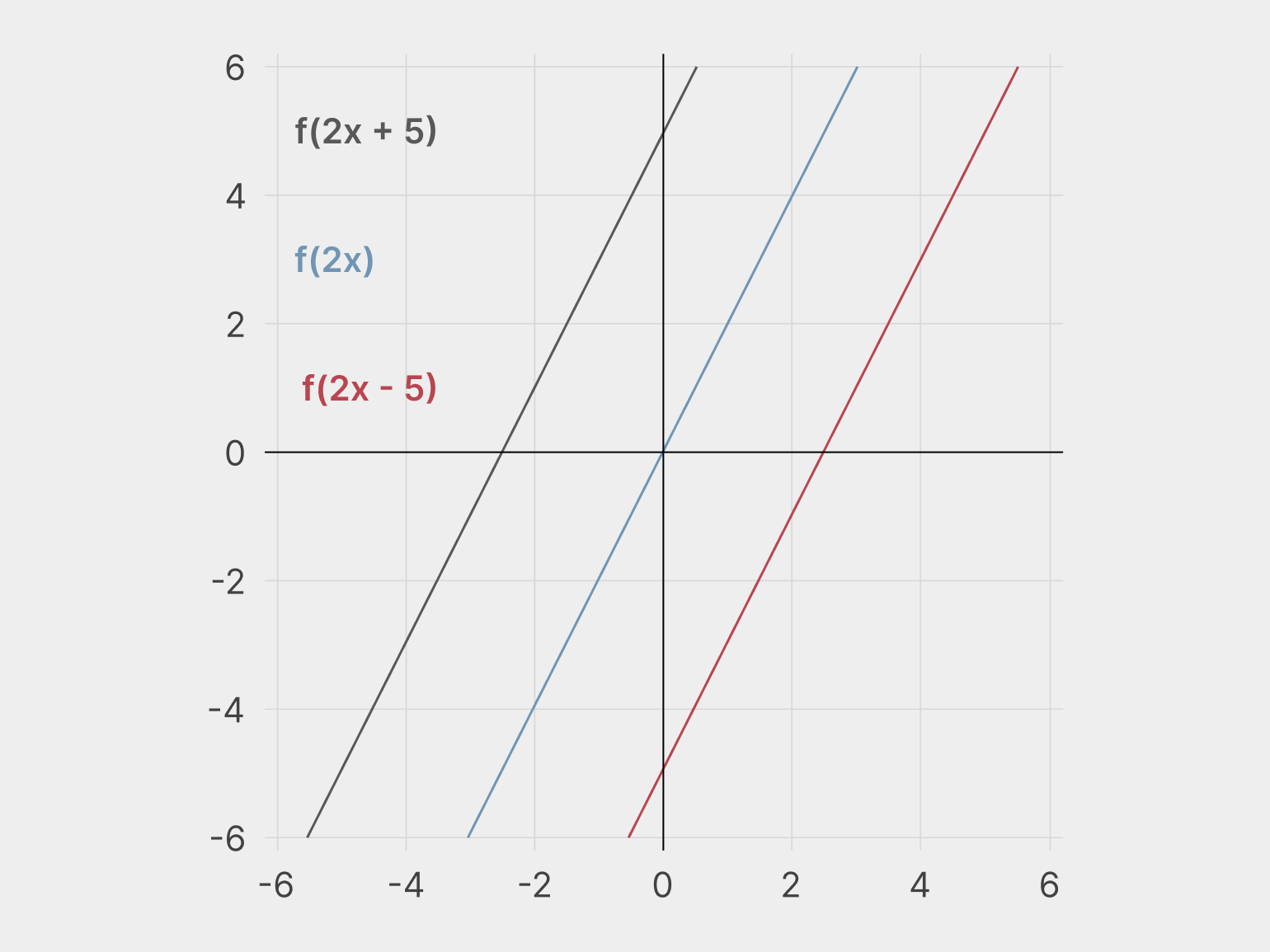
Неопределенный интеграл обладает способностью к возврату не единственной первообразной, а их комплекса. В качестве следующего примера рассмотрим сразу три первообразные f(2x), f(2x + 5) и f(2x − 5). Представим на одной координатной плоскости их графические изображения:

Источник: skillbox.ru

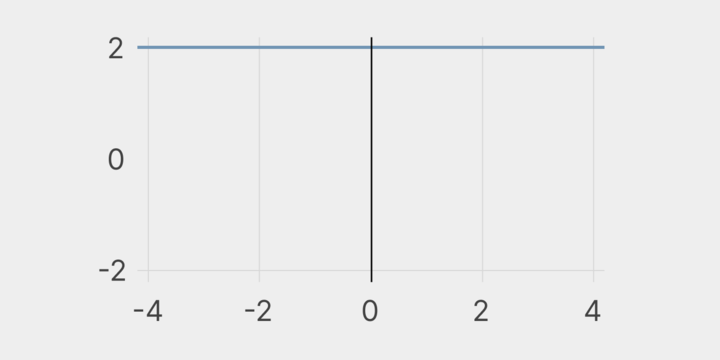
На следующем этапе нужно выполнить дифференцирование функций и вычислить, чему равны их производные. В каждом примере результат одинаковый и составляет F(2). Таким образом, у = 2.

Источник: skillbox.ru

Исходя из проделанных расчетов, можно заметить рост рассматриваемых функций с равными скоростями. В процессе увеличения на одно деление по оси абсцисс возрастает на два деления по оси ординат. Таким образом, анализируемые функции имеют одинаковую производную.

Интегрирование представляет собой обратное действие относительно дифференцирования. При взятии интеграла от F(2) в результате получаются такие значения, как f(2x), и f(2x + 5), и f(2x − 5). Перечисление допустимо продлить на бесконечное число прочих функций аналогичного вида. Такое дополнительное число представляет собой произвольную постоянную, которую обязательно записывают в итоговом результате, то есть f(2x + C).

Обобщенный вид записи неопределенного интеграла имеет следующий вид:

\(\int f(x)dx = F(х) + С\)

В том случае, когда f(x) имеет какое-либо определение и не прерывается на отрезке от а до b, и F(x) представляет собой первообразную данной функции, то есть справедливо равенство \(F'(x)=f(x)\) при условии, что a<x<b, то верным является следующее соотношение:

\(\int f(x)dx=F(x)+C,\)

a<x<b, где С определена, как произвольная постоянная.

Свойства

Если по итогам рассмотрения практических примеров с пониманием основных терминов проблем не возникает, то при решении задач можно столкнуться с массой сложных расчетов и математических преобразований. Из теоретического курса алгебры известно, что для любого действия несложно найти максимально эффективный и рациональный способ вычислений. Задания на неопределенный интеграл не являются исключением. Значительно упростить и сократить ход решения можно, применяя специальные свойства. Такие закономерности позволяют успешно справляться с самыми сложными задачами. Перечислим основные из них:

\(d\left(\int f(x)dx\right)=f(x)dx\)

\(\int d(F(x))=F(x)+C\)

\(\int a\cdot f(x)dx=a\cdot \int f(x)dx,a\neq 0\)

\(\int (f(x)\pm g(x))dx=\int f(x)dx\pm \int g(x)dx\)

\(\int f(x)dx=F(x)+C \Rightarrow \int f(u)du=F(u)+C\)

В записи \(u=\varphi (x)\) играет роль произвольной функции, которая обладает непрерывной производной.

Таблица неопределенных интегралов

Следующий действенный способ упростить задачу по нахождению неопределенного интеграла состоит в использовании специальной таблицы. В такой форме представлены значения первообразных функций. Приведем наглядные примеры в виде справедливых равенств, где с левой стороны расположена какая-то определенная первообразная функция для конкретной функции под знаком интеграла. С другой стороны записана одна определенная первообразная, суммированная с константой. При этом С обладает таким значением, что выражение обращено в верное равенство.

\(\int 0\cdot dx=C\)

\(\int 1\cdot dx=x+C\)

\(\int x^{n}dx={\frac {x^{n+1}}{n+1}}+C, (n\neq -1)\)

\(\int {\frac {1}{x}}dx=\ln \mid x\mid +C\)

\(\int e^{x}dx=e^{x}+C\)

\(\int a^{x}dx={\frac {a^{x}}{\ln a}}+C, (a>0,a\neq 1)\)

\(\int \cos x\,dx=\sin x+C\)

\(\int \sin x\,dx=-\cos x+C\)

\(\int {\frac {dx}{\cos ^{2}x}}=\mathrm {tg} \,x+C\)

\(\int {\frac {dx}{\sin ^{2}x}}=-\mathrm {ctg} \,x+C\)

\(\int {\frac {dx}{\sqrt {1-x^{2}}}}=\arcsin x+C_{1}=-\arccos x+C_{2}\quad (C_{2}={\frac {\pi }{2}}+C_{1})\)

\(\int {\frac {dx}{1+x^{2}}}=\mathrm {arctg} \,x+C\)

\(\int \mathrm {ch} \,xdx=\mathrm {sh} \,x+C\)

\(\int \mathrm {sh} \,xdx=\mathrm {ch} \,x+C\)

Как вычислить

Сложно решать задачи на интегрирование с неопределенными интегралами, используя лишь обобщенную формулу для проведения расчетов. Тогда вычисления получаются громоздкими, отнимают массу сил и времени. Ситуация меняется, если знать несколько приемов интегрирования. Существует ряд верных математических соотношений, с помощью которых достаточно просто найти ответ к той или иной задаче. К примеру, когда необходимо записать выражение под знаком дифференцирования, следует обратиться к следующим свойствам:

du=d(u+C)

\(du={1 \over a}d(au)\)

\(f'(u)\cdot du=d(f(u))\)

В случае необходимости в вычислении неопределенного интеграла целесообразно воспользоваться стандартными методиками выполнения расчетов:

1. Использование нового аргумента. Если \(\int g(x)dx=G(x)+C, то \int g(u)du=G(u)+C, где u=\varphi (x)\) является функцией, которая не прерывается и дифференцируется.
2. Способ разложения. Если \(g(x)=g_{1}(x)+g_{2}(x), то \int g(x)dx=\int g_{1}(x)dx+\int g_{2}(x)dx\).
3. Способ подстановки. Если g(x) не прерывается, то, зная, что \(x=\varphi (t), где \varphi (t) \) не прерывается, как и ее производная \(\varphi '(t)\), получим \(\int g(x)dx=\int g(\varphi (t))\varphi '(t)dt.\)
4. Способ частичного интегрирования. При произвольных дифференцируемых функциях u и v от х справедливо следующее равенство \(\int udv=uv-\int vdu.\)

Примеры решения задач

После освоения теоретического материала остается закрепить знания путем решения практических примеров. В процессе целесообразно руководствоваться стандартным алгоритмом действий. Начать стоит с анализа условий задания, что поможет быстро выявить известные и неизвестные величины. Далее функцию под знаком интеграла необходимо преобразовать для получения какой-либо из функций, представленных в табличной форме. В том случае, когда этот способ не работает с какой-то определенной задачей, допустимо воспользоваться методикой внесения под дифференциал, способом замены переменной или частичного интегрирования в зависимости от специфики сложившейся ситуации.

Решение

В первую очередь следует обратить внимание на условия задания. Заметим, что в данном случае целесообразно воспользоваться свойством интегралов. В процессе вычислений потребуется выполнить замену интеграла суммы на сумму интегралов с последующей записью коэффициентов за пределами знака интеграла:

\(\int \left( 6x^{7}+4 \sqrt[5]{x^{3}} + \frac{3}{x^{4}} +1 \right) dx = 6 \int x^{7} dx + 4 \int \sqrt[5]{x^{3}} dx + 3 \int \frac{dx}{x^{4}} + \int dx\)

Выполним преобразование степени переменных:

\(\int \left( 6x^{7}+4 \sqrt[5]{x^{3}} + \frac{3}{x^{4}} +1 \right) dx = 6 \int x^{7} dx + 4 \int x^{\frac{3}{5}} dx + 3 \int x^{-4} dx + \int dx\)

Далее можно воспользоваться табличной формой с интегральными значениями. В результате получим:

\(\int \left( 6x^{7}+4 \sqrt[5]{x^{3}} + \frac{3}{x^{4}} +1 \right) dx = 6 \int x^{7} dx + 4 \int x^{\frac{3}{5}} dx + 3 \int x^{-4} dx + \int dx = 6 \cdot \frac{x^{7+1}}{7+1} + 4 \cdot \frac{x^{\frac{3}{5}+1}}{\frac{3}{5}+1} + 3 \cdot \frac{x^{-4+1}}{-4+1} + x + C = \frac{6 \cdot x^{8}}{8} + \frac{4 \cdot x^{\frac{8}{5}}}{\frac{8}{5}} + \frac{3 \cdot x^{-3}}{-3}+x+C=\frac{3}{4}x^{8} + \frac{5}{2} \sqrt[5]{x^{8}} - \frac{1}{x^{3}}+x+C\)

Ответ: \(\int \left( 6x^{7}+4 \sqrt[5]{x^{3}} + \frac{3}{x^{4}} +1 \right) dx = \frac{3}{4}x^{8} + \frac{5}{2} \sqrt[5]{x^{8}} - \frac{1}{x^{3}}+x+C\)

 

Решение

Вновь начнем решать задачу с анализа условий. Заметим, что в данном случае целесообразно в первую очередь приступить к преобразованию выражения со сложением, расположенного в числителе:

\(\int \frac{2x^{2}+1}{x^{2}(x^{2}+1)} dx = \int \frac{x^{2}+(x^{2}+1)}{x^{2}(x^{2}+1)} dx\)

Далее последний интеграл допустимо разделить на сумму пары интегралов. С этой целью нужно поделить каждый член числителя на знаменатель:

\(\int \frac{2x^{2}+1}{x^{2}(x^{2}+1)} dx = \int \frac{x^{2}}{x^{2}(x^{2}+1)} dx + \int \frac{x^{2}+1}{x^{2}(x^{2}+1)} dx = \int \frac{dx}{x^{2}+1} + \int \frac{dx}{x^{2}} = \int \frac{dx}{x^{2}+1} + \int x^{-2} dx\)

Нужно обратить внимание на пару последних интегралов. Значения этих выражений легко выписать из табличной формы. В результате получим:

\(\int \frac{2x^{2}+1}{x^{2}(x^{2}+1)} dx = \int \frac{dx}{x^{2}+1} + \int x^{-2} dx = \text{arctg } x + \frac{x^{-2+1}}{-2+1} + C = \text{arctg } x - \frac{1}{x} + C\)

Ответ: \(\int \frac{2x^{2}+1}{x^{2}(x^{2}+1)} dx = \text{arctg } x - \frac{1}{x} + C\)

 

Решение

В этом случае стоит начать с записи единой степени х за пределами скобок. Сделать это можно следующим способом:

\(\int 2^{x} \cdot 3^{2x} dx = \int \left( 2 \cdot 3^{2} \right)^{x} dx = \int \left( 2 \cdot 9 \right)^{x} dx = \int 18^{x} dx\)

Получим в результате несложных вычислений интеграл из таблицы. Продолжим соответствующие расчеты:

\(\int 2^{x} \cdot 3^{2x} dx = \int 18^{x} dx = \frac{18^{x}}{\ln 18} + C\)

Ответ: \(\int 2^{x} \cdot 3^{2x} dx = \frac{18^{x}}{\ln 18} + C\)

Решение

Заметим, что рассматриваемый интеграл не получится решить с помощью таблицы. Однако при замене переменной на 2х + 1 допустимо представить функцию, расположенную под знаком интеграла, в виде степенной. В связи с этим, данная задача решается путем применения методики внесения под дифференциал. В результате записанных манипуляций получим следующее:

\(d(2x+1)=2 dx \text{ } \Rightarrow \text{ } dx = \frac{d(2x+1)}{2}\)

\(\int (2x+1)^{4} dx = \frac{1}{2} \int (2x+1)^{4} d(2x+1)\)

Продолжим вычисления со степенной функцией:

\(\int (2x+1)^{4} dx = \frac{1}{2} \int (2x+1)^{4} d(2x+1) = \frac{1}{2} \cdot \frac{(2x+1)^{4+1}}{4+1} + C = \frac{(2x+1)^{5}}{10} + C\)

Ответ: \(\int (2x+1)^{4} dx = \frac{(2x+1)^{5}}{10} + C\)

Решение

Заметим, что в рамках решения данной задачи отсутствует возможность для преобразования интеграла с применением простейших значений из стандартной таблицы. Тогда следует прибегнуть к способу замены переменной, а именно \(-x^{2}=t\). В результате получим:

\(-2x dx = dt \text{ } \Rightarrow \text{ } x dx = -\frac{dt}{2}\)

Путем подстановки нового значения в начальную запись интеграла выполним следующие преобразования:

\(\int x e^{-x^{2}}dx = -\frac{1}{2} \int e^{t} dt = -\frac{1}{2}e^{t} + C\)

Путем обратной замены \( t=-x^{2}\) вычислим искомое значение и запишем окончательный ответ:

\(\int x e^{-x^{2}}dx = -\frac{1}{2}e^{t} + C = -\frac{1}{2}e^{-x^{2}} + C\)

Ответ: \(\int x e^{-x^{2}}dx = -\frac{1}{2}e^{-x^{2}} + C\)