Дроби

Что такое дробь 

Дробь — это число, состоящее из одной или нескольких частей единицы. Обыкновенные дроби записываются в формате \(\frac mn\), где «—» — это дробная черта; n — знаменатель; а m — числитель. Такая запись читается как «m-энных».

Дроби нужны для обозначения нецелых количеств. Они образуются как результат деления натуральных чисел, когда делимое не кратно делителю.

Дробная черта равносильна знаку деления. То есть \(4:6=\frac46\) (четыре шестых), \(7:2=\frac72\) (семь вторых). Числитель дроби играет роль делимого, а знаменатель — делителя.

Знаменатель дроби не может быть нулем.

Основные свойства дробей

1. Дробь является видом записи числа. Одно и то же число можно записать в виде разных дробей.
2. Если умножить числитель и знаменатель на одинаковую величину, то значение дроби останется прежним, хотя дроби разные: \(\frac pr=\frac{c\cdot p}{c\cdot r}.\)
   Например, \(\frac34=\frac68=\frac9{12}.\)
3. И обратно, если числитель и знаменатель имеют общий делитель, то обе части можно разделить на него. Такая операция называется сокращением дроби: \(\frac{12}{16}=\frac{12:4}{16:4}=\frac34.\)

Виды

Существует два вида дробей: правильные и неправильные. 

Неправильные дроби всегда больше правильных: \(\frac{39}{40}<\frac32, \frac67<\frac33.\)

Правильные дроби

Правильная дробь называется так, поскольку выражает «правильную» часть единицы, то есть часть, которая меньше целого:\( \frac25<1, \frac{99}{100}<1.\)

Пример:

Рассмотрим дробь \(\frac56\), у которой 5 — это числитель, а 6 — знаменатель.Сравним числитель со знаменателем: 5<6. Так как числитель меньше знаменателя, дробь является правильной.

Неправильные дроби

Неправильная дробь — это обыкновенная дробь, числитель которой больше или равен знаменателю. Эти дроби всегда больше или равны единице: \(\frac73>1, \frac{14}8>1, \frac55=1.\)

Пример:

Рассмотрим дробь \(\frac65\), у которой 6 — это числитель, а 5 — знаменатель. 6>5, значит, данная дробь является неправильной.

Таким образом, отличить правильную дробь от неправильной можно при сравнении дробей с единицей. Это различие не влияет на арифметические действия, но важно при сравнении дробей.

Смешанные дроби

Неправильные дроби не принято оставлять в результате вычислений. Лучше преобразовывать их в смешанные числа. Любую неправильную дробь можно представить в виде смешанного числа.

Для составления смешанной дроби необходимо:

1. Выделить наибольшее целое число, содержащееся в неправильной дроби. Для этого нужно разделить числитель на знаменатель. Получившееся частное без остатка является целой частью смешанной дроби: \(\frac{40}5=40:5=8\).
2. Если в результате деления есть остаток, то этот остаток становится числителем дробной части. Знаменатель дробной части останется частным. \(\frac{42}5=8\frac25\)

Задача

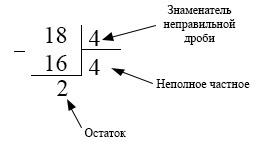
Записать неправильную дробь \(\frac{18}4\) в виде смешанной.

Решение

Выделим целую часть смешанной дроби. Чтобы сделать это, необходимо числитель дроби, 18, поделить на ее знаменатель, 4:
Итак, получаем, что \(\frac{18}4=18:4=4\), остаток 2.

Тогда искомая смешанная дробь \(\frac{18}4=4\frac24.\) Эту дробь можно сократить, поделив числитель и знаменатель дробной части на общий делитель 2:

\(4\frac24=4\frac{2:2}{4:2}=4\frac12\)

Ответ: \(4\frac12.\)

Примечание

Смешанное число можно записать в виде неправильной дроби. Для этого необходимо целую часть умножить на знаменатель дробной части. К полученному числу нужно прибавить числитель дробной части. Эту сумму записать в числитель, а знаменатель дробной части оставить без изменений.

Задача

Смешанное число \(6\frac25\) записать в виде неправильной дроби.

Решение

\(6\frac25=\frac{6\cdot5+2}5=\frac{32}5\)

Ответ: \(\frac{32}5\)

Как перевести правильную дробь в неправильную

Перевести правильную дробь в неправильную или наоборот невозможно. Это разные категории чисел.

Любое натуральное число можно представить в виде неправильной дроби: \(2=\frac21.\)

Дробь с числителем p и знаменателем 1 — это другая форма записи натурального числа p. Это правило можно представить в виде формулы: \(p=\frac p1.\)

Число 0 считают равным дроби вида \(\frac0q\), где q — любое натуральное число:

\(0=\frac01=\frac02=\dots=\frac0q\)

Действия с дробями, как решать примеры

Приведение к общему знаменателю

Определение

Чтобы решать большинство примеров с дробями, необходимо приводить их к общему знаменателю. Чтобы привести дроби \(\frac ab\) и \(\frac cd\) к общему знаменателю, необходимо:

1. Найти наименьшее общее кратное (НОК) обоих знаменателей: \(M=\left[b,d\right].\)
2. Умножить числитель и знаменатель первой дроби на M/b: \(\frac{a\cdot\frac Mb}{b\cdot\frac Mb}.\)
3. Умножить числитель и знаменатель второй дроби на M/d: \(\frac{c\cdot\frac Md}{d\cdot\frac Md}.\)

Пример:

Необходимо привести к общему знаменателю дроби \(\frac34\) и \(\frac13\). Действуем по алгоритму:

1. Находим НОК. У чисел 4 и 3 им является число 12.
2. Умножаем числитель и знаменатель первой дроби на \(\frac{12}4\), то есть 3: \(\frac{3\cdot3}{4\cdot3}=\frac9{12}\).
3. Умножаем числитель и знаменатель второй дроби на \(\frac{12}3\), то есть 4: \(\frac{1\cdot4}{3\cdot4}=\frac4{12}\).

Ответ: \(\frac9{12}, \frac4{12}.\)

Сравнение

Пример:

\(\frac34>\frac13,\) поскольку \(\frac9{12}>\frac4{12}.\)

К примеру, \(8\frac16>5\frac23.\)

Если целые части смешанных чисел равны, то сравнивают дробные части по правилу сравнения обыкновенных дробей. Число с наибольшей дробной частью будет больше: \(5\frac23>5\frac13.\)

Сложение и вычитание

Пример:

\(\frac34+\frac13=\frac9{12}+\frac4{12}=\frac{13}{12}=1\frac1{12}\)

\(5\frac13+4\frac16=9\frac{2\cdot1+1}6=9\frac36=9\frac12\)

Пример:

\(\frac12-\frac13=\frac{3-2}6=\frac16\)

Умножение и деление

\(\frac ab\cdot\frac cd=\frac{ac}{bd}\)

Задача

Умножить дробь \(\frac35\) на \(\frac23.\)

Решение

\(\frac35\cdot\frac23=\frac{3\cdot2}{5\cdot3}=\frac6{15}=\frac25\)

Ответ: \(\frac25\)

При умножении дроби на натуральное число, нужно умножить числитель на это число, а знаменатель оставить тем же. Так происходит, поскольку любое натуральное число можно представить в виде \(p=\frac p1.\)

\(\frac ab\cdot p=\frac ab\cdot\frac p1=\frac{ap}b.\)

\(2\frac13\cdot3\frac12=\frac73\cdot\frac72=\frac{49}6=8\frac16\)

\(\frac ab:\frac cd=\frac ab\cdot\frac dc=\frac{ad}{bc}.\)

Задача

Поделить дробь \(\frac34\) на \(\frac23.\)

Решение

\(\frac34:\frac23=\frac34\cdot\frac32=\frac{3\cdot3}{4\cdot2}=\frac98=1\frac18\)

Ответ: \(1\frac18\)

\(2\frac13:1\frac16=\frac73:\frac76=\frac{7\cdot6}{3\cdot7}=\frac63=2\)