Объединение множеств

Что такое объединение и пересечение множеств А и Б

Оно может состоять из чисел, букв, прямых, точек, слов и т.д. Эти объекты, которые совокупно образуют данное множество, являются его элементами или точками.

Для обозначения множеств применяют заглавные буквы латинского алфавита. А их элементы обозначают строчными буквами. Например, запись\( x\in K\) означает, что х является элементом множества \(К.\)

Если множества А и Б содержат одинаковые элементы, то они равны:

\(А\;\subset\;Б\) и \(Б\;\subset\;А.\)

Если множество не содержит в себе ни одного элемента, то оно называется пустым и является подмножеством любого множества. Оно обозначается символом \(Ø.\)

Если пустое множество пересекается с другим, то их общее множество будет так же пустым:

\(A\;\cap\;Б\;=\;\varnothing.\)

Если множества равны, то всякий элемент х, принадлежащий правой части равенства, принадлежит и левой, и наоборот.

 Основные операции с множествами подразделяются на:

• пересечение;
• объединение;
• вычитание;

Понятие и свойства объединения множеств

Объединение С множеств А и Б обозначается таким образом:

\(C=A\cup Б\)

\(A\;\cap\;Б\;=\;\left\{\left.х\right|\;х\in\;А\;или\;х\;\in\;Б\right\}.\)

A = {2; 3; 6; 8} и Б = {4; 6; 8; 9}.

Тогда их объединением будет служить множество С = {2; 3; 4; 6; 8; 9}.

Свойства объединений:

Некоторые свойства операции объединений напоминают по своему принципу привычную операцию «сложения» чисел. При этом некоторые свойства объединения, которые соответствуют определенным операциям сложения чисел, будут иметь свои особенности.

Свойства объединения, которые справедливы для любых множеств A, Б и C:

A U Б = Б U A; A U (Б U C) = (A U Б) U C.

\(А\subset А\cup Б\;и\;Б\subset А\cup Б.\)

Кроме того, из включения \(А\subset Б\) следует включение:

\(А\cup С\subset Б\cup С.\)

В частности, любому множеству A соответствует равенство:

\(А\cup А=А.\)

Это равенство означает идемпотентность объединения, то есть повторное осуществление операции по отношению к объекту будет давать тот же результат, что и в первый раз.

А также равенство:

\(А\cup\varnothing=А.\)

Если у множеств А и Б есть общие элементы, то каждый из этих элементов не повторяется в объединении, и входят в него один раз.

Понятие и свойства пересечения множеств

Пресечение множеств обозначают символом \(∩\):

\(С=А\cap Б\)

\(А\cap Б=\left\{\left.х\right|\;х\in А\;и\;х\in Б\right\}.\)

A = {2; 3; 6; 8} и Б = {4; 6; 8; 9}; тогда их пересечением будет являться C = {6; 8}.

Свойства пересечений:

Некоторые свойства операции пересечений напоминают по своему принципу привычную операцию «умножения» чисел. При этом некоторые свойства пересечения, которые соответствуют определенным операциям умножения чисел, будут иметь свои особенности.

Свойства пересечения, которые справедливы для любых множеств A, B и C:

A ∩ Б = Б ∩ A; A ∩ (Б ∩ C) = (A ∩ Б) ∩ C.

\(А\cap Б\subset А\;и\;А\cap Б\subset Б.\)

Если у множеств А и Б нет общих элементов, то их пересечением является пустое множество, иначе говорят, что они не пересекаются.

Кроме того, из включения \(А\subset Б\) следует включение:

\(А\cap С\subset Б\cap С.\)

В частности, для любого множества A имеет место равенство\( А\cap\varnothing=\varnothing.\)

Также верно равенство \(А\cap А=А.\)

Здесь, как и в объединении, встречается свойство идемпотентности пересечения. Поэтому здесь не говорят о возведении множества в степени в том привычном смысле, какое применимо к степени числа. Этим операция пересечения отличается от операции умножения чисел, что легко доказывается на различных множествах.

Для произвольной совокупности множеств \(А_\alpha\), где α относится ко всем элементам множества I, \(А_\alpha,\;\alpha\in I\), пишут в случае объединения:

\(C=\underset{\alpha\in I}\cup A_\alpha=\underset\alpha\cup A_\alpha;\)

в случае пересечения:

\(C=\underset\alpha\cap A_\alpha.\)

Правила нахождения пересечений и объединений, формулы

Конечное множестве А обладает мощностью, представляющей собой число элементов. Его обозначают как \(|А|\) или #А.

Если известны мощности каждого множества и их пересечений, то по следующей формуле можно найти мощность объединения:  

\(\left|А\cup Б\right|=\left|А\right|+\left|Б\right|-\left|А\cap Б\right|;\)

\(\left|А\cup Б\cup С\right|=\left|А\right|+\left|Б\right|+\left|С\right|-\left|А\cap Б\right|-\left|А\cap С\right|-\left|Б\cap С\right|+\left|А\cap Б\cap С\right|.\)

Вообще  \(\left|А_1\cup...\cup А_n\right|\) равно

\(\sum_i\left|A_i\right|-\sum_{i<J}\left|A_i\cap A_j\right|+\sum_{i<J<k}\left|A_i\cap A_j\cap A_k\right|-....\)

Она называется формулой включений и исключений.

Доказательство

Чтобы доказать это утверждение зафиксируем произвольное множество К. Его подмножествами являются \(A_1,...,A_n.\) Функция \(X_x\) является характеристической функцией множества \(X\subset K\). На элементах Х она равна 1, а на остальных элементах К — равна нулю. Проводимые над подмножествами множества К операции соответствуют операциям с их характеристическими функциями.

В частности, произведение характеристических функций соответствует пересечению множеств:

\(X_{A\cap B}(u)=X_A(u)X_B(u).\)

Если Х является характеристической функцией исходного множества, то дополнению (до К) соответствует функция 1 — Х.

Запишем в виде суммы значений характеристической функции число элементов множества:

\(\left|x\right|=\sum_uX_x(u).\)

Объединение \(A_1\cup...\cup A_n\) представим в виде дополнения к пересечению дополнений множеств \(A_i.\)

Опираясь на термины характеристических функций, получим:

\(X_{A_1\cup...\cup A_n}=1-(1-X_{A_1})...(1-X_{A_n}).\)

Раскроем скобки в правой части:

\(\sum_iX_{A_i}-\sum_{i<j}X_{A_i}X_{A_j}+\sum_{i<j<k}X_{A_i}X_{A_j}X_{A_k}-....\)

Получим формулу включений и исключений, просуммировав правую и левую части по всем элементам К. которые являются функциями на К.

Исследование множеств с помощью координатной прямой

Для любого натурального числа на координатной прямой можно выбрать соответствующую только ему единственную точку. Каждому числу на данной прямой можно подобрать противоположное число, которое расположено симметрично относительно начала отсчета и отличается от другого только знаком.

Также каждому действительному (рациональному или иррациональному) на координатной прямой соответствует единственная точка и, наоборот, для каждой ее точки есть единственное действительное число. Это называется взаимно однозначным соответствием. С учетом этого соответствия,множество R действительных чисел и множество точек координатной прямой часто объединяют общим термином — «числовая прямая».

Ось Оу образована множеством точек х = 0, поэтому ось Оу является графиком уравнения х — 0.

Ось Ох образована множеством точек у = 0, поэтому ось Ох является графиком уравнения у — 0.

Множество точек у = х образует прямую, которая проходит через начало координат и делит I и III квадранты пополам.

В математике есть важное понятие упорядоченной пары (х, у), которое представлено либо элементами одного и того же множества, либо элементами разных множеств Х и У.

Свойством упорядоченных пар является то, что две упорядоченные пары (\(x_1, y_1)\) и \( (x_2)\) и \((y_2)\) будут называться равными, когда \( x_1=x_2\ и\ y_1=y_2.\)

Первой компонентой (координатой) пары (х, у) является элемент х, второй компонентой (координатой) той же пары — элемент у.

Понятие упорядоченной пары поваляет ввести дополнительную операцию над множествами — прямое или декартово умножение, имеющее вид:

\(X\times Y=\left\{\left.(x,y)\right|\;x\in X,\;y\in Y\right\}\;.\)

Декартово произведение между двумя пересекающимися различными прямыми может быть отождествлено с проходящей через эти прямые плоскостью по правилу \(А = (х, у)\). Это свойство объясняет название умножения и является основой метода координат, который Рене Декартом предложил для решения геометрических задач.

Для определения упорядоченного набора n+1 элементов применяется метод математической индукции:

\((x_1,\;x_2,\;...,\;x_{n+1})=((x_1,\;x_2,\;...,\;x_n),\;x_{n+1}),\;n\geq2.\)

Отсюда выводится произведение множеств:

\(X_1\times X_2\times...X_{n+1}=(X_1\times X_2\times...\times X_n)\times X_{n+1}.\)

Чтобы установить между точками координатной прямой соответствие и между множеством натуральных чисел, на прямой выбирают произвольную точку 0, а затем с помощью единичного отрезка отмечают на ней точки, которым соответствуют натуральные числа.

Соответственно, чем правее число расположено на координатной прямой, тем оно больше.

Отсюда следует:

• всякое отрицательное число меньше числа, которое является положительным и больше нуля;
• всякое отрицательное число всегда меньше нуля;
• из двух отрицательных чисел меньше то, модуль которого больше, и наоборот. Например, -4,8 > -6,2, так как|-4,8| < |-6,2|.

Числовые промежутки на координатной прямой имеют обозначения:

1. \([a; b] = {x \in R | a ≤ x ≤ b}\) — замкнутый промежуток (или отрезок) с началом а и концом b.
2. \((a; b) = {x \in R | a < x < b}\) — открытый промежуток (или интервал).
3. \((a;\;b\rbrack=\{x\in R\vert\;a<x\leq b\};\;\lbrack a;\;b)\;=\;\{x\in R\vert\;a\leq x<b\}\) — полуоткрытые промежутки.
4. \((a;\;+\infty\rbrack=\{x\in R\vert\;x\geq a\};\;\lbrack-\infty;\;b)\;=\;\{x\in R\vert\;x\leq b\}\) — лучи.
5. \((a;\;+\infty)=\{x\in R\vert\;x>a\};\;(-\infty;\;b)\;=\;\{x\in R\vert\;x<b\}\) — открытые лучи.
6. \((-\infty;\;+\infty)\;=R\) — числовая прямая.

Как определить пересечение и объединение при помощи изображений числовых множеств

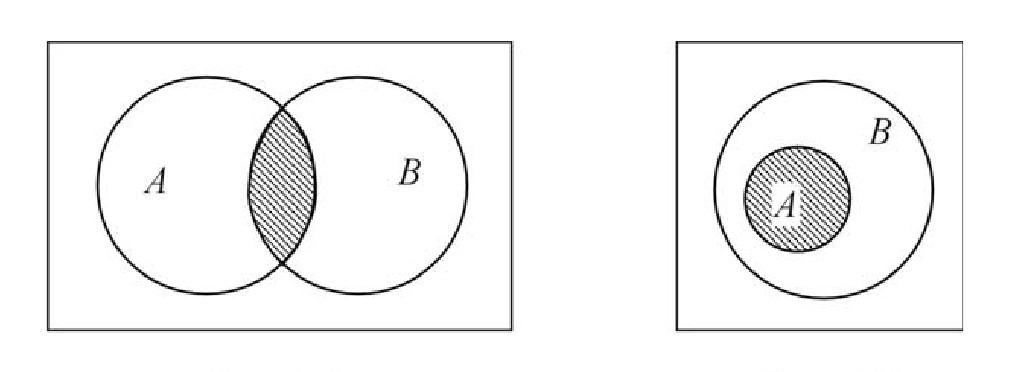
Взаимоотношения и операции между множествами можно наглядно проиллюстрировать, применяя диаграммы Эйлера-Венна. Множества в этих диаграммах чаще всего изображаются в виде кругов и их внутренностями, а в виде прямоугольника изображено универсальное множество U.

В диаграммах Эйлера-Венна имеет значение взаимное расположение, а не их относительный размер.

Изображение пересечения

Рисунки демонстрируют диаграммы Эйлера-Венна, описывающие два множества A и B в случаях, когда \(A\cap B\neq\varnothing\;и\;A\subset B\), соответственно. Множеству \(A\cap B\) на этих рисунках соответствуют части диаграмм со штриховкой.

Рисунок правее демонстрирует что, если A подмножество множества B,\( A\subset B,\;то\;A\cap B=A\), поскольку все элементы множества A будут общими для множеств A и B.

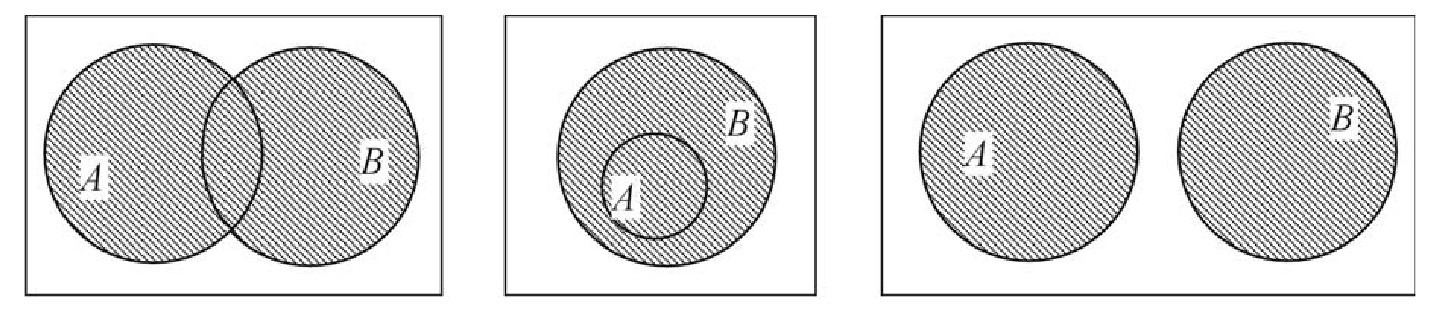
Изображение объединения

На рисунке представлены диаграммы Эйлера-Венна для двух множеств A и B в случаях, когда \(A\cap B\neq\varnothing,\;A\subset B\). Часть диаграммы со штрихами соответствует множеству \(A\cup B.\)

Рисунок демонстрирует, что если A подмножество множества B, т.е.

\(A\subset B,\;то\;A\cup B=B, \)

то раз включать элементы множества А в объединение не требуется, поскольку его элементы принадлежат и множеству B.

Основные законы операций объединения и пересечения множеств

Закон коммутативности

\(A\cup B=B\cup A,\;A\cap B=B\cap A.\)

Коммутативный закон показывает, что изменение порядка множеств в указанных операциях не влияет на их итог. Действительно, множества \(A\cup B\;и\;B\cup A\;\) состоят из элементов, которые относятся хотя бы к одному из множеств A или B, и не содержат никаких других элементов. А множества \(A\cap B\;и\;B\cap A\) включают в себя все элементы, относящиеся к каждому из множеств A и B.

Закон ассоциативности

\(A\cup(B\cup C)=(A\cup B)\cup C,\;A\cap(B\cap C)=(A\cap B)\cap C.\)

Ассоциативность указанных операций позволяет опускать фиксацию посредством скобок порядка проведения операций. Действительно, множества \(A\cup(B\cup C)\;и\;(A\cup B)\cup C\) состоят из всех элементов, входящих хотя бы в одно из множеств A, B и C и не содержат никаких других элементов, а множества \(A\cap(B\cap C)\;и\;(A\cap B)\cap C\) состоят только из общих элементов множеств A, B и C. Заметим, что по закону ассоциативности конечный результат не зависит от порядка действий. Но промежуточные результаты — зависят.

Закон дистрибутивности

\(A\cup(B\cap C)=(A\cup B)\cap(A\cup C),\;A\cap(B\cup C)=(A\cap B)\cup(A\cap C).\)

В числовом случае дистрибутивность умножения относительно сложения позволяет осуществлять вынос общего множителя за скобку и проводить раскрытие скобок. В случае множеств это так же справедливо, при этом соотношений такого рода больше.