Объем призмы
Что такое призма
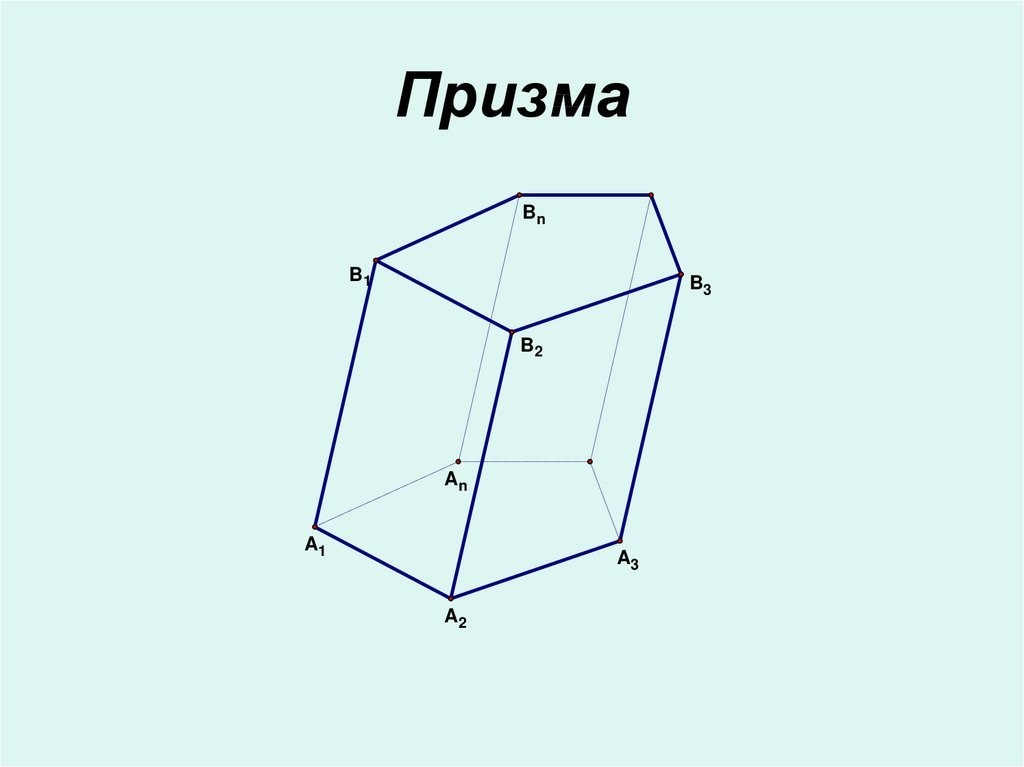
Призма — это трехмерное геометрическое тело с двумя равными основаниями и плоскими гранями. Название зависит от фигуры, которая лежит в ее основании. Например, если это треугольник, призму называют «треугольной».
Эта объемная фигура может быть нескольких видов:
- Прямая. То есть с боковыми ребрами, перпендикулярными основанию.
- Правильная. В основании лежит правильный многоугольник.
- Наклонная. Ее ребра расположены под углом к основанию.
Формулы вычисления объема правильной призмы
Правильные призмы могут быть разных видов, в зависимости от многоугольника, который лежит в их основании. Формула вычисления объема во всех случаях выглядит одинаково:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(V=S\cdot h\)
Разница лишь в том, каким образом находится площадь S для каждой из фигур.
Треугольная
Чтобы вычислить объем призмы, в основании которой лежит правильный треугольник, используем формулу:
\(V=\frac{\sqrt3}4\cdot a^2\cdot h\)
Где \(\frac{\sqrt3}4\cdot a^2=S\) — площадь правильного треугольника в основании, a — сторона треугольника, h — высота всей фигуры.
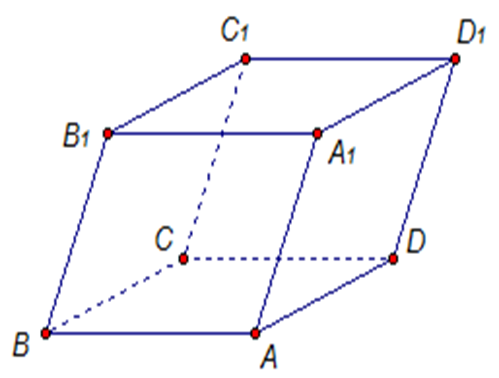
Четырехугольная
Для фигуры, в основании которой лежит квадрат, используем следующую формулу для вычисления объема:
\(V=a^2\cdot h\)
Где a — сторона квадрата.
Пятиугольная
В этом случае объем будет вычисляться по формуле:
\(V=\frac52\cdot a\cdot\sqrt{\left(\frac a{2\sin\left({\displaystyle\frac\pi5}\right)}\right)^2-\frac{a^2}4}\cdot h\\\)
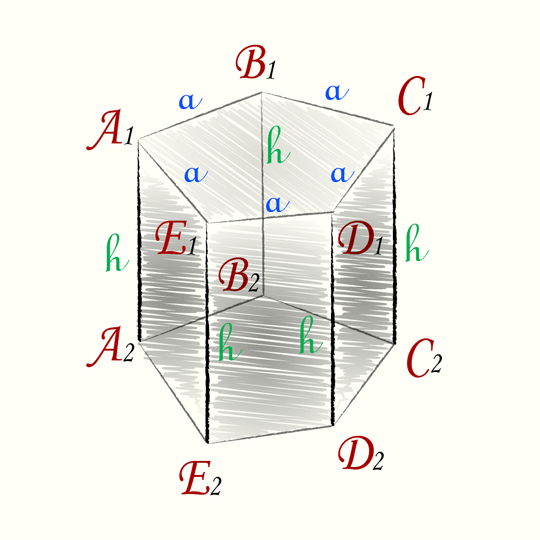
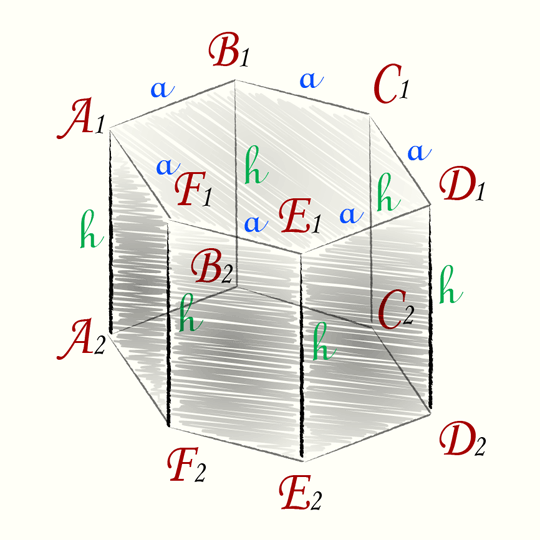
Шестиугольная
Для призмы с правильным шестиугольником в основании формула объема выглядит так:
\(x = V=\frac{3\sqrt3}2\cdot a^2\cdot h\\\)
Объем наклонной и прямой
Он находится через произведение площади основания на высоту:
\(V=S\cdot h\\\)
Таким образом, формула вычисления объема совпадает с предыдущими вариантами и зависит лишь от фигуры в основании.
С прямой призмой все то же самое. Сначала нужно вычислить площадь ее основания, а потом умножить на высоту.
Примеры задач
Известно, что площадь основания призмы равна 12 \(см^2\), а длина ее высоты — 5 см. Вычислить объем фигуры.
Решение:
Так как уже дана площадь основания, нам не важно какая фигура лежит в основании. Подставляем известные значения в формулу:
\(V=S\cdot h=12\cdot5=60 \) \(см^3\)
Ответ: V=60 \(см^3.\)
В основании прямой призмы лежит четырехугольник со сторонами a и b по 6 см и 3 см. Высота данной фигуры равна 10 см. Рассчитать ее объем.
Решение:
Так как сначала для вычисления объема нам нужно определить площадь четырехугольника, будем использовать уравнение: \(V=a\cdot b\cdot h\)
Подставляем значения: \(V=6\cdot3\cdot10=180\) \(см^3\)
Ответ: V=180 \(см^3.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так