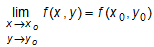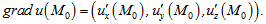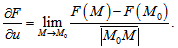Решение примеров с областью определения функции двух переменных

Функции нескольких переменных: основные определения

Обозначением функции пары переменных является следующее соотношение:

z = f(x, y)

Здесь f играет роль символа соответствия.

Геометрический смысл области определения D заключается в том, что D представляет собой какой-то участок на плоскости Оху. Эта область ограничена линиями, принадлежащими, либо не принадлежащими ей.

В том случае, когда функция записана в виде некой формулы без четкого указания на D, имеется в виду, что D включает в себя множество любых значений для переменных, при которых данная формула рассматриваемой функции обладает смыслом.

С целью дальнейшего рассмотрения темы введем некоторые обозначения:

Записи функций пары переменных имеют следующий вид: \(z\left( {x,y} \right), f\left( {x,y} \right), g\left( {x,y} \right), h\left( {x,y} \right), F\left( {x,y} \right)\).

Аргументы обозначают в этом случае таким образом: x, y, t

Малые приращения переменных x, y, z, соответствуют таким значениям: \(\Delta x, \Delta y, \Delta z\).

Обозначение определителя: D

Заметим, что определение для функции одной переменной можно достаточно просто распространить на случаи, когда имеется два или более аргумента. Если рассматривается функция пары переменных, то предполагается множество пар (x, y), которые упорядочены, а их числовые значения взяты из множеств \(x \in X, y \in Y\).

При наличии закономерности, предусматривающей лишь одно значение z в виде числа для каждой пары (х, у), можно заключить, что задана функция двух переменных. Обозначением подобной функции является следующие примеры выражений:

\(z = z\left( {x,y} \right), z = f\left( {x,y} \right), z = F\left( {x,y} \right)\) и другие.

Аналогично можно определить функцию n переменных.

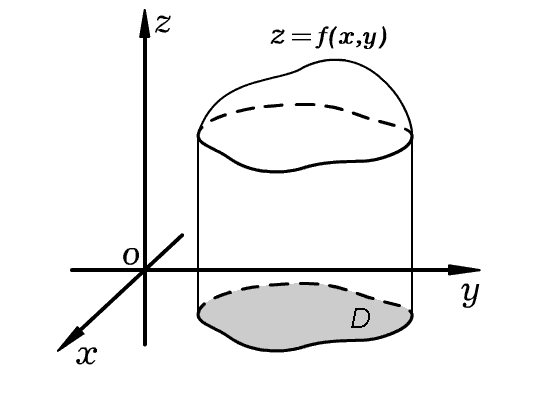
Если имеется некая функция z = f(x, y), то для любых пар (х, у) имеется возможность изобразить точку с определенными координатами, к примеру, М (х, у, z). При этом z = f(x, y). Множество рассматриваемых точек носит название графика функции z = f(x, y). В большинстве случаев график имеет вид определенной поверхности.

На графике область определения представляет собой плоскость ХОУ полностью, либо частично. Например, дана функция:

\(z = - \frac{A}{C}x - \frac{B}{C}y - \frac{D}{C}\)

В данном случае, область определения этой функции соответствует всей координатной плоскости ХОУ. Это объясняется существованием значения z для любой из точек (х, у).

Подобный случай не является единственным. Бывают и другие варианты. Введем понятие области определения.

Рассмотрим характеристики такой функции. Разберем понятия ее предела и непрерывности.

Рассмотрим пример функции:

\(z = \frac{1}{2x^{2} + y^{2}}\)

Заметим, что данная функция не прерывается в какой-либо точке на плоскости. Исключением в этом случае является начало координат, где можно наблюдать бесконечный разрыв функции.

При рассмотрении функций более одной переменной следует познакомиться с понятием частной производной.

В качестве примера рассмотрим функцию пары переменных:

\(z = f\left( {x,y} \right)\)

В этом случае можно найти частные производные по переменной х и по переменной у, которые следует обозначить таким образом:

\(\large\frac{{\partial z}}{{\partial x}}\normalsize = \large\frac{{\partial f}}{{\partial x}}\normalsize = {z'_x} = {f'_x},\;\;\large\frac{{\partial z}}{{\partial y}}\normalsize = \large\frac{{\partial f}}{{\partial y}}\normalsize = {z'_y} = {f'_y}\)

Частные производные второго порядка определяют следующим способом:

\(\large\frac{\partial }{{\partial x}}\normalsize\left( {\large\frac{{\partial f}}{{\partial x}}}\normalsize \right) = \large\frac{{{\partial ^2}f}}{{\partial {x^2}}}\normalsize = {f''_{xx}},\;\; \large\frac{\partial }{{\partial y}}\normalsize\left( {\large\frac{{\partial f}}{{\partial y}}}\normalsize \right) = \large\frac{{{\partial ^2}f}}{{\partial {y^2}}}\normalsize = {f''_{yy}},\)

\(\large\frac{\partial }{{\partial y}}\normalsize\left( {\large\frac{{\partial f}}{{\partial x}}}\normalsize \right) = \large\frac{{{\partial ^2}f}}{{\partial y\,\partial x}}\normalsize = {f''_{xy}},\;\; \large\frac{\partial }{{\partial x}}\normalsize\left( {\large\frac{{\partial f}}{{\partial y}}}\normalsize \right) = \large\frac{{{\partial ^2}f}}{{\partial x\,\partial y}}\normalsize = {f''_{yx}}.\)

В том случае, когда смешанные частные производные представляют собой непрерывные функции, отсутствует зависимость между этими производными и порядком дифференцирования:

\(\large\frac{{{\partial ^2}f}}{{\partial y\,\partial x}}\normalsize = \large\frac{{{\partial ^2}f}}{{\partial x \,\partial y}}\normalsize\)

Существуют правила, согласно которым дифференцируют сложную функцию пары переменных. Представим, что выполняется следующее условие:

\(f\left( {x,y} \right) = g\left( {h\left( {x,y} \right)} \right)\)

Здесь g определена, как функция одной переменной h.

Тогда частные производные соответствуют:

\(\large\frac{{\partial f}}{{\partial x}}\normalsize = g'\left( {h\left( {x,y} \right)} \right)\large\frac{{\partial h}}{{\partial x}}\normalsize,\;\;\large\frac{{\partial f}}{{\partial y}}\normalsize = g'\left( {h\left( {x,y} \right)} \right)\large\frac{{\partial h}}{{\partial y}}\normalsize.\)

Предположим, что выполняется следующее условие:

\(h\left( t \right) = f\left( {x\left( t \right),y\left( t \right)} \right)\)

В таком случае, вычисление производной выполняют, согласно формуле:

\(h'\left( t \right) = \large\frac{{\partial f}}{{\partial x}}\frac{{dx}}{{dt}}\normalsize + \large\frac{{\partial f}}{{\partial y}}\frac{{dy}}{{dt}}\normalsize.\)

В другом случае:

\(z = f\left( {x\left( {u,v} \right),y\left( {u,v} \right)} \right)\)

В результате для определения частных производных целесообразно использовать следующие соотношения:

\(\large\frac{{\partial z}}{{\partial u}}\normalsize = \large\frac{{\partial f}}{{\partial x}}\frac{{\partial x}}{{\partial u}}\normalsize + \large\frac{{\partial f}}{{\partial y}}\frac{{\partial y}}{{\partial u}}\normalsize,\;\;\large\frac{{\partial z}}{{\partial v}}\normalsize = \large\frac{{\partial f}}{{\partial x}}\frac{{\partial x}}{{\partial v}}\normalsize + \large\frac{{\partial f}}{{\partial y}}\frac{{\partial y}}{{\partial v}}\normalsize.\)

Малые приращения функции находят по формуле:

\(\Delta z \approx \large\frac{{\partial f}}{{\partial x}}\normalsize\Delta x + \large\frac{{\partial f}}{{\partial y}}\normalsize\Delta y\)

Определение 8

Градиент функции u (x, y,...) представляет собой вектор с координатами в виде частных производных функции u по x, y,...

Градиент обозначают таким образом:

\(grad u\).

В том случае, когда u является функцией пары переменных:

\(grad u = (u'x, u'y)\)

В том случае, когда u является функцией трех переменных:

\(grad u = (u'_{x}, u'_{y}, u'_{z})\)

Существует способ определения градиента для какой-то точки \(M_{0}\). Для этого требуется подставить координаты рассматриваемой точки в следующее выражение:

Представим, что функция \(F(x, y, z)\) возрастает, двигаясь от точки \(M_{0}\) к некой точке М. Таким образом, функция растет в соответствии с направлением вектора \(\overline{M_{0}М}\). Существует характеристика для описания скорости этого роста.

Рассмотрим варианты поведения функции F в направлении вектора \(\overline{u}\) на графике:

• функция является возрастающей, если \(\frac{dF}{du}>0\);
• функция является убывающей, если \(\frac{dF}{du}<0\);
• функция остается неизменной, если \(\frac{dF}{du}=0\).

С целью определения производной \(\frac{dF}{du}\) следует упростить вычисления и использовать при расчетах скалярное произведение:

Экстремум функции нескольких переменных

Функция \(f\left( {x,y} \right)\) обладает неким локальным максимумом в точке с координатами \(\left( {{x_0},{y_0}} \right)\) в том случае, когда \(f\left( {x,y} \right) < f\left( {{x_0},{y_0}} \right)\) для всех \(\left( {x,y} \right)\), которые необходимо близки к \(\left( {{x_0},{y_0}} \right)\).

Функция \(f\left( {x,y} \right)\) обладает неким локальным минимумом в точке с координатами \(\left( {{x_0},{y_0}} \right)\) в том случае, когда \(f\left( {x,y} \right) > f\left( {{x_0},{y_0}} \right)\) для всех \(\left( {x,y} \right)\), которые необходимо близки к \(\left( {{x_0},{y_0}} \right)\).

Определить стационарные точки в случае функции пары переменных можно с помощью такой системы уравнений:

\(\large\frac{{\partial f}}{{\partial x}}\normalsize = \large\frac{{\partial f}}{{\partial y}}\normalsize = 0\).

Заметим, что по определению локальный максимум и локальный минимум являются стационарными точками функции. Данные точки совместно с точками, принадлежащими области определения функции, в которых отсутствуют частные производные функции, формируют некое множество критических точек этой функции.

Предположим, что имеется некая точка \(\left( {{x_0},{y_0}} \right)\), в которой частные производные первого порядка принимают нулевые значения. Тогда заданная точка является стационарной точкой. Запишем выражение для определителя, в состав которого включены значения частных производных второго порядка, соответствующие данной точке:

\(D = \left| {\begin{array}{*{20}{c}} {\large\frac{{{\partial ^2}f}}{{\partial {x^2}}}\normalsize\left( {{x_0},{y_0}} \right)} & {\large\frac{{{\partial ^2}f}}{{\partial y\,\partial x}}\normalsize\left( {{x_0},{y_0}} \right)}\\ {\large\frac{{{\partial ^2}f}}{{\partial x\,\partial y}}\normalsize\left( {{x_0},{y_0}} \right)} & {\large\frac{{{\partial ^2}f}}{{\partial {y^2}}}\normalsize\left( {{x_0},{y_0}} \right)} \end{array}} \right|.\)

Рассмотрим возможные варианты:

1. Когда D > 0 и частная производная \(\large\frac{{{\partial ^2}f}}{{\partial {x^2}}}\normalsize\left( {{x_0},{y_0}} \right) > 0\), имеем, что \(\left( {{x_0},{y_0}} \right)\) определяется, как локальный минимум.
2. При D > 0 и частной производной \(\large\frac{{{\partial ^2}f}}{{\partial {x^2}}}\normalsize\left( {{x_0},{y_0}} \right) < 0\) имеем, что \(\left( {{x_0},{y_0}} \right)\) определяется, как локальный максимум.
3. Если D < 0, тогда \(\left( {{x_0},{y_0}} \right)\) представляет собой седловую точку.
4. Если D обладает нулевым значением, то для идентификации вида стационарной точки требуется провести дополнительные исследования.

Уравнение касательной плоскости к поверхности \(z = f\left( {x,y} \right)\) в некой точке с координатами \(\left( {{x_0},{y_0},{z_0}} \right)\) можно записать таким образом:

\(z - {z_0} = \large\frac{{\partial f}}{{\partial x}}\normalsize\left( {{x_0},{y_0}} \right)\left( {x - {x_0}} \right) + \large\frac{{\partial f}}{{\partial y}}\normalsize\left( {{x_0},{y_0}} \right)\left( {y - {y_0}} \right).\)

Уравнение нормали к поверхности \(z = f\left( {x,y} \right)\) в некой точке с координатами \(\left( {{x_0},{y_0},{z_0}} \right)\) можно записать следующим образом:

\(\large\frac{{x - {x_0}}}{{\frac{{\partial f}}{{\partial x}}\left( {{x_0},{y_0}} \right)}}\normalsize = \large\frac{{y - {y_0}}}{{\frac{{\partial f}}{{\partial y}}\left( {{x_0},{y_0}} \right)}}\normalsize = \large\frac{{z - {z_0}}}{{ - 1}}\normalsize.\)

Как найти область определения функции многих переменных — подробная инструкция

При записи функции нескольких переменных (например, двух переменных) в виде формулы \(z = f(x, y)\), область определения этой функции является множеством всех значений точек плоскости ХОУ, при которых эта формула имеет смысл, и функция принимает действительные значения.

В действительности, принципы нахождения области определения функции нескольких переменных схожи с правилами для области определения функции одной переменной, которые соответствуют следующему алгоритму действий:

• определение типа или типов ограничений;
• запись и поиск корней соответствующих неравенств;
• запись интервала или интервалов допустимых значений аргумента.

Разница заключается в том, что в случае функции двух переменных область определения представляет собой какое-то множество точек плоскости, а не прямой, как для функции одной переменной.

Если рассматривается функция трех переменных, то областью определения станет множество точек, принадлежащих трехмерному пространству.

Когда речь идет о функции n переменных, область определения соответствует множеству точек абстрактного n-мерного пространства.

Область определения функции двух переменных с корнем n-й степени

Представим некую функцию:

\(z=\sqrt[n]{\phi(x,y)}\)

Здесь n является каким-то натуральным числом. Запишем варианты для области определения функции при разных значениях n:

1. При n в виде четного числа область определения функции соответствует множеству точек плоскости со всеми значениями подкоренного выражения, которые больше или равны нулю. Таким образом: \(\phi(x,y) \geq 0\).
2. При n в виде нечетного числа область определения функции представляет собой множество каких-либо значений  \(\phi(x,y)\), то есть соответствует всей плоскости ХОУ.

Область определения степенной функции двух переменных, если показатель степени является целым числом

Когда функция имеет вид \(z = (\phi(x,y))^{a}\), она определяется таким образом:

• при положительных значениях a область определения соответствует всей плоскости ХОУ, включая оси;
• при отрицательных значениях а область определения функции соответствует множеству значений \(\phi(x,y)\), которые не равны нулю.

Область определения степенной функции двух переменных, если показатель степени является дробным числом

Когда функция имеет вид \(z = (\phi(x,y))^{ \frac{a}{b}}\), она определяется таким образом:

• при положительных значениях \(\frac{a}{b}\) область определения соответствует множеству таких точек на плоскости, в которых \(\phi(x,y) \geq 0\);
• при отрицательных значениях \(\frac{a}{b}\) область определения функции соответствует множеству точек на плоскости, в которых \(\phi(x,y)> 0\).

Область определения логарифмической функции двух переменных

Рассмотрим логарифмическую функцию двух переменных, записанную в виде:

\(z = \log_{a}{\phi(x,y)}\)

Данная функция определена в том случае, когда ее аргумент обладает положительным значением. Тогда областью определения функции является множество таких точек, в которых:

\(\phi(x,y)> 0.\)

Область определения тригонометрических функций двух переменных

Рассмотрим варианты тригонометрических функций и их области определения:

• для функции \(z = sin \phi(x,y)\) областью определения является полностью плоскость ХОУ;
• для функции \(z = cos \phi(x,y)\) областью определения является полностью плоскость ХОУ;
• для функции \(z = tg \phi(x,y)\) областью определения является полностью плоскость ХОУ, за исключением пар чисел, когда \(\phi(x,y)\) обладает значениями \(\frac{\pi}{2}+\pi k,\) где \(k\in Z\);
• для функции \(z =c tg \phi(x,y)\) областью определения является полностью плоскость ХОУ, за исключением пар чисел, когда \(\phi(x,y)\) обладает значениями k, где \(k\in Z.\)

Область определения обратных тригонометрических функций двух переменных

Рассмотрим варианты обратных тригонометрических функций и их области определения:

• для функции \(z = arcsin \phi(x,y)\) областью определения является множество таких точек, при которых \(-1\leq \phi(x,y) \leq 1\);
• для функции \(z = arccos \phi(x,y)\) областью определения является множество таких точек, при которых \(-1\leq \phi(x,y) \leq 1\);
• для функции \(z = arctg \phi(x,y)\) областью определения является полностью плоскость ХОУ;
• для функции \(z =arcc tg \phi(x,y)\) областью определения является полностью плоскость ХОУ.

Область определения дроби как функции двух переменных

Представим, что функция записана следующим образом:

\(z = \frac{a}{\phi(x,y)}\)

В таком случае, область определения данной функции соответствует всем точкам плоскости при выполнении условия:

\(\phi(x,y) \neq 0.\)

Область определения линейной функции двух переменных

Предположим, что функция задана таким образом:

\(z = ax + by + c\)

В этом случае, область определения рассматриваемой функции соответствует полностью всей плоскости ХОУ.

Примеры решения задач