Основные сведения об области определения логарифмической функции
Логарифм числа и его свойства
Логарифм некого числа b по основанию а является показателем степени, в которую требуется возвести основание а для получения в результате числа b.
В качестве обозначения логарифма используют: \(\log _{a}b\)
Данную запись можно прочитать, как «логарифм b по основанию а».
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Рассмотрим следующее равенство:
\(x=\log _{a}b\)
Согласно записанному ранее определению логарифма, получим, что данное соотношение является равносильным следующему:
\(a^{x}=b\)
Рассмотрим пример логарифмического уравнения:
\(\log _{2}8=3\)
Равенство является справедливым по той причине, что:
\(2^{3}=8\)
Логарифмирование — операция по определению логарифма.
В определении логарифма принято использовать числа а и b из множества вещественных чисел. В некоторых случаях применима теория комплексных логарифмов.
С помощью логарифмов удается значительно упростить решение многих задач. Например, в процессе перехода к логарифмическому уравнению умножение может быть заменено на операцию сложения, а вместо деления используют вычитания, также возведение в степень и извлечение корня трансформируются в умножение и деление на показатель степени соответственно.
Математик из Шотландии Джон Непер в 1614 году первым сформулировал определение логарифмов и представил таблицу со значениями тригонометрических функций. Со временем таблицы были уточнены и дополнены. До появления калькуляторов и компьютерной техники эти таблицы активно применялись на протяжении веков для выполнения расчетов в математике, инженерии и других научных областях знаний.
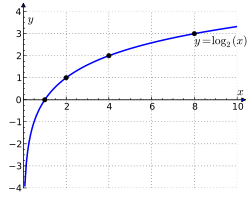
Изобразим в качестве примера двоичный логарифм на графике:
Рассмотрим логарифм какого-то числа из множества вещественных:
\(x=\log _{a}b\)
Исходя из определения логарифма, данное соотношение представляет собой решение следующего уравнения:
\(a^{x}=b\)
В том случае, когда a=1 при \(b\neq 1\), у записанного уравнения отсутствуют решения. Если b=1, то в качестве решения можно представить любое число. Эти два варианта приводят к неопределенности логарифма. Таким же образом, можно сделать вывод об отсутствии логарифма, когда а принимает нулевое или отрицательное значение.
Зная, что показательная функция \(a^{x}\) во всех случаях положительна, исключим также случаи, при которых b имеет отрицательное значение. Обобщая вышесказанное, запишем: вещественный логарифм \(\log _{a}b\) обладает смыслом, если \(a>0,a\neq 1,b>0.\)
Распространенными являются следующими виды логарифмов:
- Натуральные: \(\log _{e}\,b\) или \(\ln \,b\) с основанием в виде числа Эйлера (e).
- Десятичные: \(\log _{10}\,b\) или \(\lg \,b \) с основанием в виде числа 10.
- Двоичные: \(\log_{2}\,b\) или \(\operatorname {lb}\,b\) с основанием 2, которые нашли применение в теории информации, информатике, в разных разделах дискретной математики.
Свойства логарифма удобно использовать при решении различных задач. Рассмотрим главное логарифмическое тождество.
Основным логарифмическим тождеством называют справедливое равенство, которое вытекает из определения логарифма и имеет следующий вид: \( a^{\log _{a}b}=b\)
Согласно равенству пары вещественных логарифмов, логарифмируемые выражения равны, то есть при \(\log _{a}b=\log _{a}\) c справедливо, что \(a^{\log _{a}b}=a^{\log _{a}c},\) тогда по основному логарифмическому тождеству получаем: b=c.
Исходя из определения логарифма, можно вывести следующие справедливые равенства:
\(\log _{a}1=0\)
\(\log _{a}a=1.\)
Рассмотрим, как вычисляют логарифм произведения, частного от деления, степени и корня при положительных значениях переменных.
Произведение:
\(\log _{a}(xy)=\log _{a}(x)+\log _{a}(y)\)
К примеру:
\(\log _{3}(243)=\log _{3}(9\cdot 27)=\log _{3}(9)+\log _{3}(27)=2+3=5\)
Частное от деления:
\(\log _{a}\!\left({\frac {x}{y}}\right)=\log _{a}(x)-\log _{a}(y)\)
Например:
\(\lg \left({\frac {1}{1000}}\right)=\lg(1)-\lg(1000)=0-3=-3\)
Степень:
\(\log _{a}(x^{p})=p\log _{a}(x)\)
Докажем это равенство:
\(\log _{a}{x^{p}}=y\)
\(a^{y}=x^{p}{\displaystyle }a^{y}=x^{p}\)
\(a^{\frac {y}{p}}=x{\displaystyle }a^{\frac {y}{p}}=x\)
\(log_{a}{x}={\frac {y}{p}}{\displaystyle} log_{a}{x}={\frac {y}{p}}\)
\(p\cdot log_{a}{x}=y{\displaystyle} p\cdot log_{a}{x}=y\)
Применим данную формулу для решения примера:
\(\log _{2}(64)=\log _{2}(2^{6})=6\log _{2}(2)=6\)
Степень в основании:
\(\log _{(a^{p})}(x)={\frac {1}{p}}\log _{a}(x)={\frac {\log _{a}(x)}{p}}\)
Докажем, что записанное равенство является справедливым:
\(\log _{a^{p}}{x}=y\)
\(a^{y\cdot p}=x{\displaystyle} a^{y\cdot p}=x\)
\(log_{a}{x}=p\cdot y{\displaystyle} log_{a}{x}=p\cdot y\)
\(\frac {log_{a}{x}}{p}=y\)
В качестве примера упростим выражение:
\(\log _{2^{10}}{\sin {\left({\frac {\pi }{6}}\right)}}={\frac {\log _{2}{\frac {1}{2}}}{10}}=-{\frac {1}{10}}=-0{,}1\)
Корень:
\(\log _{a}{\sqrt[{p}]{x}}={\frac {1}{p}}\)
Докажем данное свойство:
\(\log _{a}{\sqrt[{p}]{x}}=y\)
\(a^{y}={\sqrt[{p}]{x}}{\displaystyle} a^{y}={\sqrt[{p}]{x}}\)
\(a^{p\cdot y}=x{\displaystyle} a^{p\cdot y}=x\)
\(log_{a}{x}=p\cdot y{\displaystyle} log_{a}{x}=p\cdot y\)
\({\frac {log_{a}{x}}{p}}=y{\displaystyle} {\frac {log_{a}{x}}{p}}=y\)
Рассмотрим наглядный пример:
\(\lg {\sqrt {1000}}={\frac {1}{2}}\lg 1000={\frac {3}{2}}=1{,}5\)
Корень в основании:
\(\log _{\sqrt[{p}]{a}}(x)=p\log _{a}(x)\)
Представим доказательства:
\(\log _{\sqrt[{p}]{a}}{x}=y\)
\(a^{\frac {y}{p}}=x{\displaystyle} a^{\frac {y}{p}}=x\)
\(a^{y}=x^{p}{\displaystyle} a^{y}=x^{p}\)
\(a^{\frac {y}{p}}=x{\displaystyle} a^{\frac {y}{p}}=x\)
\(log_{a}{x}={\frac {y}{p}}{\displaystyle} log_{a}{x}={\frac {y}{p}}\)
\(p\cdot log_{a}{x}=y{\displaystyle} p\cdot log_{a}{x}=y\)
Применим записанное свойство на практике:
\(\log _{\sqrt {\pi }}{(4\cdot \operatorname {arctg} {1})}=2\cdot \log _{\pi }{\left(4\cdot {\frac {\pi }{4}}\right)}=2\cdot \log _{\pi }{(\pi )}=2\)
В том случае, когда переменная обладает отрицательным значением, следует обратиться к обобщенной записи перечисленных свойств логарифма:
\(\log _{a}|xy|=\log _{a}|x|+\log _{a}|y|\)
\(\log _{a}\!\left|{\frac {x}{y}}\right|=\log _{a}|x|-\log _{a}|y|\)
Формулы для вычисления произведения допустимо обобщить с расчетом на любое число сомножителей:
\(\log _{a}(x_{1}x_{2}\dots x_{n})=\log _{a}(x_{1})+\log _{a}(x_{2})+\dots +\log _{a}(x_{n})\)
\(\log _{a}|x_{1}x_{2}\dots x_{n}|=\log _{a}|x_{1}|+\log _{a}|x_{2}|+\dots +\log _{a}|x_{n}|\)
Многозначные числа x, y можно умножать с помощью таблиц логарифмов таким образом:
- определить по таблице логарифмы x, y;
- суммировать полученные логарифмы, что соответствует (исходя из первого свойства логарифма) логарифму произведения x\cdot y;
- согласно логарифму произведения определить по таблице значение самого произведения.
Аналогичным способом выполняют деление. Только при этом вместо умножения применяют операцию вычитания, а алгоритм действий остается прежним.
Логарифм \(\log _{a}b\) по основанию a допустимо записать в виде логарифма по другому основанию c:
\(\log _{a}b={\frac {\log _{c}b}{\log _{c}a}}\)
Следствием из данной формулы, если b=c, является перестановка местами основания и логарифмируемого выражения:
\(\log _{a}b={\frac {1}{\log _{b}a}}\)
Обратим внимание на то, что коэффициент \({\frac {1}{\log _{c}a}}=\log _{a}c\) в рассматриваемом выражении замены основания носит названием модуля перехода от одного основания к другому.
При решении логарифмических неравенств следует помнить, что логарифм \(\log _{a}{b}\) обладает положительным значение в том случае, когда a, b расположены с одной стороны относительно единицы, то есть оба больше, либо меньше по сравнению с 1. В противном случае логарифм имеет знак минуса.
Какое-либо неравенство в случае положительных чисел допустимо логарифмировать:
- при основании больше, чем единица, знак неравенства остается без изменений;
- при основании меньше, чем единица, знак неравенство нужно поменять на противоположный.
Существует тождество, которое поможет упростить действия, когда в основании или логарифмируемом выражении содержится степень:
\({\log _{a^{q}}{b}}^{p}={\frac {p}{q}}\log _{a}{b}\)
Данное соотношение получают путем замены в левой части логарифма основания \(a^{q}\) на a по ранее рассмотренной формуле замены основания. Из этого справедливого равенства можно вывести следующее:
\(\log _{a^{k}}b={\frac {1}{k}}\log _{a}b;\quad \log _{\sqrt[{n}]{a}}b=n\log _{a}b;\quad \log _{a^{k}}b^{k}=\log _{a}b\)
Другим полезным тождеством является:
\(c^{\log _{a}b}=b^{\log _{a}c}\)
В этом случае, можно заметить совпадение логарифмов слева и справа по основанию а, то есть являются равными \(\log _{a}b\cdot \log _{a}c\). По следствию из главного логарифмического тождества получим, что части слева и справа равны друг другу тождественно.
С помощью логарифмирования предыдущего тождества по какому-либо произвольно выбранному основанию d можно получить дополнительное тождество для замены оснований:
\(\log _{a}b\cdot \log _{d}c=\log _{d}b\cdot \log _{a}c.\)
Логарифмическая функция, ее свойства и график
При рассмотрении какого-либо логарифмируемого числа в качестве переменной получается логарифмическая функция, имеющая следующий вид: \(y=\log _{a}x\).
Областью определения данной функции являются такие значения, которые соответствуют интервалу:
\(a>0;\ a\neq 1;x>0.\)
Область значений логарифмической функции определена таким образом:
\(E(y) = (-\infty ;+\infty).\)
На графике логарифмическая функция имеет вид кривой, которую часто называют логарифмикой. Согласно формуле, с помощью которой осуществляют замену основания логарифма, сделаем вывод о том, что:
- графики логарифмических функций, имеющих разные основания, больше единицы, различаются по масштабу относительно оси y;
- графики логарифмических функций для оснований, меньших, чем единица, представляют собой их зеркальное отражение по отношению к горизонтальной оси.
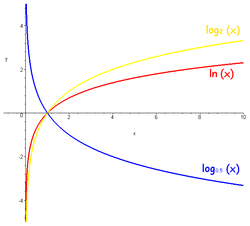
Изобразим графики логарифмических функций:
Согласно определению, логарифмическая функция является обратной для показательной функции \(y=a^{x}\). По этой причине графические изображения данных функций будут симметричными по отношению к биссектрисе первого и третьего квадрантов. Обе эти функции трансцендентны.
Заметим следующие особенности логарифмической функции:
- строгое возрастание графика, если a>1;
- строгое убывание графика, если 0<a<1.
Графически изображенная логарифмическая функция в любом случае будет пересекать точку с координатами (1;0). Функция не прерывается и дифференцируется без ограничений на любом участке в рамках собственной области определений.
Ось ординат при x=0 представляет собой вертикальную асимптоту, так как:
- \(\lim _{x\to 0+0}\log _{a}x=-\infty\) при a>1;
- \(\lim _{x\to 0+0}\log _{a}x=+\infty\) при 0<a<1.
Производную логарифмической функции вычисляют по формуле:
\({\frac {d}{dx}}\log _{a}x={\frac {1}{x\cdot \ln a}}\)
Логарифмическая функция представляет собой непрерывное решение, которое считают единственно верным, для следующего функционального уравнения:
\(f(xy)=f(x)+f(y).\)
Свойства функции \(y={{log}_a x\ }\), при a >1:
- Областью определения данной функции является интервал \((0,+\infty )\).
- Значения функции определяются, как множество действительных чисел.
- Данную функцию нельзя отнести к типу четных или нечетных.
- График пересекает оси координат. С осью Oy точки пересечения отсутствуют. Если \(y=0\), \({{log}_a x\ }=0,\ x=1\). Функция пересекается с осью Ox в точке (1,0).
- Функция является положительной, если \(x\in (1,+\infty )\). Функция является отрицательной в том случае, когда \(x\in (0,1)\).
- \(y'=\frac{1}{xlna}\).
- Точки минимума и максимума: \(\frac{1}{xlna}=0\), при этом корни отсутствуют, то есть максимальные и минимальные точки также отсутствуют.
- Функция является возрастающей на всей области определения.
- \(y^{''}=-\frac{1}{x^2lna}\).
- Промежутки выпуклости и вогнутости: \(-\frac{1}{x^2lna}\). Функция является выпуклой на всей области, в которой определяется.
- \({\mathop{lim}_{x\to 0} y\ }=-\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=+\infty.\)
Рассмотрим свойства функции \(y={{log}_a x\ }, 0 < a < 1:\)
- Функция определяется на интервале \((0,+\infty).\)
- Значениями функции являются все числа из множества действительных.
- Данную функцию нельзя отнести к типу четных или нечетных.
- Отсутствуют пересечения графика с осью Oy. Если \(y=0, {{log}_a x\ }=0,\ x=1\).Функция пересекает ось Ox в точке с координатами: (1,0).
- Функция является положительной, если \(x\in (0,1)\). Функция является отрицательной в том случае, когда \(x\in (1,+\infty).\)
- \(y'=\frac{1}{xlna}.\)
- Точки минимума и максимума: \( \frac{1}{xlna}=0\); в этом случае корни отсутствуют — значит, отсутствуют максимальные и минимальные точки.
- Функция является убывающей на всей области, в которой она определена.
- \(y^{''}=-\frac{1}{x^2lna}\).
- Промежутки выпуклости и вогнутости: \( -\frac{1}{x^2lna}>0\). Функция является вогнутой на всей области, в которой она определена.
- \(\mathop{lim}_{x\to 0} y\ =+\infty ,\ {\mathop{lim}_{x\to +\infty } y\ }=-\infty\).
Область определения функции с корнем
По определению, логарифмическая функция имеет вид:
\(y=\log _{a} x,\; a,\, x>0,\; a\ne 1.\)
Областью определения функции \(D\left(y\right)\) является такое множество, на котором задана функция \(y=f\left(x\right)\), при этом каждая точка рассматриваемого множества соответствует определенному значению функции.
В случае логарифмической функции, в том числе, с корнем квадратным, дробью со знаменателем, отличным от нуля, область определения соответствует какому-либо числу со знаком плюс из множества действительных чисел:
\(D\left(\log _{a} x\right):x\in \left(0;\; +\infty \right)\)
Рассмотрим несколько примеров логарифмических функций, чтобы узнать область их определений:
\(y=\log _{ \frac{2}{3} } x;\)
\(y=\log _{ \sqrt{5}} x;\)
\(y=\log _{7} x.\)
Областью определения записанных логарифмических функций, в том числе, с корнем, является интервал \((0, +\infty)\).
Попробуем решить задачу. Здесь требуется искать область определения в случае функции:
\(f(x)=\frac{1}{ln(x+3)}\)
Условия следующие:
х + 3 > 0
\(x + 3 \neq 1\)
Тогда:
х > -3
\(x \neq -2\)
Тогда область определения соответствует следующим значениям:
\(D(f) = (-3, -2) \cup (-2, +\infty).\)
Примеры решения задач
Дана функция:
\(y=\log _{\pi } \left(2x-4\right).\)
Требуется обозначить область определения данной функции.
Решение
Область определения рассматриваемой функции можно задать с помощью следующего неравенства:
\(2x-4>0.\)
Найдем решения для этого линейного неравенства:
\(2x>4\Rightarrow x>2\Rightarrow x\in \left(2;\; +\infty \right).\)
В результате:
\(D\left(y\right):x\in \left(2;\; +\infty \right)\)
Ответ: \(D\left(y\right):x\in \left(2;\; +\infty \right).\)
Имеется некая функция:
\(y=\log _{2} \left(\left(x-1\right)\left(x+5\right)\right).\)
Нужно найти область, на которой определяется данная функция.
Решение
Логарифм определен в том случае, когда подлогарифмическая функция обладает положительным значением. Исходя из этого, запишем:
\(D\left(y\right):\left(x-1\right)\left(x+5\right)>0.\)
Решим получившееся неравенство:
\(\left(x-1\right)\left(x+5\right)>0.\)
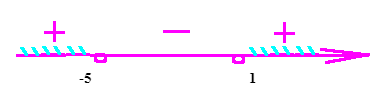
Воспользуемся способом интервалов. В процессе определим, каковы нули всех сомножителей:
\(\begin{array}{c} {x-1=0\Rightarrow x=1,} \\ {x+5=0\Rightarrow x=-5,} \end{array}\)
В результате:
\(D\left(y\right):x\in \left(-\infty ;\; -5\right)\bigcup \left(1;\; +\infty \right).\)
Ответ: \(x\in \left(-\infty ;\; -5\right)\bigcup \left(1;\; +\infty \right).\)
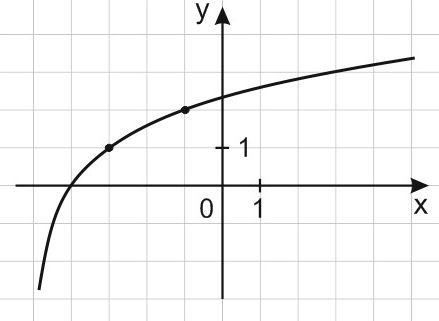
Построен график логарифмической функции \(f\left(x\right)={{log}_a \left(x+b\right)}\):
Требуется определить \(f\left(11\right)\).
Решение
Заметим, что изображенный график функции \(y={{log}_a \left(x+b\right)\ }\) пересекает следующие точки:
(-3; 1)
(-1; 2)
Следует выполнить подстановку данных точек в уравнение функции. Получим:
\(\left\{ \begin{array}{c}{{log}_a \left(-3+b\right)=1\ \ } \\{{log}_a \left(-1+b\right)\ }=2 \end{array}\right.\)
Тогда:
\(\left\{ \begin{array}{c}b-3=a \\b-1=a^2 \end{array};\right.\)
Путем вычитания из второго уравнения первого получим:
\(a^2-a=2; a^2-a-2=0;\)
a=2 или a=-1
Отрицательное значение является посторонним, так как a = 0, исходя из определения основания логарифма.
В результате:
\(b=a+3=5; f\left(x\right)={{log}_2 \left(x+5\right)\ }\)
\(f\left(11\right)={{log}_2 16=4.}\)
Ответ: 4.
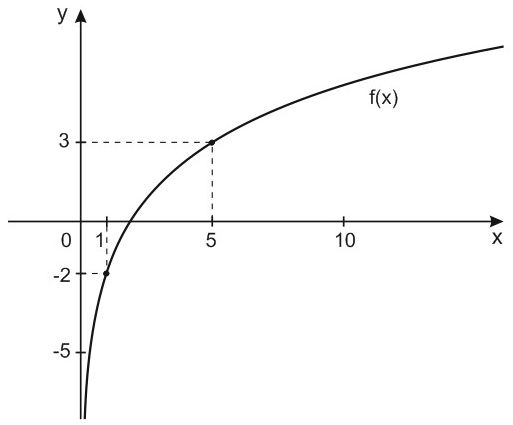
Представлено графическое изображение функции \(f\left(x\right)=a{{log}_5 x }-c:\)
Требуется вычислить \(f(0,2)\).
Решение
Заметим, что функция на графике пересекает следующие точки:
\(\left(1;-2\right)\)
\(\left(5;3\right)\)
Тогда путем поочередной подстановки координат данных точек в уравнение функции получим:
\(\left\{ \begin{array}{c}a{{log}_5 1\ }-c=-2 \\a{{log}_5 5\ }-c=3 \end{array}\right.\)
\(\left\{ \begin{array}{c}-c=-2 \\a-c=3 \end{array}\right.\)
\(\left\{ \begin{array}{c}c=2 \\a=5 \end{array}\right.\)
Уравнение функции:
\(f\left(x\right)=5{{log}_5 x }-2.\)
Определим значение \(f\left(0,2\right)=f\left(\frac{1}{5}\right):\)
\(\displaystyle 5\cdot {{log}_5 \frac{1}{5}\ }-2=-5-2=-7.\)
Ответ: -7.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так