Общая теорема Фалеса о пропорциональных отрезках
Теорема Фалеса — что это такое, история
Теорема Фалеса является частным случаем теоремы о вписанном угле. Как и теорема о вписанном угле, ее определение также основано на диаметре и углах внутри окружности.
Что такое обобщенная теорема Фалеса
Теорема Фалеса гласит, что:
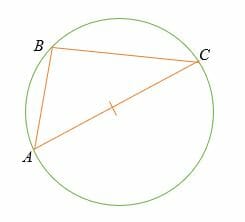
Если три точки A, B и C лежат на окружности, при этом линия AC является диаметром окружности, то угол ∠ABC является прямым углом (90°).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В качестве альтернативы мы можем сформулировать теорему Фалеса как:
Диаметр окружности всегда составляет прямой угол к любой точке окружности.
Вы заметили, что теорема Фалеса является частным случаем теоремы о вписанном угле (центральный угол = удвоенный вписанный угол).
Существует несколько способов доказать теорему Фалеса. Мы можем использовать методы геометрии и алгебры, чтобы доказать эту теорему. Поскольку это тема геометрии, давайте рассмотрим самый простой метод ниже.
Как решить теорему Фалеса
Чтобы доказать теорему Фалеса, нарисуйте перпендикулярную биссектрису ∠
Пусть точка M — средняя точка прямой AC.
Также пусть ∠MBA = ∠BAM = β и ∠MBC =∠BCM =α
Линия AM = MB = MC = радиус окружности.
ΔAMB и ΔMCB являются равнобедренными треугольниками.
По теореме о сумме треугольников:
∠BAC +∠ACB +∠CBA = 180°;
β + β + α + α = 180°.
Учитывайте уравнение:
2 β + 2 α = 180°;
2 (β + α) = 180°.
Разделите обе стороны на 2.
β + α = 90°.
Следовательно, ∠ABC = 90°, доказано.
История
Теорема Фалеса приписывается Фалесу, греческому математику и философу, который жил в Милете. Он первым инициировал и сформулировал теоретическое изучение геометрии, чтобы сделать астрономию более точной наукой.
Фалес был первым известным греческим философом, ученым и математиком. Ему приписывают пять теорем элементарной геометрии.
Миниатюра Фалеса Милетского
Фалес, по-видимому, является первым известным греческим философом, ученым и математиком, хотя по профессии он был инженером. Считается, что он был учителем Анаксимандра (611 г. до н.э. — 545 г. до н.э.) и был первым натурфилософом Милетской школы. Однако ни одно из его сочинений не сохранилось, поэтому трудно определить его взгляды или быть уверенным в его математических открытиях. Действительно, неясно, писал ли он вообще какие-либо работы, а если и писал, то они, безусловно, были утеряны ко времени Аристотеля, который не имел доступа ни к каким трудам Фалеса. С другой стороны, есть утверждения, что он написал книгу по навигации, но они основаны на небольшом количестве доказательств. В книге по навигации предполагается, что он использовал созвездие Малой Медведицы, которое он определил, как важную особенность в своих методах навигации. Даже если книга вымышлена, вполне вероятно, что Фалес действительно определил созвездие Малой Медведицы.
Ссылка на Фалеса была сделана Проклом и Диогеном Лаэртием, документирующим заявление Памфилы о том, что Фалес «был первым, кто вписал в круг прямоугольный треугольник».
Индийские и вавилонские математики знали это для особых случаев еще до того, как Фалес доказал это. Считается, что Фалес узнал, что угол, вписанный в полукруг, является прямым углом во время своих путешествий в Вавилон. Теорема названа в честь Фалеса, потому что древние источники утверждают, что он был первым, кто доказал теорему, используя свои собственные результаты о том, что базовые углы равнобедренного треугольника равны и что сумма углов треугольника равна 180 °.
Теорема о трех перпендикулярах
Теорема о трех перпендикулярах объясняется некоторыми конкретными примерами.
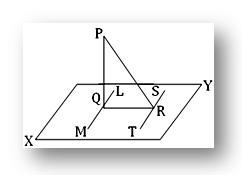
Если PQ перпендикулярен плоскости XY и если от Q, основания перпендикуляра, прямая QR проводится перпендикулярно любой прямой ST в плоскости, то PR также перпендикулярен ST.
Построение: Через Q проведите в плоскости XY прямую линию LM, параллельную ST.
Доказательство: Поскольку LM параллелен ST, а QR перпендикулярен ST, следовательно, QR перпендикулярен LM. Опять же, PQ перпендикулярен плоскости XY; следовательно, он перпендикулярен прямой LM. Следовательно, LM перпендикулярен как PQ, так и QR в точке Q. Это означает, что LM перпендикулярен плоскости PQR. Теперь ST и LM параллельны, а LM перпендикулярен плоскости PQR; следовательно, ST перпендикулярен плоскости PQR. Следовательно, ST перпендикулярен PR или, другими словами, PR перпендикулярен ST.
Прямые линии в пространстве, параллельные данной прямой, параллельны друг другу.
Пусть AB и CD — две прямые, каждая из которых параллельна заданной прямой LM. Мы должны доказать, что прямые AB и CD параллельны друг другу.
Прямые линии в пространстве
Построение: Нарисуйте плоскость PQR, перпендикулярную LM, и давайте предположим, что нарисованная плоскость разрезает LM, AB и CD в точках P, Q и R соответственно.
Доказательство: По гипотезе AB параллельна LM, а по конструкции LM перпендикулярна плоскости PQR. Следовательно, AB также перпендикулярно плоскости PQR. Аналогично, CD также перпендикулярен той же плоскости. Таким образом, каждый из AB и CD перпендикулярен одной и той же плоскости PQR. Следовательно, прямые AB и CD параллельны друг другу.
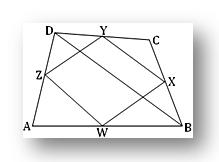
Докажите, что четырехугольник, образованный соединением средних точек смежных сторон косого четырехугольника, является плоскостным параллелограммом. Пусть W, X, Y и Z — средние точки сторон AB, BC, CD и DA косого четырехугольника ABCD. Мы должны доказать, что четырехугольник WXYZ является параллельным параллелограммом.
Конструкция: Соедините WX, XY, YZ, WZ и BD.
Доказательство: Палочка Z — это средние точки сторон AB и AD соответственно в плоскости △ ABD. Следовательно, ZW параллелен BD и ZW = 1/2 BD. Аналогично, X и Y являются средними точками сторон BC и CD соответственно в плоскости △ BCD. Следовательно, XY параллелен BD и XY = 1/2 BD. Поскольку оба ZW и XY параллельны BD, следовательно, они параллельны друг другу. Следовательно, существует плоскость, проходящая через ZW и YX.
Аналогично, WX и ZY параллельны друг другу, и, следовательно, существует плоскость, проходящая через WX и ZY. Обе плоскости, проходящие через ZW и YX, а также через WX и ZY, проходят через четыре точки W, X, Y и Z. Следовательно, очевидно, что эти две плоскости должны быть одинаковыми. Следовательно, четырехугольник WXYZ является копланарным. Опять же, ZW параллелен YX и ZW = YX. Следовательно, четырехугольник WXYZ представляет собой параллелограмм.
Общая формулировка, теорема о пропорциональных отрезках
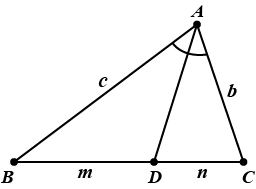
Основная теорема о пропорциональности, также известная как теорема Фалеса, гласит, что «линия, проведенная параллельно одной стороне треугольника и пересекающая две другие стороны, делит две другие стороны в равной пропорции». Например, на данном рисунке линия DE проведена параллельно стороне BC таким образом, что она соединяет две другие стороны, AB и AC. Согласно основной теореме о пропорциональности, можно предположить, что AD/DB = AE/EC.
Основная теорема о пропорциональности
Основная теорема о пропорциональности была впервые сформулирована Фалесом, греческим математиком. Следовательно, она также известна как теорема Фалеса. Фалес первым инициировал и сформулировал Теоретическое изучение геометрии, чтобы сделать астрономию более точной наукой.
Основная теорема о пропорциональности гласит, что если прямая параллельна стороне треугольника, которая пересекает другие стороны в двух различных точках, то линия делит эти стороны пропорционально.
На рисунке рядом, если мы считаем, что DE параллелен BC, то согласно теореме, AD/BD=AE/CE.
Доказательство
Дано: В ΔABC, DE параллелен BC
Линия DE пересекает стороны AB и AC в точках D и E соответственно.
Нужно доказать: AD/BD=AE/CE.
Построение: Нарисуйте EF ⟂ AD и DG⟂ AE и соедините сегменты BE и CD.
Доказательство:
Площадь треугольника= ½ × основание × высота
В ΔADE и ΔBDE,
Ar(ADE)Ar(DB)=12=AD=EF12=DB=EF=ADDB(1);
В ΔADE и ΔCDE,
Ar(ADE)Ar(EC)=12=AE=DG12=EC=DG=AEEC(2).
Обратите внимание, что ΔDBE и ΔECD имеют общее основание DE и лежат между одними и теми же параллелями DE и BC.Кроме того, мы знаем, что треугольники, имеющие одинаковое основание и лежащие между одними и теми же параллелями, равны по площади.
Итак, мы можем сказать, что:
Ar(ΔDBE)=Ar(ΔECD).
Следовательно,
A(ΔADE)A(ΔBDE)=A(ΔADE)A(ΔCDE).
Следовательно,
AD/BD=AE/CE.
В теореме также есть обратное утверждение, которое гласит, что если линия разделяет любые две стороны треугольника в одинаковом соотношении, то линия параллельна третьей стороне.
Свойства теоремы о пропорциональных отрезках
Данная теорема имеет 2 свойства:
- Свойство биссектрисы угла.
- Свойство перехватов, выполненных тремя параллельными линиями на поперечной.
Свойство биссектрисы угла
Утверждение: В треугольнике биссектриса угла делит сторону, противоположную углу, в соотношении остальных сторон.
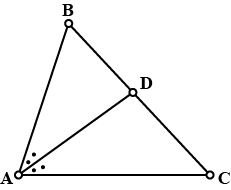
Биссектриса угла
На данном рисунке сегмент AD представляет собой биссектрису угла ∠BAC.
В соответствии с собственностью,
BD/DC=AB/AC.
Свойство перехватов, выполненных тремя параллельными линиями на поперечной
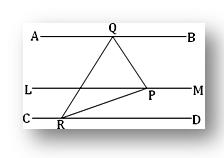
Утверждение: Отношение пересечений, выполненных на поперечной тремя параллельными линиями, равно отношению соответствующих пересечений, выполненных на любой другой поперечной той же параллельной линии.
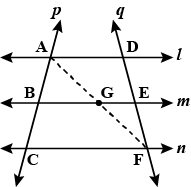
Рассмотрим приведенный выше рисунок, линии l, m и n параллельны друг другу. Поперечные p и q пересекают прямые в точках A, B, C и D, E, F. Таким образом, в соответствии со свойством,
AB/BC=DE/EF.
Доказательство в случае параллельных и не параллельных прямых
Параллельные линии — это две или более прямых, которые лежат в одной плоскости и никогда не пересекаются друг с другом, называются параллельными линиями. Они равноудалены друг от друга и имеют одинаковый наклон.
Стороны различной формы параллельны друг другу. Параллельные линии представлены парой вертикальных линий между названиями линий, например PQ ︳︳XY.
- Мы можем видеть параллельные линии на перекрестке «зебра», линии блокнота и на железнодорожных путях вокруг нас.
- Каждая линия может иметь множество параллельных линий.
- Параллельные линии можно растягивать до бесконечности, не пересекая их ни в одной точке.
Две линии в одном и том же трехмерном пространстве, которые не пересекаются, не обязательно должны быть параллельными. Только если они находятся в общей плоскости, они называются параллельными; в противном случае они называются косыми линиями.
Противоположность параллели — прямая, ортогональная, нормальная или перпендикулярная. Но эти башни не противоположны параллельным, они просто не параллельны.
Поперечная линия — это линия или отрезок линии, который пересекает две или более других линий или отрезков линии. Когда поперечная пересекает параллельные прямые, многие углы совпадают.
Доказательство параллельных прямых
Представьте себе железнодорожное полотно и дорогу, пересекающую рельсы. Вы знаете, что железнодорожные пути параллельны; в противном случае поезд не смог бы проехать по ним, не опрокинувшись. Но как доказать, что они параллельны? Во-первых, нужно вспомнить определение параллельных линий, означающее, что они представляют собой пару линий, которые никогда не пересекаются и всегда находятся на одинаковом расстоянии друг от друга. Затем взять в расчет поперечную линию, которая пересекает две другие линии. На этом этапе соединяем железнодорожные пути с параллельными линиями, а дорогу — с поперечными.
Теперь посмотрим на углы, образованные поперечными параллельными линиями. Когда дело доходит до доказательства параллельности двух прямых, все, на что вам нужно смотреть, — это углы. В частности, мы должны искать пары:
- Соответственные углы.
- Альтернативные внутренние углы.
- Альтернативные внешние углы, или дополнительные углы.
Если мы найдем только одну пару, то мы знаем, что линии параллельны. Кроме того, мы увидим, что каждая пара имеет один угол на одном пересечении и другой угол на другом пересечении. Имеется в виду точка, где поперечная пересекает одну из параллельных прямых. Поскольку в паре параллельных прямых есть две прямые, то есть два пересечения.
Соответствующие углы
Соответственные углы — это углы, которые находятся под одним и тем же углом на каждом пересечении.
Это означает, что если мой первый угол находится в верхнем левом углу одного пересечения, то соответствующий угол на другом пересечении также находится в верхнем левом углу. Если соответственные углы имеют одинаковое измерение, то линии параллельны. Мы можем сопоставить углы в верхнем левом, верхнем правом, нижнем левом или нижнем правом углу.
То, что мы здесь ищем, заключается в том, совпадают ли эти два угла или равны друг другу. Если это так, то линии параллельны. Итак, если оба этих угла измерены в 60 градусов, то вы знаете, что линии параллельны. Но, если углы измеряются по-разному, то автоматически эти две линии не параллельны.
Альтернативные внутренние углы
Альтернативные внутренние углы — это углы, которые находятся на противоположных сторонах поперечной и внутри пары параллельных прямых.
Итак, у вас будет один угол на одной стороне поперечной и другой угол на другой стороне поперечной. И оба этих угла будут находиться внутри пары параллельных прямых. Внутренняя часть параллельных линий — это часть между двумя линиями. Итак, для железнодорожных путей внутренняя часть путей — это та часть, которую покрывает поезд, когда он проезжает по рельсам. Если альтернативные внутренние углы равны, то линии параллельны. Мы можем сопоставить верхнее внутреннее левое с нижним внутренним правым или верхнее внутреннее правое с нижним внутренним левым.
Также здесь, если любая из этих пар равна, то линии параллельны. Итак, допустим, верхний внутренний левый угол равен 45°, а нижний внутренний правый также равен 45°, тогда вы можете сказать, что линии параллельны.
Альтернативные внешние углы
Альтернативные внешние углы — это углы, которые находятся на противоположных сторонах поперечной и вне пары параллельных прямых.
Возвращаясь к железнодорожным путям, эти пары углов будут иметь один угол на одной стороне дороги, а другой угол — на другой стороне дороги. Но оба этих угла будут находиться за пределами путей, что означает, что они будут находиться на той части, которую поезд не покрывает, когда он проезжает по путям. Если любой из альтернативных внешних углов равен, линии будут параллельны.
Примеры решения задач, формулы
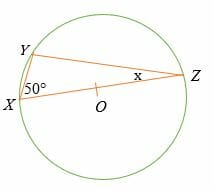
Учитывая, что точка O является центром окружности, показанной ниже, найдите значение x.
Решение:
Учитывая, что прямая XY является диаметром окружности, то по теореме Фалеса:
∠XYZ = 90°.
Сумма внутренних углов треугольника = 180°
90° + 50° + x =180°.
Упростить:
140° + x =180°
Вычесть 140° с обеих сторон:
x = 180° - 140°;
x = 40°.
Итак, значение x равно 40 градусам.
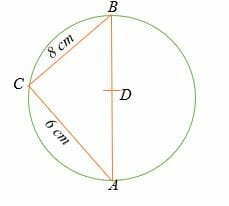
Если точка D является центром окружности, показанной ниже, вычислите диаметр окружности.
Решение:
Согласно теореме Фалеса, треугольник ABC — это прямоугольный треугольник, где ∠ACB = 90°.
Чтобы найти диаметр окружности, примените теорему Пифагора.
CB2 + AC2 =AB2;
82 + 62 = AB2;
64 + 36 = AB2;
100 = AB2;
AB = 10.
Следовательно, диаметр круга составляет 10 см.
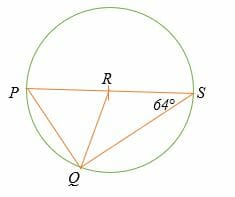
Найдите меру угла PQR в окружности, показанной ниже. Предположим, что точка R является центром окружности.
Решение:
Треугольники RQS и PQR являются равнобедренными треугольниками.
∠RQS =∠RSQ =64°.
По теореме Фалеса, ∠PQS = 90°.
Итак, ∠PQR = 90° - 64° = 26°.
Следовательно, мера угла PQR равна 26°.
Какое из следующих утверждений верно относительно определения теоремы Фалеса?
A. Центральный угол в два раза превышает меру вписанного угла
B. Угол, вписанный в полукруг, будет прямым углом.
C. Диаметр окружности — это самая длинная хорда.
D. Диаметр окружности в два раза больше длины радиуса.
Решение:
Правильный ответ таков:
B. Угол, вписанный в полукруг, будет прямым углом.
В круге, показанном ниже, линия AB — это диаметр круга с центром C.
Найдите меру ∠ BCE.
∠ DCA
∠ АCE
∠ DCB
Решение:
Данный треугольник ACE является равнобедренным треугольником,
∠ CEA =∠ CAE = 33°.
Итак, ∠ ACE=180° – (33° + 33°).
∠ ACE = 114°
Но углы на прямой = 180°.
Следовательно, ∠ BCE = 180° – 114° = 66°.
Треугольник ADC является равнобедренным треугольником, следовательно, ∠ DAC =20°.
По теореме о сумме треугольников, ∠DCA = 180° – (20° + 20°).
∠ DCA = 140°;
∠ DCB = 180° – 140° = 40°.
Какова мера ∠ABC?
Решение:
Теорема Фалеса гласит, что BAC = 90°
И по теореме о сумме треугольников,
∠ABC + 40° + 90° = 180°;
∠ABC = 180° – 130° = 50°.
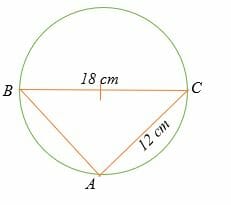
Найдите длину AB в круге, показанном ниже.
Решение:
Треугольник ABC — это прямоугольный треугольник.
Примените теорему Пифагора, чтобы найти длину AB.
AB2 + 122 = 182;
AB2 + 144 = 324;
AB2 = 324 – 144;
AB2 = 180;
AB = 13,4.
Следовательно, длина AB составляет 13,4 см.
В треугольнике ABC сегмент AD является биссектрисой угла ∠BAC. BD = 6, DC = 8, AB =15.
Ответ:
Сегменты AD делят пополам ∠BAC (задано)
.’. AB/AC=BD/DC (свойство биссектрисы угла)
Предположим, что AC= x
.’. 15/x=6/8;
.’. 15 × 8 = 6 × x;
.’. x= (15 × 8) / 6 = 20.
Следовательно, AC = 20.
Нам дано, что в треугольнике PQR MN пересекает PQ и PR в точках M и N соответственно, так что PM = 3 см, MQ = 9 см, PN = 2 см и NR = 6 см. Является ли MN параллельным QR?
Ответ:
PM= 3 см, MQ=9 см
Теперь, PM/MQ=3/9=1/3
Кроме того, PN=2 см, NR=6 см.
Теперь PN/NR= 2/6=1/3.
Следовательно, PM/MQ=PN/NR
Следовательно, в соответствии с обратной основной теоремой о пропорциональности мы имеем MN, параллельный треугольник.
Теорема Фалеса имеет некоторые применения:
- Мы можем точно провести касательную к окружности, используя теорему Фалеса. Для этой цели вы можете использовать заданный квадрат.
- Мы можем точно найти центр окружности, используя теорему Фалеса. Инструменты, используемые для этого приложения, представляют собой набор квадратов и лист бумаги. Во-первых, вы должны поместить угол на окружность — пересечения двух точек с окружностью указывают диаметр. Мы можем повторить это, используя другую пару точек, что даст другой диаметр. Пересечение диаметров даст центр окружности.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так