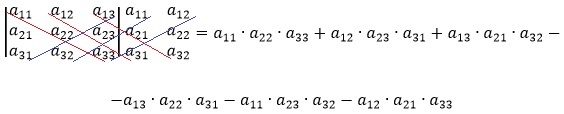Нахождение определителя матрицы 3 порядка

Содержание:

Содержание

Определитель матрицы 3 порядка, описание

Детерминант или определитель матрицы третьего порядка вида \(A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}\) является сопоставляемое с ним число

\(\left|A\right|=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-(a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+a_{11}a_{23}a_{32})\)

Для обозначения данной величины используют символы: |А|, Δ, det A.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Правила для нахождения

Для вычисления детерминанта матрицы 3×3 не нужно заучивать формулу. Данное число можно найти с помощью двух способов:

правила треугольников;
правила Саррюса.

Нахождение методом треугольника

Правило основывается на том, что произведение диагональных составляющих и произведения вершин двух треугольников уменьшаемой матрицы суммируются. Произведение диагональных элементов и произведения вершин треугольников в вычитаемой матрице записываются со знаком минус.

Схематическое изображение рассматриваемого правила выглядит так:

По схеме можно восстановить формулу нахождения определителя матрицы третьего порядка, которая приведена в определении детерминанта:

\(a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{11}a_{23}a_{32}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-(a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+a_{11}a_{23}a_{32})\)

Пример

Найти определитель матрицы:

\(A=\begin{pmatrix}1&3&4\\0&2&1\\1&5&-1\end{pmatrix}\)

Решение

\(\left|A\right|=\begin{vmatrix}21&12&14\\21&12&56\\25&12&14\end{vmatrix}=21\times12\times14+12\times56\times25+14\times12\times21-14\times12\times25-12\times56\times21-21\times12\times14=2016\)

Метод Саррюса

Для нахождения определителя матрицы 3×3 необходимо соблюсти условия в следующей последовательности:

два первых столбца приписать по левую сторону от детерминанта;
произведения компонентов главной диагонали и ей параллельных записать с положительным знаком;
произведения элементов, расположенных на побочной и параллельных ей диагоналях, записать с отрицательным знаком.

Вычисление определителя матрицы по рассматриваемому правилу схематически можно изобразить так:

Пример

Рассчитать по методу Сюрраса детерминант матрицы

\(A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\end{pmatrix}\)

Решение

\(\left|A\right|=\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}\;=\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}\begin{array}{c}1\\4\\7\end{array}\begin{array}{c}2\\5\\8\end{array}=1\times5\times9+2\times6\times7+3\times4\times8-3\times5\times7-1\times6\times8-2\times4\times9=0\)

Свойства определителя

Преобразование столбцов и строк незначительными действиями не оказывает влияния на значение детерминанта.
Перемена строк и столбцов местами влечет за собой изменение значения детерминанта на противоположное.
Детерминант треугольной матрицы можно вычислить путем умножения составляющих, находящихся на главной диагонали.

Насколько полезной была для вас статья?

Рейтинг: 1.80 (Голосов: 5)

Заметили ошибку?

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»