Вычисление определителя матрицы четвертого порядка

Определитель матрицы 4 порядка

Существует разные типы матриц. При рассмотрении данной темы важно уточнить понятия некоторых из них:

• в том случае, когда матрица обладает единственным элементом, она является совпадающей со своим единственным скаляром;
• квадратная матрица представляет собой такую матрицу, которая имеет равное число столбцов и строк.

Алгебраические действия с матрицами характеризуются определенным алгоритмом и порядком. Подобные операции отличаются от манипуляций с простыми числами. Кроме алгебраических действий, над матрицами выполняют и другие операции. К примеру, транспортирование матрицы.

В задачах часто встречаются примеры нахождения определителя матриц разных порядков. Матрицы первого, второго, третьего, четвертого и других порядков относят к квадратным матрицам.

В том случае, когда элементы матрицы имеют вид действительных чисел, то и определитель является действительным числом. Определитель обозначают detA или |A|. Определитель первого порядка соответствует скаляру рассматриваемой матрицы.

Определители второго и третьего порядка определяются в соответствии со стандартным алгоритмом, то есть с помощью известных формул. Для того чтобы вычислить определитель больше третьего порядка, требуется ознакомиться с понятием минора матрицы (М).

Свойства определителя:

• при перестановке местами двух строк или столбцов знак определителя меняется;
• при умножении строки или столбца на число, весь определить также умножится на число;
• в том случае, когда одну строку сколько угодно раз прибавляют или вычитают из другой, определитель не меняется;
• при наличии одинаковых, пропорциональных или заполненных нулями двух строк определителя весь определитель равен нулю;
• все перечисленные свойства справедливы в случае столбцов;
• транспортирование матрицы не сопровождается изменением определителя;
• определитель произведения матриц равен произведению определителей.

Геометрическое и алгебраическое определение и формула для нахождения

Формула для вычисления определителя четвертого порядка имеет вид:

\(\left| A\right|=a_{11}M_{11}-a_{12}M_{12}+a_{13}M_{13}-a_{14}M_{14}\)

Алгебраический смысл определителя заключается в том, что определитель матрицы А = (n*n) – является алгебраической суммой n слагаемых.

Формула алгебраического определения определителя имеет вид:

\(det A = \sum_{a_{1},a_{2},...a_{n}}^{}{-1^{N (a_{1},a_{2},...a_{n})}}*a_{1a_{1}}a_{2a_{2}}...a_{na_{n}}\)

Каждое слагаемое является произведением n-элементов, которые взяли по одному из каждой строки и каждого столбца, умноженное на (-1) в степени Np, определяемое, как количество инверсий.

Геометрический смысл понятия заключается в том, что определитель представляет собой объем параллелепипеда, получаемый в том случае, если рассмотреть строки, как вектора, образующие ребра геометрической фигуры.

При этом число строк или столбцов соответствует количеству векторов. Таким образом, в случае матрицы А = (2*2), получается двухмерный параллелограмм, а детерминант является площадью рассматриваемой фигуры. Если А = (3*3), то геометрическая фигура будет иметь вид трехмерного параллелепипеда, а определитель – являться его объемом.

Правильная расстановка индексов в матрице

Каждый элемент обладает парой индексов:

• первый – определяет строку;
• второй – указывает столбец.

Так как порядок представляет собой число строк или столбцов в квадратной матрице, то он определяется с помощью m-индекса нижней строки или n-индекса крайнего правого столбца. Данный метод используют при очень больших таблицах, когда считать строки или столбы неудобно.

Матрица представляет собой таблицу, заполненную числами. Одной из ее ключевых характеристик является размерность, то есть число строк и столбцов, из которых она состоит. Как правило, говорят, что какая-то матрица A имеет размер \(\left[ m\times n \right]\), если в ней имеется m строк и n столбцов. Запись имеет следующий вид:

\(A=\left[ m\times n \right]\)

или  \(A=\left( {{a}_{ij}} \right),\quad 1\le i\le m;\quad 1\le j\le n.\)

Существуют и другие обозначения для матрицы. В любом случае, при разных \(\left[ m\times n \right]\) и \({{a}_{ij}}\) возникает вопрос расстановки индексов. В этом случае целесообразно обратиться к обычной системе координат:

Данная система имеет начало координат (точка \( O=\left( 0;0 \right)\)) оси x и y, а каждая точка на плоскости однозначно определяется по координатам:

\(A=\left( 1;2 \right)\)

\(B=\left( 3;1 \right)\) и так далее.

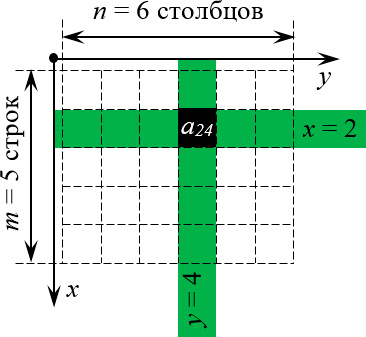
Следует поставить рассматриваемую систему рядом с матрицей, таким образом, чтобы начало координат совпадало с левым верхним углом, что существенно облегчит задачу определения индексов. Оси должны быть направлены так, чтобы охватить всю систему. При этом необходимо повернуть систему координат. Правильный вариант расположения представлен на рисунке:

Получается, что любая клетка матрицы обладает однозначными координатами х и у. К примеру, запись \({{a}_{24}}\) означает, что мы обращаемся к элементу с координатами x=2  и y=4. Размеры матрицы также однозначно заданы двумя числами:

Общая схема вычисления определителей

\(\left| A \right|=\sum{{{M}_{k}}\cdot {{A}_{k}}}\)

При этом подобных слагаемых будет ровно:

\(C_{n}^{k}\)

Следствие из Теоремы Лапласа определяет разложение определителя по строке или столбцу. Пусть в матрице размера \(\left[ n\times n \right]\) выбрана одна строка. Минорами в этой строке будут n отдельных клеток:

\({{M}_{1}}={{a}_{ij}},\quad j=1,...,n\)

Рассчитать дополнительные миноры можно с помощью исключения из начальной матрицы строки и столбца, которые содержат \({{a}_{ij}}\). Следует переименовать данные миноры, как \(M_{ij}^{*}\). Для алгебраического дополнения также требуется число S, однако при миноре первого порядка, оно представляет собой сумму «координат» клетки \({{a}_{ij}}\):

S=i+j

В этом случае начальный определитель допустимо расписать через \({{a}_{ij}} и M_{ij}^{*}\), исходя из теоремы Лапласа:

\(\left| A \right|=\sum\limits_{j=1}^{n}{{{a}_{ij}}\cdot {{\left( -1 \right)}^{i+j}}\cdot {{M}_{ij}}}\)

Таким образом удалось вывести формулу для разложения определителя по строке. Аналогичный метод можно использовать для того, чтобы разложить определитель по столбцам.

Данное следствие позволяет сделать несколько выводов:

• методика подходит для строк и столбцов;
• число слагаемых в разложении в любом случае составляет n;
• вместо одного определителя \(\left[ n\times n \right]\) необходимо вычислить несколько определителей размера на единицу меньше \(\left[ \left( n-1 \right)\times \left( n-1 \right) \right].\)

Практическое применение алгоритма можно продемонстрировать, решая задачу по нахождению определителя матрицы:

\(\left| \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\\end{matrix} \right|\)

В первую очередь необходимо разложить данный определитель по первой строке:

\(\begin{align} \left| A \right|=1\cdot {{\left( -1 \right)}^{1+1}}\cdot \left| \begin{matrix} 5 & 6 \\ 8 & 9 \\\end{matrix} \right|+ & \\ 2\cdot {{\left( -1 \right)}^{1+2}}\cdot \left| \begin{matrix} 4 & 6 \\ 7 & 9 \\\end{matrix} \right|+ & \\ 3\cdot {{\left( -1 \right)}^{1+3}}\cdot \left| \begin{matrix} 4 & 5 \\ 7 & 8 \\\end{matrix} \right|= & \\\end{align}\)

Отсюда следует:

\(\begin{align} &=1\cdot \left( 45-48 \right)-2\cdot \left( 36-42 \right)+3\cdot \left( 32-35 \right)= \\ &=1\cdot \left( -3 \right)-2\cdot \left( -6 \right)+3\cdot \left( -3 \right)=0. \\\end{align}\)

В результате получим ответ: 0.

В другом примере требуется найти определитель:

\(\left| \begin{matrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end{matrix} \right|\)

В данном случае можно рассмотреть вычисление определителя по столбцам. Последний столбец имеет сразу два нуля, что поможет упростить решение задачи. Необходимо разложить определитель по четвертому столбцу:

\(\begin{align} \left| \begin{matrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end{matrix} \right|=0\cdot {{\left( -1 \right)}^{1+4}}\cdot \left| \begin{matrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end{matrix} \right|+ & \\ +1\cdot {{\left( -1 \right)}^{2+4}}\cdot \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end{matrix} \right|+ & \\ +1\cdot {{\left( -1 \right)}^{3+4}}\cdot \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end{matrix} \right|+ & \\ +0\cdot {{\left( -1 \right)}^{4+4}}\cdot \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\\end{matrix} \right| & \\\end{align}\)

От пары слагаемых можно избавиться. В результате останется пара определителей 3х3:

\(\begin{align} & \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 1 & 0 \\ 1 & 1 & 1 \\\end{matrix} \right|=0+0+1-1-1-0=-1; \\ & \left| \begin{matrix} 0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 1 \\\end{matrix} \right|=0+1+1-0-0-1=1. \\\end{align}\)

\(\left| \begin{matrix} 0 & 1 & 1 & 0 \\ 1 & 0 & 1 & 1 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 1 & 0 \\\end{matrix} \right|=1\cdot \left( -1 \right)+\left( -1 \right)\cdot 1=-2\)

В результате вычислений получен ответ: -2

Метод понижения порядка

Упростить расчеты при вычислении определителей можно, используя их свойства. Например, требуется вычислить определитель:

\(\begin{vmatrix}6&3&8&-4\\5&6&4&2\\0&3&4&2\\4&1&-4&6\end{vmatrix}\)

Следует вынести из третьего столбца множитель 4:

\(\begin{vmatrix}6&3&8&-4\\5&6&4&2\\0&3&4&2\\4&1&-4&6\end{vmatrix}=4\cdot\begin{vmatrix}6&3&2&-4\\5&6&1&2\\0&3&1&2\\4&1&-1&6\end{vmatrix}\)

Далее следует вынести из четвертого столбца множитель 2:

\(4\cdot\begin{vmatrix}6&3&2&-4\\5&6&1&2\\0&3&1&2\\4&1&-1&6\end{vmatrix}=4\cdot2\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}\)

Затем можно прибавить к строке №1 строку №2, умноженную на (-2):

\(8\cdot\begin{vmatrix}6&3&2&-2\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}\)

Следующим шагом будет сложение строки №3 и строки №2, умноженной на (-1):

\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\0&3&1&1\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\4&1&-1&3\end{vmatrix}\)

Далее нужно прибавить к четвертой строке вторую, умноженную на 1:

\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\4&1&-1&3\end{vmatrix}=8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\9&7&0&4\end{vmatrix}\)

Можно разложить определитель по третьему столбцу:

\(8\cdot\begin{vmatrix}-4&-9&0&-4\\5&6&1&1\\-5&-3&0&0\\9&7&0&4\end{vmatrix}=8\cdot1\cdot(-1)^{2+3}\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=8\cdot(-1)^{5}\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=-8\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}\)

Если прибавить к первой строке третью, умноженную на 1, получим:

\(-8\begin{vmatrix}-4&-9&-4\\-5&-3&0\\9&7&4\end{vmatrix}=-8\begin{vmatrix}5&-2&0\\-5&-3&0\\9&7&4\end{vmatrix}\)

Затем необходимо разложить определитель по третьему столбцу и вычислить его:

\(-8\begin{vmatrix}5&-2&0\\-5&-3&0\\9&7&4\end{vmatrix}=-8\cdot4\cdot(-1)^{3+3}\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\cdot(-1)^{6}\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}\)

Далее следует прибавить к строке №2 строку №1, умноженную на 1:

\(-32\begin{vmatrix}5&-2\\-5&-3\end{vmatrix}=-32\begin{vmatrix}5&-2\\0&-5\end{vmatrix}\)

При разложении определителя по столбцу №1 и замене определителя 1-го порядка единственным его элементом получим:

\(-32\begin{vmatrix}5&-2\\0&-5\end{vmatrix}=-32\cdot5\cdot(-1)^{1+1}\cdot(-5)=-32\cdot5\cdot1\cdot(-5)=800\)

Приведение к треугольному виду

Методика заключается в приведении определителя к треугольнику. После этого остается вычислить произведение элементов, расположенных на главной диагонали. С помощью данного способа вычислим определитель:

\(\begin{vmatrix}4&-2&0&5\\3&2&-2&1\\-2&1&3&-1\\2&3&-6&-3\end{vmatrix}\)

В первую очередь следует поменять местами первую и третью строки:

\(\begin{vmatrix}4&-2&0&5\\3&2&-2&1\\-2&1&3&-1\\2&3&-6&-3\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\2&3&-6&-3\end{vmatrix}\)

Далее первую строку, умноженную на 1, можно прибавить к четвертой:

\(-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\2&3&-6&-3\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\0&4&-3&-4\end{vmatrix}\)

Затем нужно к строке №3 прибавить строку №1, умноженную на 2:

\(-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\4&-2&0&5\\0&4&-3&-4\end{vmatrix}=-\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)

Следующий шаг – умножение второй строки на 2:

\(\begin{vmatrix}-2&1&3&-1\\3&2&-2&1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\6&4&-4&2\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)

Сложим вторую и первую строку, умноженную на 3:

\(-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\6&4&-4&2\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}\)

После умножения строки №4 на 7 получим:

\(-\frac{1}{2}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&4&-3&-4\end{vmatrix}=-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&28&-21&-28\end{vmatrix}\)

Затем следует прибавить к четвертой строке вторую строку, умноженную на (-4):

\(-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&28&-21&-28\end{vmatrix}=-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&0&-41&-24\end{vmatrix}\)

В результате смены мест столбцов №3 и №4 получим:

\(-\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&3&-1\\0&7&5&-1\\0&0&6&3\\0&0&-41&-24\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&-24&-41\end{vmatrix}\)

После того, как третья строка, умноженная на 8, будет прибавлена к четвертой строке, получится вычислить определитель:

\(\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&-24&-41\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\begin{vmatrix}-2&1&-1&3\\0&7&-1&5\\0&0&3&6\\0&0&0&7\end{vmatrix}=\frac{1}{2}\cdot\frac{1}{7}\cdot(-2)\cdot7\cdot3\cdot7=-21\)