Сечение цилиндра: определение, виды, его образующая
Кратко о цилиндре
Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.
Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.
Осевое сечение
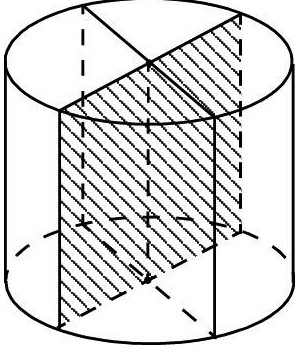
Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти площадь сечения
Формула 1
\(S = d*h,\)
где \(d\) — диаметр, а \(h\) — высота всей фигуры.
Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).
Формула 2
\(S = a*h, \)
где \(a\) — хорда.
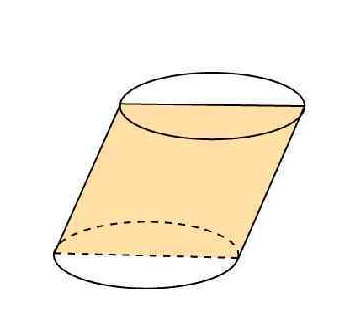
Осевое сечение наклонного цилиндра
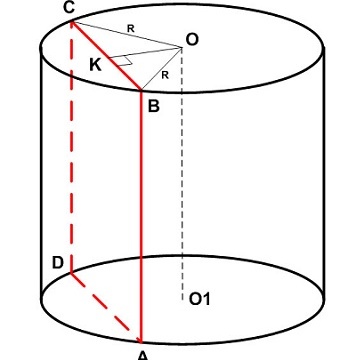
Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.
Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:
\(S = d * b * sin(α)\)
Примеры задач
Рассмотрим пару задач на осевое сечение с решениями.
Задача 1
Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?
Решение
Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:
\(Sц = 2pi * r * (r + h)\)
Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:
\(Sц = 2pi * r * (r + 2r) = 6 * pi * r²\)
Исходя из этого, будем выражать радиус:
\(r = √(Sц / (6*pi))\)
Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:
\(S = (2*r)2 = 4*r2 = 2*Sц/ (3*pi)\)
Подставим известные данные (\(Sц = 100см^2\)) и получим площадь сечения \(S = 21,23 см²\).
Ответ: \(S = 21,23 см²\).
Задача 2
Дано: ABCD — осевое сечение цилиндра. Площадь сечения \(Sc\) равна \(10 м²\), а площадь основания \(Sо— 5 м²\). Найти высоту цилиндра.
Решение
Так как площадь основания — круг, то \(Sо = pi * r²\). Тогда \(r = √(Sо/pi) = √(5/pi).\)
Так как площадь сечения — прямоугольник, то \(Sc = AB * BC = h * 2r.\) Тогда \(h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).\)
Ответ: \(h = √(5pi).\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так