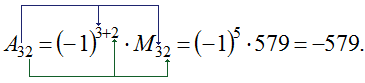Минор и алгебраическое дополнение матрицы
Что такое минор и алгебраическое дополнение матрицы
Минор Mij к элементу aij определителя n-го порядка является определителем (n−1)-го порядка, получающимся из начального определителя после исключения i-той строки и j-того столбца.
Исходя из определения, минор представляет собой определитель, который остается после того, как вычеркнуть конкретную строку и конкретный столбец. К примеру, M12 будет получен в результате устранения первой строки и второго столбца. Для того чтобы получить M34 следует вычеркнуть третью строку и четвертый столбец.
Найти миноры с помощью вычерков можно, следуя алгоритму:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- устранение i-ой строки;
- вычерк j-ого столбца;
- запись определителя, который получился по итогам проделанных манипуляций.
Алгебраическое дополнение Aij к элементу aij определителя n-го порядка представляет собой число \(A_{ij}=(-1)^{i+j}Mij\), в котором i, j являются соответствующими строкой и столбцом, а Mij — минором к рассматриваемому элементу.
Порядок действия при определении алгебраического дополнения следующий:
- определение суммы номеров строки ( i ) и столбца ( j );
- поиск минора Mij, с помощью применения алгоритма вычисления миноров, который был рассмотрен выше;
- подстановка значений, которые были получены на первом и втором этапах расчета, в формулу \(A_{ij}=(-1)^{i+j}Mij.\)
Общие понятия, основные формулы
Предположим, что существует какая-то квадратная матрица или квадратная матрица n-го порядка:
\(A_{n\times n}\)
\(Минор \ M_{ij} \ элемента \ a_{ij} \ матрицы \ A_{n\times n}\) будет являться определитель матрицы, которая получается из матрицы A в результате устранения i-й строки и j-го столбца, которые расположены таким образом, что их пересечение совпадает с элементом \(a_{ij}.\)
В качестве доказательства можно рассмотреть такую квадратную матрицу четвертого порядка:
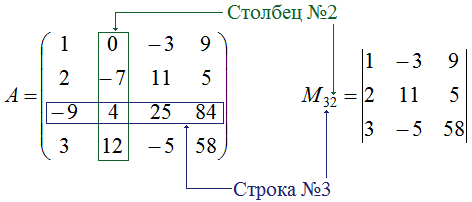
\(A=\left( \begin{array} {cccc} 1 & 0 & -3 & 9\\ 2 & -7 & 11 & 5 \\ -9 & 4 & 25 & 84\\ 3 & 12 & -5 & 58 \end{array} \right)\)
Необходимо определить минор для элемента \(a_{32}\), то есть \(M_{32}\). В первую очередь следует записать минор \(M_{32}\), а затем рассчитать его. Порядок действий для составления \(M_{32}\) включает вычерк из матрицы A третьей строки и второго столбца. Данное действие обусловлено тем, что элемент \(a_{32}\) расположен там, где третья строка и второй столбец пересекаются. Таким образом, была получена новая матрица с определителем в виде искомого минора \(M_{32}\).
Данный минор достаточно просто рассчитать с помощью теоремы для вычисления определителей второго и третьего порядков. Расчет будет следующий:
\(M_{32}=\left| \begin{array} {ccc} 1 & -3 & 9\\ 2 & 11 & 5 \\ 3 & -5 & 58 \end{array} \right|= 1\cdot 11\cdot 58+(-3)\cdot 5\cdot 3+2\cdot (-5)\cdot 9-9\cdot 11\cdot 3-(-3)\cdot 2\cdot 58-5\cdot (-5)\cdot 1=579\)
Таким образом, минор элемента \(a_{32}\) равен 579, то есть \(M_{32}=579\)
Нередко в тематической литературе вместо «минор элемента матрицы» употребляют понятие «минор элемента определителя». Смысл выражения сохраняется. Таким образом, для вычисления минора элемента \(a_{ij}\) требуется исключить из начального определителя i-ю строку и j-й столбец. Элементы, которые остались, следует записать в новый определитель, который представляет собой минор элемента \(a_{ij}.\)
В качестве примера можно рассчитать минор элемента \(a_{12}\) определителя:
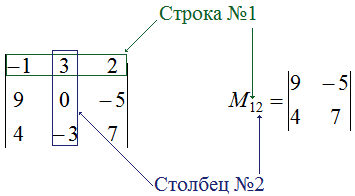
\(\left| \begin{array} {ccc} -1 & 3 & 2\\ 9 & 0 & -5 \\ 4 & -3 & 7 \end{array} \right|\)
В первую очередь нужно записать искомый минор \(M_{12}\). Для этого можно исключить из заданного определителя первую строку и второй столбец:
Вычислить минор целесообразно с помощью формулы для расчета определителей второго и третьего порядков:
\(M_{12}=\left| \begin{array} {cc} 9 & -5\\ 4 & 7 \end{array} \right|=9\cdot 7-(-5)\cdot 4=83\)
В результате минор элемента \(a_{12}\) составит 83, то есть \(M_{12}=83\)
Предположим, что существует какая-то квадратная матрица \(A_{n\times n}\), то есть квадратная матрица n-го порядка. Алгебраическое дополнение \(A_{ij}\) элемента \(a_{ij}\) матрицы \(A_{n\times n}\) можно определить, используя формулу:
\(A_{ij}=(-1)^{i+j}\cdot M_{ij},\)
где \(M_{ij}\) является минором элемента \(a_{ij}.\)
В качестве примера можно рассчитать алгебраическое дополнение элемента \(a_{32}\) матрицы:
\(A=\left( \begin{array} {cccc} 1 & 0 & -3 & 9\\ 2 & -7 & 11 & 5 \\ -9 & 4 & 25 & 84\\ 3 & 12 & -5 & 58 \end{array} \right)\)
В результате необходимо получить значение для \(A_{32}\). В предыдущем примере уже был расчет для минора \(M_{32}=579\), поэтому целесообразно в данной задаче использовать имеющиеся данные:
Как правило, при определении алгебраических дополнений не требуется выполнять отдельный расчет минора перед вычислением непосредственно дополнения. К примеру, если требуется определить \(A_{12}\) при условии, что:
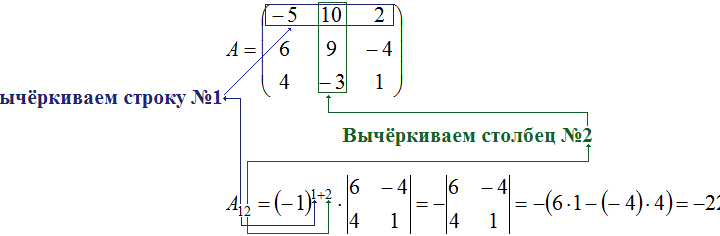
\(A=\left( \begin{array} {ccc} -5 & 10 & 2\\ 6 & 9 & -4 \\ 4 & -3 & 1 \end{array} \right)\)
Необходимо записать справедливое равенство:
\(A_{12}=(-1)^{1+2}\cdot M_{12}=-M_{12}\)
Рассчитать \(M_{12}\) легко с помощью вычерка первой строки и второго столбца матрицы А. Поэтому нет необходимости вводить лишнее обозначение для минора. Достаточно сразу записать уравнение для алгебраического дополнения \(A_{12}\):
Решение миноров и алгебраических дополнений
Миноры и алгебраические дополнения встречаются в задачах не только с квадратными матрицами, но и прямоугольными. Во втором случае матрицы отличаются тем, что количество строк не обязательно совпадает с количеством столбцов. К примеру, записана матрица:
\(A_{m\times n}\)
В рассматриваемой матрице m строк и n столбцов. Минор k-го порядка матрицы \(A_{m\times n}\) представляет собой определитель с элементами, расположенными на пересечении k строк и k столбцов матрицы A. Следует учитывать, что при этом k≤ m и k≤ n.
В качестве примера можно рассмотреть матрицу:
\(A=\left( \begin{array} {cccc} -1 & 0 & -3 & 9\\ 2 & 7 & 14 & 6 \\ 15 & -27 & 18 & 31\\ 0 & 1 & 19 & 8\\ 0 & -12 & 20 & 14\\ 5 & 3 & -21 & 9\\ 23 & -10 & -5 & 58 \end{array} \right)\)
Можно записать для нее какой-то минор третьего порядка. Для этого следует отобрать какие-то три строки и три столбца рассматриваемой матрицы. Выберем для расчета строки №2, №4, №6 и столбцы №1, №2, №4. Данные строки и столбцы будут пересекаться в том месте, где расположены элементы искомого минора.
\(M=\left|\begin{array} {ccc} 2 & 7 & 6 \\ 0 & 1 & 8 \\ 5 & 3 & 9 \end{array} \right|.\)
Расположение миноров первого порядка будет совпадать с пересечением одной строки и одного столбца. Таким образом, выводим равенство миноров первого порядка элементам рассматриваемой матрицы.
Минор k-го порядка матрицы \(A_{m\times n}=(a_{ij})\) является ключевым в том случае, когда главная диагональ рассматриваемого минора включает исключительно ключевые диагональные элементы матрицы A.
Главные диагональные элементы представляют собой такие элементы матрицы, которые содержат индексы, равные\( a_{11}, a_{22}, a_{33}\) и так далее. К примеру, матрица А, которая рассматривается в примере, содержит элементы \(a_{11}=-1, a_{22}=7, a_{33}=18, a_{44}=8.\)
\(\left( \begin{array} {cccc} {-1} & 0 & -3 & 9\\ 2 &{7} & 14 & 6 \\ 15 & -27 & {18} & 31\\ 0 & 1 & 19 & {8}\\ 0 & -12 & 20 & 14\\ 5 & 3 & -21 & 9\\ 23 & -10 & -5 & 58 \end{array} \right)\)
В том случае, когда в матрице А исключены строки и столбцы, которые соответствуют номерам 1 и 3, их пересечение будет совпадать с элементами минора второго порядка. Главная диагональ этого минора будет содержать лишь диагональные элементы матрицы А. К примеру, такими элементами являются элементы \( a_{11}=-1\) и \(a_{33}=18\) матрицы A. Таким образом, главный минор второго порядка будет равен:
\(M=\left|\begin{array} {cc} {-1} & -3 \\ 15 & {18} \end{array} \right|\)
В том случае, если выбрать строки и столбцы с другими номерами, получится другой главный минор второго порядка.
Можно предположить, что какой-то минор M k-го порядка матрицы A_{m\times n} обладает ненулевым значением, то есть M\neq 0. В данном случае, для всех миноров с порядками выше, чем k, справедливо равенство нулю. Тогда минор M является базисным, а строки и столбцы, содержащие элементы базисного минора, носят названием базисных строк и базисных столбцов.
В качестве примера можно рассмотреть следующую матрицу:
\(A=\left( \begin{array} {ccc} -1 & 0 & 3 & 0 & 0 \\ 2 & 0 & 4 & 1 & 0\\ 1 & 0 & -2 & -1 & 0\\ 0 & 0 & 0 & 0 & 0 \end{array} \right)\)
Запись минора рассматриваемой матрицы с элементами, распложенными на месте, где пересекаются строки №1, №2, №3 и столбцы №1, №3, №4, представляет собой минор третьего порядка и имеет следующий вид:
\(\; M=\left|\begin{array} {ccc} -1 & 3 & 0 \\ 2 & 4 & 1 \\ 1 & -2 & -1 \end{array} \right|\)
Рассчитать значение искомого минора можно, используя правило для расчета определителей второго и третьего порядков:
\(M=\left| \begin{array} {ccc} -1 & 3 & 0\\ 2 & 4 & 1 \\ 1 & -2 & -1 \end{array} \right|=4+3+6-2=11\)
В результате:
\(M=11\neq 0\)
Далее можно попытаться записать какой-либо минор с порядком выше, чем 3. Для составления минора четвертого порядка необходимо воспользоваться четвертой строкой, элементы которой имеют нулевые значения. Исходя из этого, можно заключить, что любой минор четвертого порядка обладает нулевой строкой. Таким образом, значение каждого из миноров четвертого порядка равно нулю. Записать миноры пятого порядка и выше не представляется возможным по причине наличия в матрице А всего четырех строк.
По результатам вычислений удалось определить минор третьего порядка с ненулевым значением. Одновременно с этим, миноры более высоких порядков равны нулю, из чего можно сделать вывод: рассматриваемый минор является базисным. Строки №1, №2, №3 матрицы А, которые содержат элементы данного минора, являются базисными строками, а столбцы №1, №3, №4 матрицы А — базисными столбцами.
Пример, который был рассмотрен, является тривиальным. Однако с его помощью удобно продемонстрировать смысл базисного минора. В реальных условиях базисных миноров может быть более одного, а решение подобных задач на нахождение подобного минора существенно сложнее и объемнее.
Еще одним важным термином является окаймляющий минор. Для раскрытия понятия можно предположить, что какой-то минор k-го порядка M матрицы \(A_{m\times n}\) находится в месте, где пересекаются k строки и k столбцы. Если прибавить к совокупности данных строк и столбцов дополнительные строку и столбец, то минор (k+1)-го порядка, который получился в результате, представляет собой окаймляющий минор для минора M.
В качестве примера можно рассмотреть матрицу:
\(A=\left( \begin{array} {ccccc} -1 & 2 & 0 & -2 & -14\\ 3 & -17 & -3 & 19 & 29\\ 5 & -6 & 8 & -9 & 41\\ -5 & 11 & 19 & -20 & -98\\ 6 & 12 & 20 & 21 & 54\\ -7 & 10 & 14 & -36 & 79 \end{array} \right)\)
В первую очередь нужно записать минор второго порядка с элементами, расположенными в месте, где пересекаются строки №2 и №5, а также столбцы №2 и №4.
\(M=\left|\begin{array} {ccc} -17 & 19 \\ 12 & 21 \end{array} \right|\)
К комплекту строк с элементами минора М требуется прибавить одну строку №1, а к столбцам — столбец №5. В результате манипуляций получится новый минор M' третьего порядка с элементами, расположенными там, где пересекаются строки №1, №2, №5 и столбцы №2, №4, №5.
\(M'=\left|\begin{array} {ccc} 2 & -2 & -14 \\ -17 & 19 & 29 \\ 12 & 21 & 54 \end{array} \right|\)
Минор M' представляет собой окаймляющий минор для минора M. Таким же образом, путем добавления к комплекту строк с элементами минора М строки №4, а к совокупности столбцов — столбца №3, можно записать минор M'', то есть минор третьего порядка.
\( M''=\left|\begin{array} {ccc} -17 & -3 & 19 \\ 11 & 19 & -20 \\ 12 & 20 & 21 \end{array} \right|.\)
Минор M'', аналогично предыдущему, представляет собой окаймляющий минор для минора M.
Предположим, что существует какой-то минор M k-го порядка матрицы \(A_{n\times n}.\)
Определитель (n-k)-го порядка с элементами, полученными из матрицы A путем исключения строк и столбцов, которые содержали минор M, называется минором, дополнительным к минору M.
В качестве примера можно рассмотреть квадратную матрицу пятого порядка:
\(A=\left( \begin{array}{ccccc} -1 & 2 & 0 & -2 & -14\\ 3 & -17 & -3 & 19 & 29\\ 5 & -6 & 8 & -9 & 41\\ -5 & 11 & 16 & -20 & -98\\ -7 & 10 & 14 & -36 & 79 \end{array} \right)\)
В рассматриваемой матрице можно выбрать строки №1 и №3, столбцы №2 и №5. Пересечение данных строк и столбцов будет совпадать с элементами минора М второго порядка.
\( M=\left|\begin{array}{cc} 2 & -14 \\ -6 & 41 \end{array} \right|\)
Далее следует исключить из матрицы А строки №1 и №3, а также столбцы №2 и №5. На пересечении данных компонентов расположены элементы минора М. Элементы, которые остались нетронутыми, сформируют минор M'.
\(M'=\left|\begin{array} {ccc} 3 & -3 & 19 \\ -5 & 16 & -20 \\ -7 & 14 & -36 \end{array}\right|\)
Минор M' с порядком, соответствующим 5-2=3, представляет собой минор, являющийся дополнительным к минору M.
Запись алгебраического дополнения к минору M квадратной матрицы \(A_{n\times n}\) имеет следующий вид:
\((-1)^{\alpha}\cdot M'\)
В данном случае \alpha является суммой номеров строк и столбцов матрицы A, содержащих элементы минора M, а M' является дополнительным к минору M. Термин «алгебраическое дополнение к минору M», как правило, формулируют таким образом: «алгебраическое дополнение минора M».
В качестве примера можно рассмотреть матрицу А. Ранее для рассматриваемой матрицы был определен в ходе расчетов минор второго порядка:
\(M=\left| \begin{array} {ccc} 2 & -14 \\ -6 & 41 \end{array} \right|\)
Дополнительным к данному минору является такой минор третьего порядка:
\(M'=\left| \begin{array} {ccc} 3 & -3 & 19\\ -5 & 16 & -20 \\ -7 & 14 & -36 \end{array} \right|\)
В качестве обозначения алгебраического дополнения минора M целесообразно использовать: M^*
Исходя из определения, получим:
\(M^*=(-1)^\alpha\cdot M'\)
Параметр \alpha представляет собой сумму номеров строк и столбцов, которым соответствует минор М. Расположение данного минора соответствует пересечению строк №1, №3 и столбцов №2, №5. Таким образом:
\(\alpha=1+3+2+5=11\)
В результате можно записать:
\(M^*=(-1)^{11}\cdot M'=-\left| \begin{array} {ccc} 3 & -3 & 19\\ -5 & 16 & -20 \\ -7 & 14 & -36 \end{array} \right|\)
Благодаря формуле для расчета определителей второго и третьего порядков, представляется возможным вычислить алгебраическое дополнение:
\(M^*=-\left| \begin{array} {ccc} 3 & -3 & 19\\ -5 & 16 & -20 \\ -7 & 14 & -36 \end{array} \right|=-30\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так