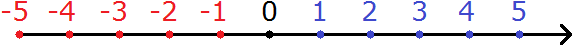Положительные и отрицательные числа

Какие числа называются положительными и отрицательными

Отрицательными числами в алгебре являются числа со знаком минус (-). Например, к таким числам относят -1, -2, -3. Прочитать запись можно, как минус один, минус два, минус три.

В системе отрицательных чисел так же, как и среди положительных есть дроби: обыкновенные и десятичные, целые числа, корни и так далее. Почти все подвиды чисел, которые встречаются среди положительных чисел, есть и среди отрицательных. Стоит отметить, что, согласно понятию, число 0 не является ни положительным, ни отрицательным числом.

Наглядным примером использования отрицательных чисел является термометр. Прибор демонстрирует температуру тела, воздуха, почвы, воды. Зимой при холодной погоде температура воздуха снижается до отрицательных значений. К примеру, -10 градусов мороза:

Обычные числа, в том числе, 1, 2, 3 называют положительными. Данные числа имеют знак (+). Обычно, его не записывают.

Координатная прямая имеет следующий вид:

В данном случае отмечены только числа от −5 до 5. В действительности координатная прямая бесконечна. На изображении можно увидеть только фрагмент этой прямой. Для того чтобы отметить на координатной прямой числа, использую точки. Началом отсчета является нуль. С левой стороны от нуля отмечают отрицательные числа, а с правой — положительные.

Координатная прямая продолжается бесконечно по обе стороны. Бесконечность в математике обозначается символом   \(\infty\). Отрицательное направление будет обозначаться символом −\(\infty\), а положительное — символом +\(\infty\). Таким образом, координатная прямая содержит все числа от минус бесконечности до плюс бесконечности:

\((−\infty; +\infty)\)

Каждая точка на координатной прямой обладает определенным именем и координатой. Именем является какая-либо латинская буква. Координата представляет собой число, указывающее на положение точки на прямой. Таким образом, координатой является то число, которое требуется отметить на координатной прямой. К примеру, точка А(2) читается, как «точка А с координатой 2» и обозначается на координатной прямой таким образом:

При рассмотрении изображения координатной прямой можно заметить, что отрицательные числа лежат левее относительно начала отсчета, а положительные числа — правее. С каждым шагом в левую сторону число будет уменьшаться в меньшую сторону. При каждом шаге в правом направлении число будет увеличиваться.

Сравнение положительных и отрицательных чисел

Положительные числа, то есть те, которые больше 0, можно рассматривать в качестве прибыли, прибавки, увеличения количества чего-либо. Отрицательные числа можно представить, как недостаток, убыток, расход, долг. Предположим, что имеется 55 неких предметов, например, яблок. Цифра 55 является положительной. В том случае, когда требуется отдать кому-то 5 яблок, данной действие можно обозначить, как -5. На градуснике рост температуры на 4,5 значений можно описать как +4,5, а снижение, в свою очередь, как −4,5. В приборах, которые используют для измерений, часто применяют положительные и отрицательные числа. Это объясняется удобством отображения изменения величин.

Любое отрицательное число меньше, чем любое положительное число. К примеру, если сравнить -5 и 3, то минус пять меньше трех. Это объясняется тем, что -5 представляет собой отрицательное число, а 3 является положительным числом. С помощью координатной прямой достаточно просто определить положение данных чисел.

На прямой -5 расположено левее относительно числа 3. Согласно правилу, любое отрицательное число меньше любого положительного числа. Отсюда следует, что:

−5 < 3

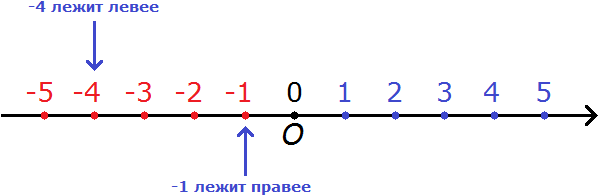
Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. К примеру, при сравнении чисел -4 и -1 можно сделать вывод, что минус четыре меньше, чем минус единица. Причина заключается в том, что на координатной прямой -4 располагается левее, чем -1.

Видно, что -4 лежит левее, а -1 правее. Из двух отрицательных чисел меньше то, которое располагается левее на координатной прямой. Таким образом:

-4 < -1

Ноль больше, чем любое отрицательное число. К примеру, при сравнении 0 и -3 можно сделать вывод, что ноль больше, чем минус три. Это объясняется тем, что на координатной прямой 0 располагается правее, чем -3.

При рассмотрении координатной прямой можно заметить, что 0 лежит правее, а -3 левее. Согласно правилу, нуль больше любого отрицательного числа. Таким образом:

0 > -3

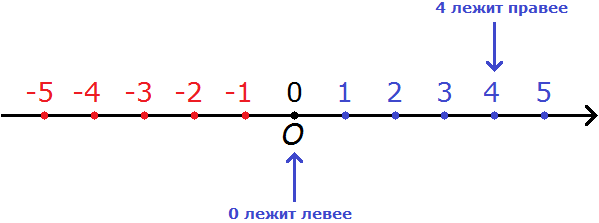
Нуль меньше любого положительного числа. К примеру, можно сравнить 0 и 4. Ноль меньше, чем 4.

На координатной прямой 0 располагается левее, а 4 правее. Исходя из правила, ноль меньше, чем какое-либо положительное число. Таким образом:

0 < 4

Правила действий с отрицательными и положительными числами

Существуют следующие правила знаков при умножении и делении отрицательных чисел:

1. Умножение или деление отрицательного числа на отрицательное приводит в результате к получению положительного числа.
2. При умножении или делении положительного числа на отрицательное число результатом является отрицательное число.
3. Если требуется умножить или разделить отрицательное число на положительное, то получится отрицательное число.

В процессе сложения отрицательных чисел следует руководствоваться аналогичными правилами знаков в несколько ином виде. По общей формулировке правило знаков звучит так: «Плюс на минус дает минус, минус на минус дает плюс и плюс на плюс дает плюс». В таком случае, при сложении отрицательного числа с другим, получится:

-а+(-в)=-а-в — то есть из отрицательного числа вычитается положительное.

Аналогичное правило применимо для примеров с вычитанием отрицательных чисел:

-а-(-в)=-а+в — к отрицательному числу в итоге прибавляется положительное.

В том случае, когда требуется сложить два отрицательных числа, следует сложить два числа и поставить знак минус. К примеру:

(−2)+(−3)=−5(−2)+(−3)=−5

Если первое число положительное, а второе отрицательное, требуется определить, какое число по модулю больше. Далее нужно отнять от большего меньшее число и поставим знак большего числа. Например:

(−8)+4=4−8=−4

9+(−4)=9−4=5

Каждое число, за исключением 0, соответствует противоположному элементу. В сумме с ним число дает 0. Например:

−9+9=0

7,1+(−7,1)=0

При вычитании двух отрицательных чисел следует руководствоваться правилом: минус на минус дает плюс. Таким образом, когда стоят рядом два минуса, в сумме получается плюс. К примеру:

(−7)−(−6)=(−7)+6=(−1)

В том случае, когда первое число положительное, а второе число является отрицательным, вычитание выполняют по тому же принципу, что и сложение. Нужно определить, какое число по модулю больше. Далее следует отнять от большего меньшее число и поставить знак большего числа.

7−9=−2

так как 9>7

Одним из ключевых свойств является то, что минус на минус дает плюс:

7−(−9)=7+9=16

Примеры задач с решением

Задача 1

Задача 2

Задача 3

Задача 4

Задача 5

Задача 6

Задача 7

Задача 8

Задача 9

Задача 10

Задача 11

Задача 12

Задача 13

Задача 14

Задача 15

Задача 16