Парабола в математике: уравнение, построение, виды
Что такое парабола в математике
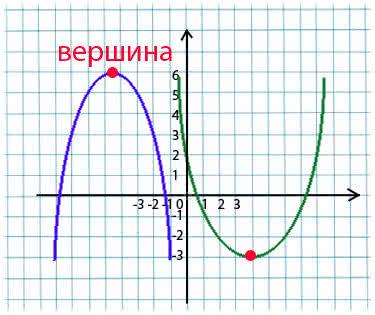
Парабола - график квадратичной функции вида \(f(x)=ax^2+bx+c\). Состоит данный график из вершины и ветвей.
При этом \(a\neq0\), иначе функция уже будет не квадратичной, а линейной.
Формула параболы может рассказать нам о многом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Коэффициент \(a\) говорит о направлении ветвей параболы. Если \(а>0\), то ветви смотрят вверх, если \(а<0\), вниз.
- От параметра \(b\) зависит вершина параболы. Она рассчитывается по формуле: \(x_в=\frac{-b}{2a}\)
- Свободный член \(с\) отвечает за пересечение параболы с осью \(y\).
Алгоритм построения параболы
Построим график функции \(f(x)=ax^2+bx+c.\)
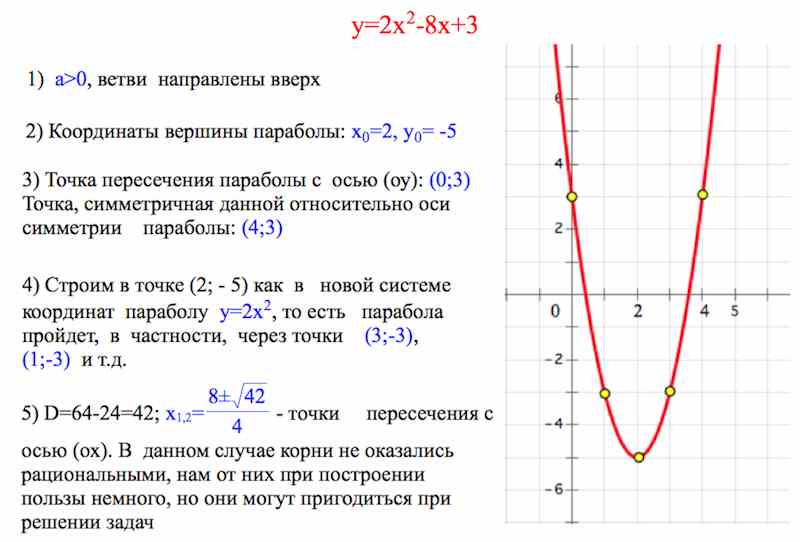
- Определим куда смотрят ветви параболы.
- Найдем вершину по формуле \(x_в=\frac{-b}{2a}\). Подставим \(x_в\) в формулу функции и получим значение \(y_в\). Таким образом мы имеем обе координаты вершины. Нанесем их на систему координат.
- Найдем точку пересечения с осью y по параметру с и нанесем на чертеж точку, симметричную ей, относительно оси симметрии параболы, т.е. прямой \(y=\frac{-b}{2a}.\)
- Далее решаем уравнение \(ax^2+bx+c=0\). Получаем корни - они являются точками пересечения параболы с осью \(x\). Если они рациональны, наносим их на чертеж, в обратном случае, они не пригодятся.
- Затем считаем значения функции в дополнительных симметричных точках и соединяем все найденные точки.
Примеры решения задач на построение параболы
Смещение параболы
Свободный член с смещает параболу по оси y. Например, если c=2, то парабола f(x)=ax^2+bx сместится вверх на 2 единичных отрезка, а если с=-2, то график сместится вниз так же на 2 единичных отрезка.
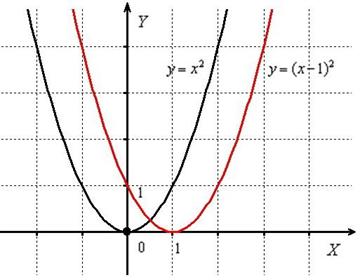
В случае, когда к аргументу x прибавляется или вычитается какое-либо число, график смещается по оси x. Например, для построения графика функции \(y={(x+4)}^2\) достаточно сместить график \(y=x^2 \)на 4 единичных отрезка влево, а для построения графика \(y={(x-3)}^2\) нужно сместить график \(y=x^2\) на 3 единичных отрезка вправо.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так