Измерения прямоугольного параллелепипеда и его свойства
Что такое прямоугольный параллелепипед — определение
Параллелепипед — это призма с шестью гранями, в основании которой лежит параллелограмм.
Согласно другому определению, это многогранник, состоящий из шести сторон-параллелограммов.
В математике в целом, и в геометрии в частности, выделяют несколько основных видов параллелепипеда:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- прямоугольный;
- прямой — параллелепипед, у которого 4 боковые грани являются прямоугольниками;
- наклонный — боковые грани объемной фигуры не перпендикулярны основаниям;
- ромбоэдр — шестигранная призма, грани которой — это ромбы;
- куб — состоит из квадратных граней.
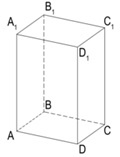
Прямоугольный параллелепипед — это шестигранная призма, каждая из сторон которой в общем случае является прямоугольником. Также это — многогранник, в основании которого лежит прямоугольник, а боковые грани перпендикулярны основанию.
Прямоугольных параллелепипедов в окружающем человека мире множество: комната, закрытая книга, системный блок компьютера, закрытая коробка для подарка, спичечный коробок и т. д.
Прямоугольный параллелепипед, как и любой другой, состоит из:
- основания;
- граней — противоположных, т. е. не имеющих общего ребра, и смежных — тех, которые имеют общее ребро;
- ребер — отрезков, соединяющих соседние вершины объемной шестигранной фигуры;
- диагоналей — отрезков, соединяющих противоположные вершины;
- диагоналей граней;
- высоты — отрезка, соединяющего верхнее и нижнее основания шестигранной призмы.
В некоторых базовых задачах просят найти количество составляющих элементов шестигранной призмы. Эти числа можно запомнить: объемная фигура состоит из 8 вершин, 12 ребер и 6 граней.
Измерениями прямоугольного параллелепипеда называют его длину, ширину и высоту.
Свойства параллелепипеда, какими обладают противолежащие грани
Вне зависимости от вида параллелепипеда, все они обладают 4 свойствами:
- Противолежащие грани равны друг другу и попарно параллельны.
- Все 4 диагонали шестигранника пересекаются в одной точке, которой делятся пополам. Любой отрезок, проходящий через середину диагонали, и концы которого принадлежат поверхности, также делится пополам.
- Фигура симметрична относительно середины диагонали.
- Квадрат длины диагонали равен сумме квадратов трех измерений.
Прямоугольный параллелепипед обладает всеми этими свойствами и несколькими специфичными, свойственными только ему.
- Все стороны — прямоугольники.
- Все углы, состоящие из двух граней, равны 90°.
- Любую сторону можно принять за основание.
- Если все ребра равны и перпендикулярны, то такой шестигранник считается кубом.
Формулы вычисления объема и площади поверхности прямоугольного параллелепипеда
Объем прямоугольного параллелепипеда равен длине, умноженной на ширину и высоту.
\(V=a\cdot b\cdot h,\)
где V — объем, a — длина, b — ширина, h — высота.
Площадь боковой поверхности равна сумме площадей боковых граней.
\(S_{бп}=2(ab+ac)\)
Площадь полной поверхности равна сумме площадей боковых граней и оснований.
\(S_{пп}=2(ab+bc+ac)\)
Как найти диагональ и ширину прямоугольного параллелепипеда
В соответствии с одним из основных свойств параллелепипеда, квадрат длины диагонали равен сумме квадратов трех измерений. Запишем в виде формулы:
\(d^2=a^2+b^2+c^2\)
Следовательно, длина диагонали равна квадратному корню из суммы трех измерений фигуры:
\(sqrt{a^2+b^2+c^2}\)
Длина, ширина и высота, как правило, вычисляются через формулу объема:
\(a=\frac V{bh},\;b=\frac V{ah},\;h=\frac V{ab}\)
Существует и второй вариант, как возможно найти одно из измерений. Если известно смежное ему измерение и диагональ общей стороны шестигранника, то можно вычислить вторую сторону через теорему Пифагора или по свойствам диагонали.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так