Определение параллельных прямых в пространстве

Что такое параллельные прямые в пространстве

Прямые в пространстве могут быть параллельны, пересекаться или скрещиваться. Мы рассмотрим первое свойство.

Впервые теорию о параллельности научно обосновал греческий ученый Евклид в своей работе под названием  «Начала».

Обозначение параллельных прямых

Сами прямые обозначаются латинскими буквами. Например, l и k. Параллельность обозначается символом: ||

Теорема о параллельных прямых, формулировка

Доказательства закона представим в заключительном разделе статьи.

Типы углов при параллельных прямых

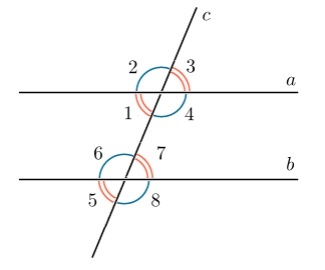
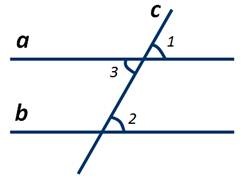
Когда прямая пересекает две другие параллельные друг другу прямые, образуется восемь углов. В геометрии они имеют свои названия и свойства. Для дальнейшего разбора темы этой статьи достаточно разобраться в трех видах. Далее при рассмотрении каждого вида в отдельности ориентируйтесь на рисунок ниже:

Односторонние

 На рисунке выше это ∠1 и ∠6, а также ∠4 и ∠7. Они расположены с одной стороны относительно прямых.

Соответственные

Углы 2 и 6, 3 и 7, 1 и 5, 4 и 8. Их расположения отличается тем, что они как бы разделены между собой одной из прямых.

Накрест лежащие

На данном рисунке это ∠3 и ∠5, ∠2 и ∠8, ∠1 и ∠7, ∠4 и ∠6. Их расположение легко запомнить, так как они размещаются по принципу «крест-накрест».

Условия параллельности

Чтобы доказать параллельность прямых, нужно знать признаки, по которым она определяется. Достаточно соблюдения хотя бы одного из нижеследующих условий.

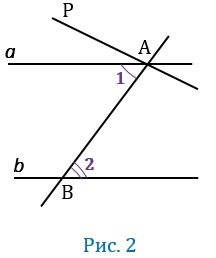
Накрест лежащие углы равны

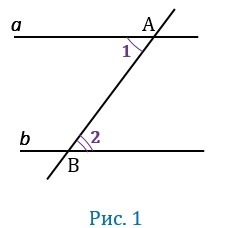
Дано:  \(a\;\vert\vert b\), AB является секущей, углы 1 и 2 — накрест лежащими.

Доказать: равенство ∠1 и ∠2.

Доказательство: допустим, что ∠1 и ∠2 не равные. Тогда проведем угол PAB, причем он будет накрестлежащим с ∠2.

Накрест лежащие углы равны. Из этого следует, что AP \(\vert\vert\) b. Но это невозможно, потому что через точку a может проходить только одна прямая, согласно аксиоме, а у нас получилось две — b и A. Поэтому наше предположение неправильное и ∠1=∠2. Ч.т.д.

Соответственные углы равны

∠1 и ∠2 являются соответственными.

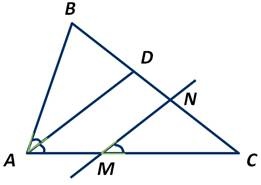
Задача

MN \(\vert\vert\) AD. Доказать, что\( \angle NMC=\angle BAD\).

Решение: \(\angle NMC=\angle DAC\) (как соотв.), а \(\angle DAC=\angle BAD\) (AD — биссектриса). Следовательно, \(\angle NMC=\angle BAD\).

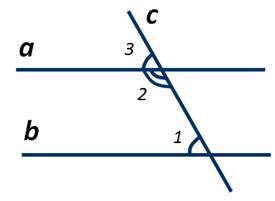
Сумма односторонних углов равна 180 градусов

Сумма ∠1 и ∠2 равна 180º

Доказательство:

a \(\vert\vert\) b, поэтому ∠1=∠3 (соотв.). ∠2+∠3=180º (смеж.). Поэтому при сложении получаем 180º.

Если обе прямые параллельны третьей

Этот признак называют также теоремой о трех параллельных прямых на плоскости. Если a \(\vert\vert\) b и c \(\vert\vert\) b, то a \(\vert\vert\) c.

Доказательство

Есть a \(\vert\vert\) b. Допустим, что существует еще c \(\vert\vert\) a. Согласно условию, a не пересекает b и наоборот.

В трехмерном пространстве прямые, параллельные третьей, параллельны друг с другом

Здесь то же самое, что в предыдущем пункте: в случае, когда a и c ||, а b и c также ||, то a и b тоже ||.

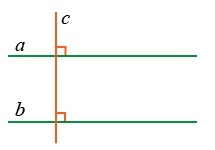
Две прямые, перпендикулярные третьей, параллельны

Обозначение перпендикулярных прямых: ⊥

На картинке видно, что a \(\perp\) c и b \(\perp\) c. Отсюда, согласно этому признаку-теореме, следует, что a \(\vert\vert\) b.

Доказательство

Допустим, что a \(\perp\) c и b \(\perp\) c, но a не \(\vert\vert\;\)b. Тогда a и b пересекаются в какой-то точке. Рассмотрим треугольник ABC. Сумма его углов будет равна 180º+∠C. Но так быть не может. Значит, наше предположение неверно, и a \(\vert\vert\) b.

Доказательство параллельности прямых

Ниже представлено доказательство теоремы из первого раздела статьи.

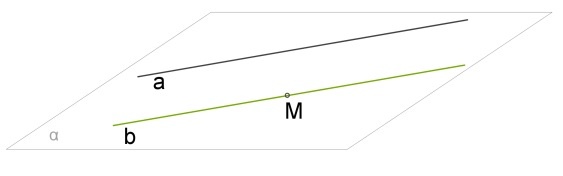
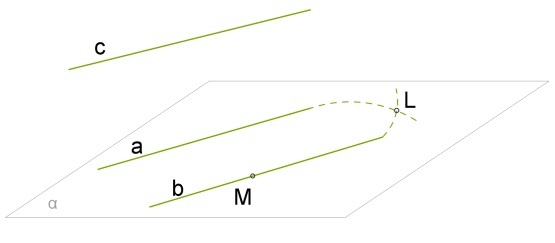
1. Есть a (прямая) и М (точка, далее — т.). Она не принадлежит a. Через них проходит плоскость альфа (\(\alpha\)). Известно, она единственная.Прямая b проходит через т.М и \(\vert\vert\;\) а. Она существует, что доказывает аксиома о \(\;\vert\vert.\)
2. Предположим, что существует прямая с, которая тоже проходит через т.М, причем c \(\vert\vert\) a. В этом случае потребуется другая плоскость \(\beta\), такая, чтобы прошла через т.М. Такое невозможно, потому что есть теорема, которая говорит, что плоскость только одна. Значит это одна и та же плоскость (\(\alpha\) совпала с \(\beta\)) и одна и та же прямая (b совпал с c). Единственность прямой доказана.

Теорема доказана.

Уравнение параллельной прямой

Если известно, что прямая проходит через какую-то точку с координатами и параллельна другой прямой y=kx+a, то ее уравнение можно найти по формуле:

\(\gamma-\gamma_0=\kappa\left(\chi-\chi_0\right)\)

где k —  угловой коэффициент.