Первообразная функции

Что такое первообразная функции

К примеру, требуется преобразовать производную, которая имеет следующий вид:

\(f(x)=x^{3}\)

Известна справедливая формула:

\(f(n)^{,}=n*x^{n-1}\)

Таким образом, можно посчитать заданную производную:

\(f^{,}(x)=(x^{3})^{,}=3x^{2}\)

Можно выполнить следующие подробные преобразования для \(x^{2}\)

\(x^{2}=\frac{(x^{3})^{,}}{3}\)

Исходя из формулировки производной, выражение можно представить и в таком виде:

\(x^{2}=(\frac{x^{3}}{3})^{,}\)

Таким образом, данная запись является определением первообразной. Для корректной записи следует выполнить следующую операцию:

\(x^{2}=\rightarrow \frac{x^{3}}{3}\)

По аналогии можно записать следующее выражение:

\(x^{4}=\rightarrow \frac{x^{5}}{5}\)

При обобщении этого правила, получится формула:

\(x^{n}=\rightarrow \frac{x^{n+1}}{n+1}\)

Выполнив необходимые действия, можно сформулировать определение первообразной.

Основное свойство, сколько первообразных существует для функции

Графически все подобные первообразные данной функции f(х) получают из геометрического графика какой-то одной первообразной с помощью параллельных переносов по порядку вдоль оси Оу.

Первообразная функции и неопределенный интеграл

Обозначение неопределенного интеграла:

\(\int f(x)dx=F(x)+C\)

Где f(x) представляет собой подынтегральную функцию; f(x) dx —подынтегральное выражение; x представляет собой переменную интегрирования; F(x) является одной из первообразных функции f(x); С является элементарной произвольной постоянной.

Существует несколько характерных для интеграла свойств:

1. Производная неопределённого интеграла представляет собой подынтегральную функцию вида \((\int f(x)dx)^{,}=f(x)\).
2. Постоянный множитель, используемый в подынтегральном выражении, допускается выносить за знак интеграла \(\int k*f(x)dx=k*\int f(x)dx\).
3. Интеграл от суммы или разности функций представляет собой сумму или разность интегралов от этих функций \(\int (f(x)\pm g(x))dx=\int f(x)dx\pm \int g(x)dx\).
4. Когда k и b являются постоянными, при этом k не равно нулю, то \(\int f(kx+b)dx=\frac{1}{k}*F(kx+b)+C\).

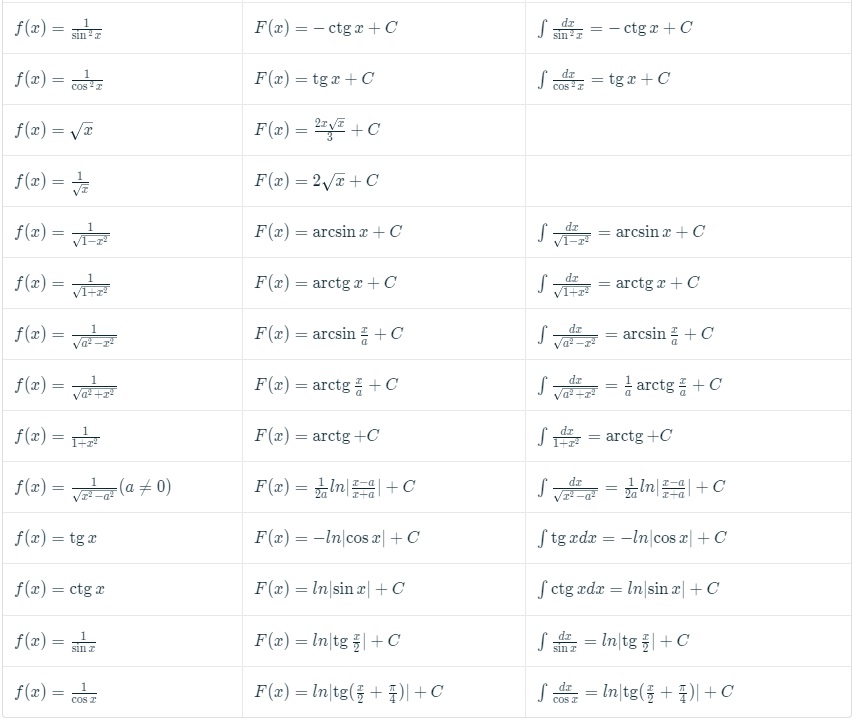
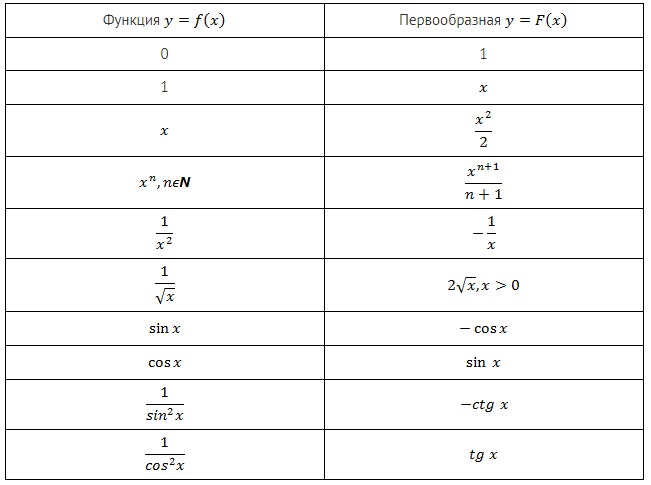
Таблица первообразных с неопределенными интегралами будет иметь следующий вид:

Допустим, что дана функция f(х), F является ее произвольной первообразной. В процессе расчетов можно записать следующее выражение для решения:

\(\int_{a}^{b}{f(x)dx}=F(x)\mid \frac{b}{a}=F(b)-F(a)\)

Где F(x) представляет собой первообразную для f(x).

Таким образом, интеграл функции f(х) на физическом промежутке (а;b) представляет собой разность первообразных в точках b и а.

Как записать всю совокупность первообразных функций

Совокупностью всех первообразных функций F(х) + С функции f (х) на определенном промежутке называют неопределенным интегралом и обозначают с помощью символа \(\int\).

Элементарная запись выглядит следующим образом:

\(\int f(x)dx=F(x)+C\)

Где f (x) dx является подынтегральным выражением; f (x) представляет собой подынтегральную функцию; х — это переменная интегрирования; F (x) представляет собой первообразную для функции f (x); С — является некоторой постоянной величиной.

d является знаком дифференциала и обладает двойным назначением:

• отделяет подынтегральную функцию от переменной интегрирования;
• все, что стоит после этого знака, дифференцируется по умолчанию и умножается на подынтегральную функцию.

Таблица первообразных и правила их нахождения

В качестве разъяснения можно использовать пример первообразной:

\(F(x)=\frac{7x^{2}}{2}\)

Данная первообразная для функции:

f(х) = 7х

В качестве подтверждения следует представить производную:

\((\frac{7x^{2}}{2})^{,}=7x\)

\(F^{,}(x)=f(x)\)

К примеру, необходимо решить пару задач:

1. Прямая задача заключается в дифференцировании, при данной функции F(х) требуется найти \(F^{,}(x)\).
2. Вторая задача является обратной, при данной функции f(x) в виде производной неизвестной функции F(х) требуется найти F(х) — первообразную.

Нахождение F(х) выполняют двумя способами:

• таблица первообразных;
• правила поиска первообразных.

Таблица первообразных

Можно выполнить проверку:

\((\frac{x^{2}}{2})^{,}=2*\frac{1}{2}x=x\)

\((2\sqrt{x})^{,}=2*\frac{1}{2\sqrt{x}}=\frac{1}{\sqrt{x}}\)

\((tg x)^{,}=\frac{1}{\cos ^{2}x}\)

С помощью простых вычислений можно проверить все строчки таблицы. Таким образом, будет выполняться соотношение:

\(F^{,}(x)=f(x)\)

С помощью специальных правил можно отыскать первообразные. Согласно первому правилу, первообразная суммы равна сумме первообразных. Допустим:

\(F^{,}(x)=f(x)\)

F является первообразной для f.

\(G^{,}(x)=g(x)\)

G является первообразной для g.

Необходимо представить доказательство выражения:

F + G является первообразной для f + g.

Доказательство:

\((F+G)^{,}= (F)^{,}+ (G)^{,}=f+g\)

Второе правило о постоянном множителе. По условиям задачи:

\(F^{,}(x)=f(x)\)

Где F представляет собой первообразную для f; k является константой.

Требуется подтвердить, что:

kF является первообразной для kf.

Доказательство:

Доказать данное выражение можно с помощью определения первообразной и по правилу дифференцирования. Таким образом:

\((kF)^{,}= k(F)^{,}=kf\)

Смысл правила заключается в том, что при известной первообразной для f можно получить первообразную для kf с помощью умножения F на k.

Третье правило можно записать таким образом:

если y = F(x) является первообразной для функции y = f(x),

то \(y=\frac{1}{k}F(kx+m)\) представляет собой первообразную для \(y=f(kx+m)\).

Допустим, что:

\(F^{,}(x)=f\)

Требуется доказать:

\((\frac{1}{k}F(kx+m)) ^{,}= f(kx+m)\)

Доказательство:

\((\frac{1}{k}F(kx+m)) ^{,}= \frac{1}{k}F^{,} (kx+m)k= F^{,} (kx+m)=f(kx+m)\).