Как найти периметр квадрата
Что такое периметр квадрата
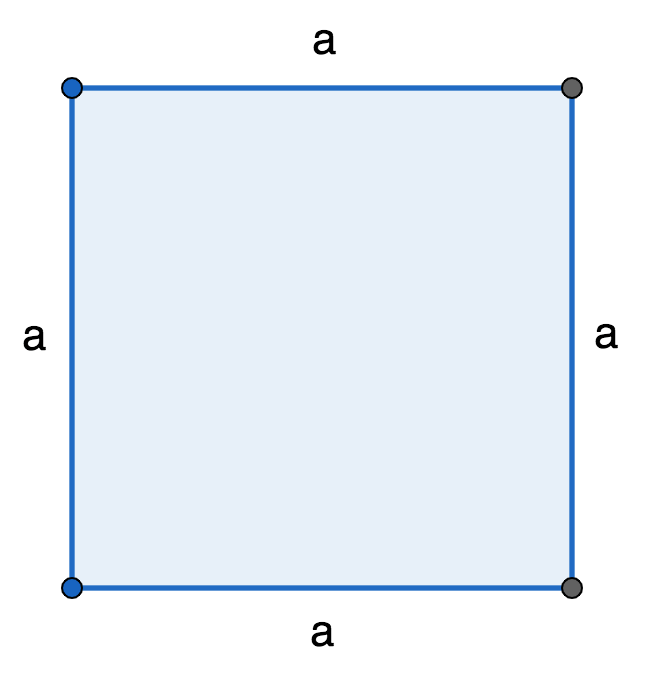
Квадрат — это правильный четырехугольник, все его стороны и углы равны.
Про него также говорят, что это частный случай прямоугольника или ромба.
Периметр квадрата - это сумма длин всех его сторон или произведение одной его стороны на 4.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Способы вычисления
Для вычисления периметра квадрата применяется несколько видов несложных формул.
По длине стороны
Самый простой способ, если известна величина одной из его сторон. Сразу вспоминаем, что мы имеем дело с правильным четырехугольником, и подставляем значение в уравнение:
\(P\;=\;4\times a\,\)
где \(a\) — это сторона фигуры.
По длине диагонали
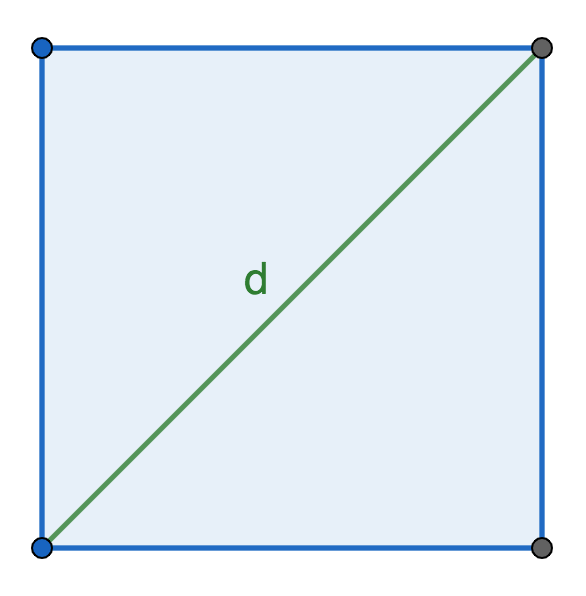
Если известна только диагональ правильного прямоугольника, формула для нахождения суммы всех его ребер будет выглядеть так:
\(P\;=\;2d\sqrt2\,\)
что следует из соотношения длин стороны и диагонали \(d=a\sqrt2\)
По площади
Зная площадь фигуры, найти ее периметр можно так:
\(P\;=\;4\sqrt S\\\)
По радиусу описанной окружности
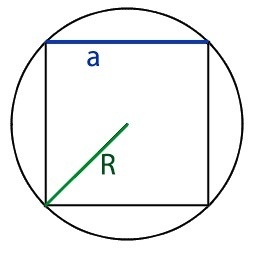
Радиус описанной вокруг квадрата окружности — это половина его диагонали. Формула для нахождения P в данном случае:
\(P\;=\;4R\sqrt2\,\)
где R — радиус данной окружности.
По радиусу вписанной окружности
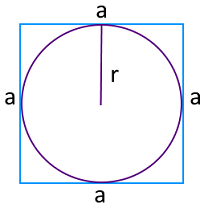
Радиус вписанной окружности — это половина величины ребра правильного прямоугольника. Таким образом, уравнение для нахождения P выглядит так:
\(P\;=\;8r\,\)
где r — радиус вписанной окружности.
Найти P квадрата, если его ребро a равно 5 см.
Решение:
Так как P = 4a, подставляем сюда известное значение, и получается \(P = 4\times5= 20\ см.\)
Ответ: 20 см.
Узнать P правильного четырехугольника, если его диагональ d равна 6 см.
Решение:
Используем формулу \(P\;=\;2d\sqrt2\) и подставляем известное значение. Получается: \(P = 2 * 6\sqrt2\ = 12\sqrt2\ см.\)
Ответ: \(12\sqrt2\ см.\)
Площадь квадрата равна 16 см². Каков периметр?
Решение:
Мы знаем, что \(P\;=\;4\sqrt S\\\). Значит, подставляя значение в формулу \(P\;=\;4\sqrt S\\\), мы имеем: \(P\;=\;4\sqrt 16\ = 4\times4\ = 16\) см.
Ответ: 16 см.
Задача 4
Известно, что 1/2 диагонали правильного прямоугольника составляет \(9\sqrt2\\ \)см. Вычислить P.
Решение:
1/2 диагонали имеющейся фигуры — это как раз радиус описанной окружности. Подставляем значение в уравнение \(P\;=\;4R\sqrt2\\\). Получается: \(P\;=\;4R\sqrt2\ = 4\times9\sqrt2\times\sqrt2\ = 72\) см.
Ответ: 72 см.
Дан квадрат и вписанная в него окружность. Половина стороны a фигуры равна 7 см, посчитать P.
Решение:
Так как половина стороны данной фигуры — это радиус вписанной в нее окружности. Используем метод нахождения по радиусу вписанной окружности: \(P\;=\;8r\\\). Подставляем известное значение: \(P\;=\;8r\ = 8\times7\ = 56\ см.\)
Ответ: 56 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так