Формула расчета периметра многоугольника

Что такое периметр многоугольника

Свойства многоугольника

1. Все стороны прямые.
2. Стороны не пересекаются (кроме звездчатых).
3. Двумерная фигура.
4. Сумма внешних углов всегда равна 360º.
5. Сумма внутренних углов равна \(\frac{n(n-3)}2\) (для правильных фигур).

Как вычислить периметр правильного многоугольника

Свойства правильного многоугольника

1. Все стороны равны.
2. Все углы равны.
3. Центр равно удален ото всех вершин и сторон.
4. Сумма всех углов равна 180º×(n−2).
5. Все внешние углы при сложении их градусных мер дадут 360º.
6. Все биссектрисы углов между сторонами равны и пересекают центр фигуры.
7. Возможно вписать окружность и описать круг. Площадь кольца зависит от длины стороны многоугольника.

Формула

P=a×n

где a — длина стороны, n — количество сторон.

Для неправильного многоугольника

Описание

У неправильного многоугольника все стороны разного размера.

Формула

Его периметр (P) можно рассчитать, сложив все длины его сторон (a, b, c,d и т.д.). Это первый способ.

 P=a+b+c+d+...

Второй способ: если есть стороны с одинаковыми длинами, формулу можно сократить, использовав умножение.

По заданным координатам

Как начертить многоугольник

Еще один способ вычисления периметра многоугольника - построить фигуру на координатной прямой.

Для этого нужно:

1. Построить координатные оси.
2. Нанести на них заданные координаты (длины) сторон. Соединить точки.

Формула для расчета периметра

Далее нужно находить длины всех получившихся сторон. 

1. Размеры прямых сторон легко узнавать методом подсчета координатных меток между точками сторон. Записать получившиеся значения рядом со сторонами.
2. Найти длину наклонных сторон. Это можно сделать по формуле: \(d=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

    3. Найти периметр сложением длин всех сторон по формуле для неправильного многоугольника: P=a+b+c+d..., где a,b,c,d... — длины сторон. А если получился правильный:      P=a×n, где a - длина стороны, а n - количество сторон фигуры.

Примеры решения задач

Пример 1

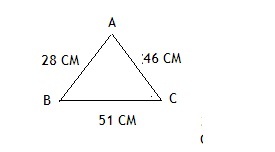
Дан треугольник ABC. AB=28см, BC=51см, AC=46см. 

Решение

P=AB+BC+AC=28+51+46=125см

Пример 2

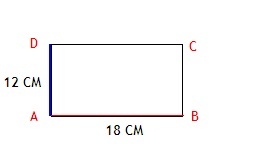
В прямоугольнике ABCD длина синей стороны 12 см, а красной 18 см.

Решение

AD=BC=12см 

AB=CD=18см.

P=12×2+18×2=24+36=60см.

Пример 3

Дан квадрат со стороной 12 см.

Решение

Мы знаем, что все стороны квадрата одинаковые. Их всего 4. Значит, P=12×4=48см.

Пример 4

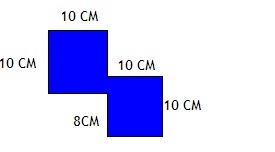
Дана фигура (данные на рисунке).

Решение

На рисунке мы видим восьмиугольник. У него шесть сторон по 10 см и две стороны по 8 см. Значит, P=10×6+8×2=60+16+76см.