Формула нахождения периметра параллелограмма
Что такое периметр параллелограмма
Периметр параллелограмма — это сумма длин всех его сторон.
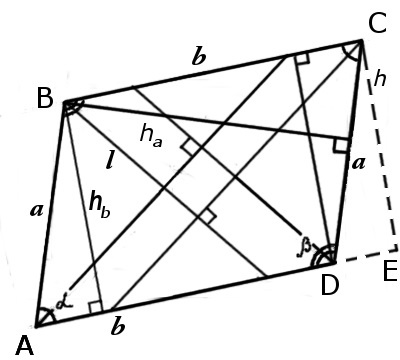
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно равны и параллельны друг другу. Таким образом, его периметр — это удвоенная сумма двух его смежных ребер.
Свойства
- противоположные стороны равны и параллельны;
- противоположные углы попарно равны;
- сумма соседних углов равна 180 градусов;
- сумма всех углов равна 360 градусов;
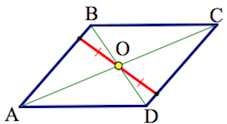
- диагонали фигуры делятся пополам в точке пересечения;
- точка пересечения диагоналей — центр симметрии параллелограмма;
- биссектриса образует равнобедренный треугольник.
Как найти периметр
Существует несколько основных способов, с помощью которых можно найти сумму длин всех сторон заданной фигуры. Все они зависят от изначально известных параметров.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
По сумме всех сторон
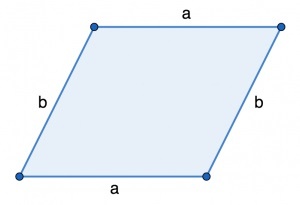
Так как периметр параллелограмма — это удвоенная сумма двух его смежных ребер, используем формулу:
P=2(a+b),
где a и b — это две смежные стороны данного четырехугольника.
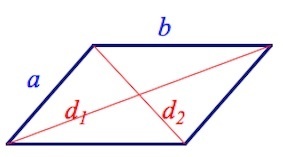
По стороне и двум диагоналям
Если в задаче дана лишь одна сторона, но обе диагонали четырехугольника, мы можем найти вторую сторону. Для этого используем формулу:
\(a=\frac{\sqrt{2d_1^2+2d_2^2-4b^2}}2,\)
где \(d_1\) и \(d_2\) — это обе диагонали фигуры.
Получается, что расчет суммы длин всех сторон для параллелограмма будет выглядеть так:
\(P=2(\frac{\sqrt{2d_1^2+2d_2^2-4b^2}}2+b).\)
По стороне, высоте и синусу угла
В случае, если нам известны лишь одно ребро, высота и один из углов, можем узнать длину второго ребра таким образом:
\(a=\frac{h_b}{\sin\alpha}\)
где \(h_b\) — высота, проведенная к известной стороне, а \(sin\alpha\) — известный нам угол.
Таким образом, формула для нахождения периметра параллелограмма будет выглядеть так:
\(P=2(\frac{h_b}{\sin\alpha}+b)\)
Примеры решения задач
Попробуем применить полученные знания на практике и рассмотрим несколько задач на периметр параллелограмма.
Задача 1
Дан параллелограмм со сторонами 5 см и 9 см. Вычислить его периметр.
Решение:
Воспользуемся формулой P=2(a+b), так как нам известны обе стороны фигуры. Подставляем значения: P=2(5+9)=28 см.
Ответ: 28 см.
Задача 2
Известно, что одна из сторон параллелограмма равна 4 см, а две его диагонали равны 6 см и 8 см. Найти периметр фигуры.
Решение:
Для расчета суммы длин всех сторон используем формулу:
\(P=2(\frac{\sqrt{2d_1^2+2d_2^2-4b^2}}2+b)\)
Подставляем известные значения:
\(P=2(\frac{\sqrt{2d_1^2+2d_2^2-4b^2}}2+b)=2(\frac{\sqrt{2\times6^2+2\times8^2-4\times4^2}}2+4)=2(\frac{\sqrt{72+128-64}}2+4)=2(\frac{2\sqrt{34}}2+4)=2\sqrt{34}+8\) см.
Ответ:\( 2\sqrt{34}+8\) см.
Задача 3
Сторона b параллелограмма равна 2 см, высота, проведенная к b — 1 см, а угол α равен \(\frac\pi6\). Найти сумму длин всех сторон фигуры.
Решение:
Для расчета будем использовать уравнение:
\(P=2(\frac{h_b}{\sin\alpha}+b)\)
Подставим известные величины:
\(P=2(\frac1{\sin{\displaystyle\frac\pi6}}+2)=2(\frac1{\displaystyle\frac12}+2)=8\;\)см.
Ответ: 8 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так