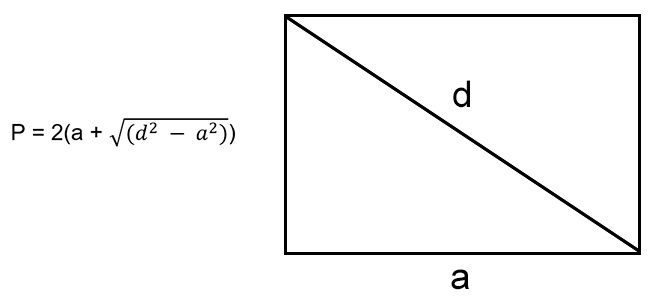Как найти периметр прямоугольника

Периметр прямоугольника

Основные свойства прямоугольника:

• противоположные стороны фигуры равны и параллельны друг другу;
• сумма всех углов равна 360 градусов;
• диагонали прямоугольника равны по длине и точкой пересечения делятся пополам;
• диагонали делят фигуру на два одинаковых прямоугольных треугольника;
• по теореме Пифагора, квадрат диагонали прямоугольника равен сумме квадратов двух его соседних ребер;
• стороны рассматриваемого четырехугольника также являются его высотами;
• точка пересечения диагоналей — это центр прямоугольника и также центр вписанной окружности;
• диагональ этого четырехугольника — это диаметр описанной окружности;
• вокруг него всегда можно описать окружность.

Варианты нахождения периметра прямоугольника

По сторонам

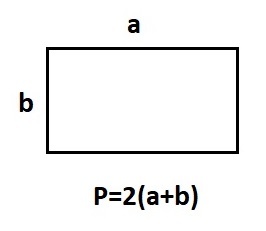
Если нам известны все стороны прямоугольника (или две смежные), мы можем использовать следующую формулу для нахождения суммы длин всех ребер:

\(P=2(a+b)\)

где \(a\) и \(b\) — это две соседние стороны фигуры.

По любой стороне и площади

Зная значение любого из ребер четырехугольника и его площадь, мы можем найти значение второго и периметр фигуры.

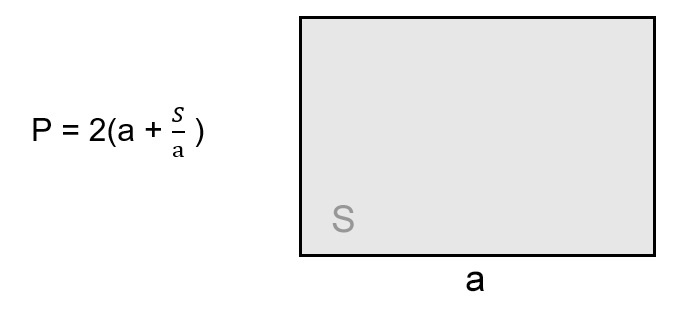
Так как площадь прямоугольника — это произведение двух его смежных сторон \((S=a\times b)\), чтобы найти неизвестную сторону, нужно поделить площадь на известную величину: \(b=\frac Sa\).

Получается, что формула для расчета \(P\) рассматриваемой фигуры будет выглядеть следующим образом:

\(P=2(\frac Sa+a)\)

По любой стороне и диагонали

В случае, если мы знаем длину одного из ребер и диагональ данного четырехугольника, мы можем найти вторую сторону с помощью теоремы Пифагора.

\(b=\sqrt{d^2-a^2}\)

где \(d\) — диагональ прямоугольника, а \(b\) — неизвестная сторона.

Чтобы рассчитать сумму длин всех сторон, нужно воспользоваться формулой:

\(P=2(a+\sqrt{d^2-a^2})\)

По любой стороне и радиусу описанной окружности

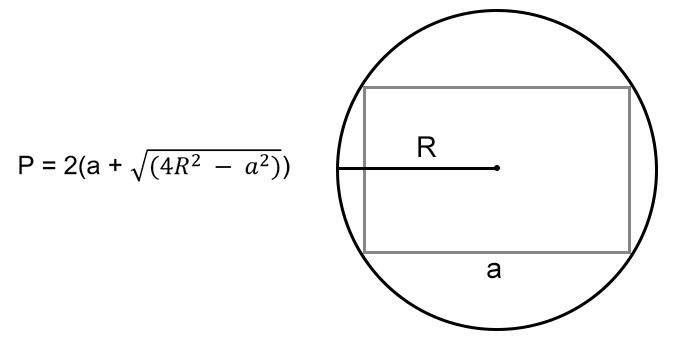
Когда нам известна одна из сторон и радиус описанной окружности вокруг прямоугольника, мы можем узнать его неизвестное ребро. Из свойств прямоугольника помним, что точка пересечения диагоналей фигуры — это центр описанной окружности. Это значит, что 1/2 диагонали — это радиус этой окружности. Таким образом, по теореме Пифагора мы можем узнать неизвестную сторону прямоугольника:

\(b=\sqrt{4R^2-a^2}\)

где \(R\) — радиус описанной окружности.

Тогда формула для расчета P будет выглядеть так:

\(P=2(a+\sqrt{4R^2-a^2})\)

Примеры решения задач

Задача 1

Известно, что стороны прямоугольника равны 5 см и 7 см. Найти его периметр.

Решение:

Применяем самую первую формулу для расчета:

\(P=2(a+b)\)

Получается:

\(P=2(5+7)=24\) см

Ответ: 24 см.

Задача 2

Мы знаем, что площадь четырехугольника с прямыми углами составляет 24 \(см^2\), одна из его сторон равна 6 см. Вычислить Р фигуры.

Решение:

Берем формулу \(P=2(\frac Sa+a)\) и подставляем известные значения:

\(P=2(\frac{24}6+6)=2\times10=20\) см

Ответ: 20 см.

Задача 3

Дан прямоугольник со стороной 3 см и диагональю 5 см. Нужно высчитать P данной фигуры.

Решение:

Вспоминаем формулу для расчета \(P=2(a+\sqrt{d^2-a^2})\) и вставляем известные величины:

\(P=2\;(3+\sqrt{5^2-3^2})=2(3+\sqrt{25-9})=2\times7=14\) см

Ответ: 14 см.

Задача 4

Вокруг прямоугольника с ребром 3 см описали окружность с радиусом 5 см. Определить P заданной фигуры.

Решение:

В этом случае для расчета суммы длин всех сторон применяем формулу \(P=2(a+\sqrt{4R^2-a^2})\). Используем известные значения и получаем:

\(P=2\;(3+\sqrt{4\times5^2-3^2})=2(3+\sqrt{100-9})=2(3+\sqrt{91})=6+2\sqrt{91}\) см.

Ответ: \(6+2\sqrt{91}\) см.