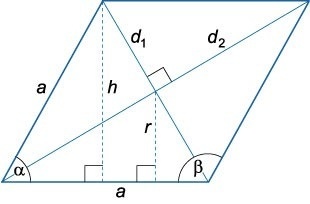
Формула нахождения периметра ромба
Периметр ромба
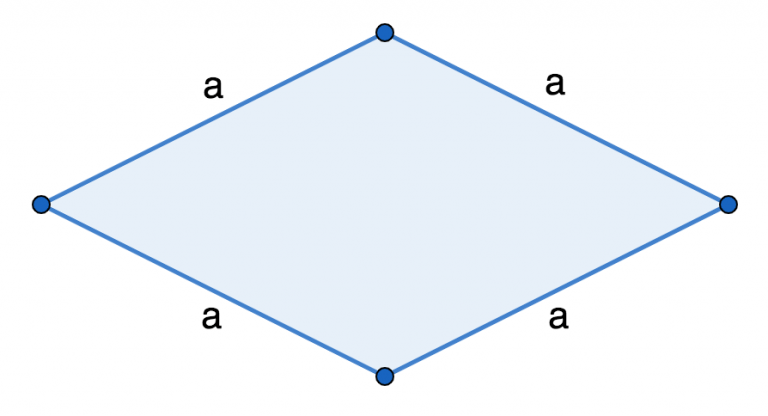
Ромб — это четырехугольник с равными сторонами.
Также его называют параллелограммом, у которого все ребра равны. При этом его противоположные углы тоже равны между собой. Если все углы равны 90 градусов, то это квадрат.
Периметр ромба - сумма длин всего его сторон или произведение любой его стороны на 4.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Способы нахождения
Рассмотрим все способы нахождения периметра этой фигуры.
По сторонам
Если нам известны величины одного из его ребер, мы без проблем можем найти P по формуле:
\(P\;=\;a+a+a+a\;=\;4\times a,\)
где a — это сторона ромба.
По двум диагоналям
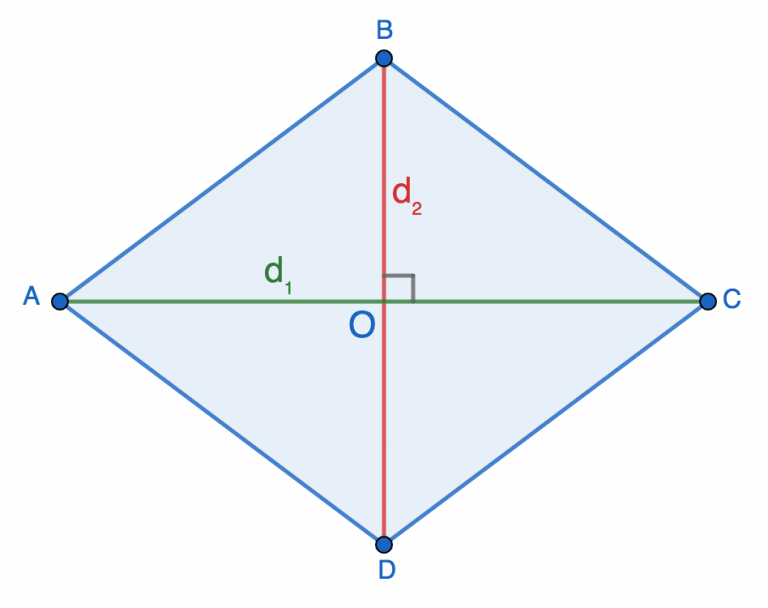
Если наш ромб — не квадрат, то две его диагонали будут не равны между собой. Также в любом ромбе они пересекаются под углом 90 градусов, а в точке пересечения делятся пополам. Если обе из них нам известны, то можем вычислить периметр фигуры следующим образом:
\(P=4\times\sqrt{\left(d_1/2\right)^2+\left(d_2/2\right)^2},\)
где \(d_1\) и \(d_2\) — это диагонали четырехугольника.
Подобные вычисления получились исходя из свойств диагоналей равностороннего четырехугольника. Вместе со сторонами фигуры они образуют прямоугольный треугольник. По теореме Пифагора:
\(a^2=\left(d_1/2\right)^2+\left(d_2/2\right)^2\)
\(a=\sqrt{\left(d_1/2\right)^2+\left(d_2/2\right)^2}.\)
По диагонали и углу
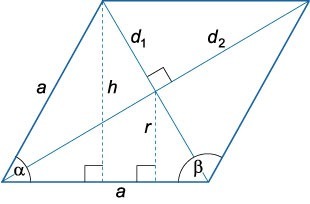
Чтобы вычислить сумму всех ребер ромба данным способом, для начала нужно определить величину одной стороны:
- если нам известен острый угол α: \(a=\frac{d_1}{\sqrt{2+2\cos\alpha}};\)
- если известен тупой угол \(β: a=\frac{d_2}{\sqrt{2-2\cos\beta}}.\)
Далее расчет P будет выглядеть следующим образом:
- \(P=\frac{4d_1}{\sqrt{2+2\cos\alpha}}\);
- \(P=\frac{4d_2}{\sqrt{2-2\cos\beta}}.\)
По площади и радиусу вписанной окружности
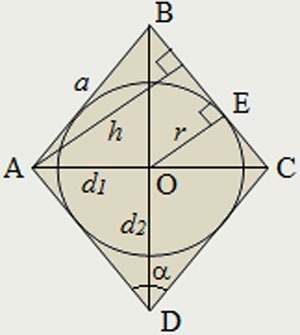
По известной площади и радиусу вписанной окружности можно находить P, опираясь на формулу:
\(P=\frac{2S}r,\)
где r — это радиус вписанной окружности.
По площади и синусу одного из углов
В этом случае формула расчета суммы всех сторон выглядит так:
\(P=4\times\frac{\sqrt S}{\sqrt{\sin\alpha}},\) либо
\(P=4\times\frac{\sqrt S}{\sqrt{\sin\beta}}.\)
Через большую диагональ и половинный угол
\(P=\frac{2d_1}{\sqrt{\cos(\alpha/2)}}\) или
\(P=\frac{2d_1}{\sqrt{\sin(\beta/2)}}.\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так