Как найти периметр трапеции

Основные свойства трапеции

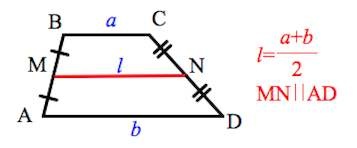
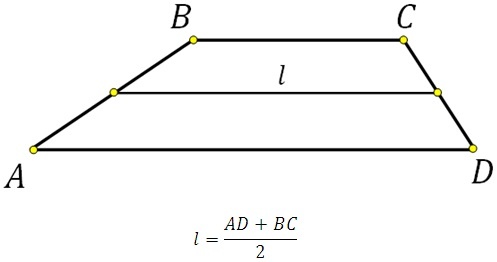
• средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;

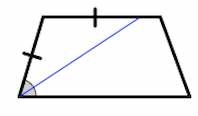
• биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;

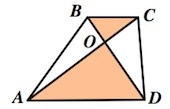
• треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;

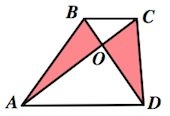
• треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;

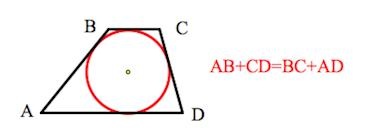
• если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;

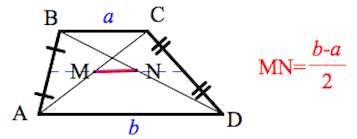
• точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;

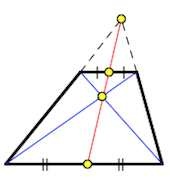
• середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;

Свойства равнобедренной трапеции

• в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
• диагонали равны;
• равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
• если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.

Способы нахождений периметра

Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.

По всем сторонам

Формула для нахождения периметра выглядит так:

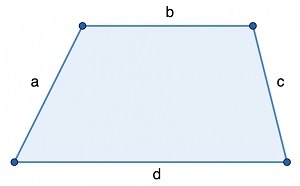
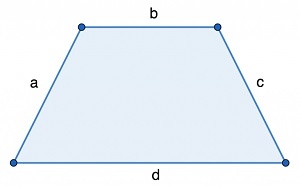
P=a+b+c+d

где a, b, c, d — стороны трапеции.

По сторонам равнобедренной трапеции

Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:

\(P=2\times a+b+c\)

или

\(P=2\times c+a+b\)

Через среднюю линию

Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:

\(P=2\times l+AB+CD\)

где l — средняя линия фигуры.

Примеры решения задач

Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.

Задача 1

Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.

Решение:

Нам пригодится самая первая формула для расчета:

P=a+b+c+d.

Подставляем значения и получаем:

P=4+7+5+10=26\;см.

Ответ: 26 см.

Задача 2

Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.

Решение:

Так как трапеция равнобедренная, удобнее всего будет использовать формулу:

\(P=2\times a+b+c\)

Таким образом, получается:

\(P=2\times 7+5+8=27\) см.

Ответ: 27 см.

Задача 3

Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.

Решение:

Считать будем по формуле

\(P=2\times l+a+c\)

\(P=2\times 6+5+9=26\) см.

Ответ: 26 см.