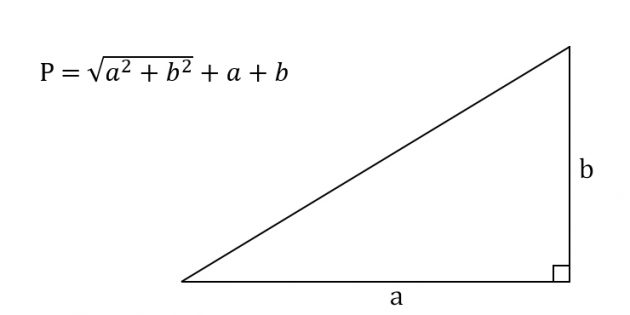Как найти периметр треугольника

Учимся находить периметр треугольника разными способами, а также тренируем полученные знания на примерах задач.

Периметр треугольника

Рассмотрим несколько способов нахождения периметра рассматриваемой фигуры. Каждая из предложенных формул опирается на те величины, которые нам уже известны.

Способы нахождения

По трем сторонам

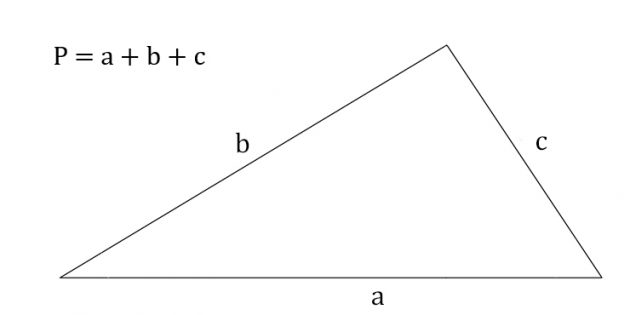
Если мы уже знаем длину каждого ребра фигуры, расчет периметра будет проходить так:

\(P = a+b+c\)

где a, b и с — это стороны треугольника.

В случае, если нам известны стороны равнобедренного треугольника (у которого два ребра равны), формула для расчета периметра выглядит следующим образом:

\(P=a+2b\) или \(P=a+2c \)

где a — основание фигуры, а b и с — равные ребра.

Треугольник может также быть равносторонним (когда все стороны равны). Тогда P будем находить в соответствии с расчетами:

\(P=3a\)

где a — это любая сторона фигуры.

По площади и радиусу вписанной окружности

Когда нам известна площадь данного многоугольника и радиус вписанной в него окружности, расчет P выглядит так:

\(P=\frac{2S}r\)

где S — площадь фигуры, r — радиус вписанной в нее окружности.

По двум сторонам и углу между ними

Так как нам известен угол и две стороны, которыми он образован, мы можем найти третью сторону треугольника по теореме косинусов. И потом уже вычислить сумму длин всех ребер фигуры.

Теорема косинусов выглядит так:

\(a^2=b^2+c^2-2bc\times\cos\alpha\)

где α — известный угол.

Тогда формула для расчета периметра всей фигуры в этом случае:

\(P=\sqrt{b^2+c^2-2bc\times\cos\alpha}+b+c\)

По боковой стороне и высоте (для равнобедренного)

Возвращаясь к свойствам равнобедренного треугольника, вспоминаем, что высота, проведенная к основанию треугольника из противоположной вершины, является одновременно высотой, биссектрисой и медианой. Это значит, что оба прямоугольных треугольника, которые она образует, равны между собой.

Формула для поиска периметра нашего равнобедренного будет опираться на теорему Пифагора. Пусть 1/2 основания (с) = d. Тогда:

\(d^2=a^2-h^2\)

\(d=\sqrt{a^2-h^2}\)

где a — сторона равнобедренного треугольника и гипотенуза прямоугольного, h — высота равнобедренного и катет прямоугольного.

Не забываем, что d — это лишь половина основания равнобедренного треугольника, поэтому для поиска периметра результат нужно будет умножить на 2.

\(P=2\sqrt{a^2-h^2}+2a\)

По двум катетам (для прямоугольного)

Еще раз вспомним теорему Пифагора для нахождения гипотенузы (обозначим ее буквой с).

\(c^2=a^2+b^2\)

\(c=\sqrt{a^2+b^2}\)

где a и b — катеты треугольника.

Подставляем значение c в формулу для нахождения периметра и получаем:

\(P=\sqrt{a^2+b^2}+a+b\)

Примеры решения задач

Для тренировки полученных знаний, рассмотрим несколько примеров решения задач на поиск периметра треугольника.

Задача №1

Какой P треугольника, если его стороны равны 6 см, 7 см и 3 см.

Решение:

Подставляем в формулу P = a+b+c известные величины и получаем: P = 6+7+3=16 см.

Ответ: 16 см.

Задача №2

Известно, что основание равнобедренного треугольника равно 6 см, а его боковая сторона — 4 см. Найти P фигуры.

Решение:

Для данного случая подходит формула P=a+2b, подствляем значения: \(P=6+4\times2 = 14\) см.

Ответ: 14 см.

Задача №3

Нам известно, что площадь треугольника — 24 см², а радиус вписанной в него окружности — 8 см. Найти P.

Решение:

В данном случае рассчитывать P будем следующим образом: \(P=\frac{2S}r\). С уже известными нам величинами получаем: \(P=\frac{2\times24}8 = 6\) см.

Ответ: 6 см.

Задача №4

Дан равнобедренный треугольник. Нам известна его боковая сторона (4 см) и высота, опущенная к основанию (2 см). Нужно вычислить периметр фигуры.

Решение:

Мы знаем, что в этом случае P вычисляется, как \(P=2\sqrt{a^2-h^2}+2a\). С имеющимися значениями получается: \(P=2\sqrt{4^2-2^2}+2\times2 = 4\sqrt3+4\) см.

Ответ: P=4\sqrt3+4 см.

Задача №5

Дан прямоугольный треугольник с катетами 5 см и 7 см. Определить периметр фигуры.

Решение:

В формулу \(P=\sqrt{a^2+b^2}+a+b\) подставляем известные значения: \(P=\sqrt{5^2+7^2}+5+7 = \sqrt{74}+12\) см.

Ответ: \(P=\sqrt{74}+12\) см.