Плотность распределения случайной величины

Содержание:

Содержание

Что такое плотность вероятности

Плотность вероятности — это производная от функции F(x), описывающей распределение случайной величины.

Двумерная, трехмерная, N-мерная плотность, иначе называемая совместной, определяет одновременное выполнение двух и более условий. Чтобы проанализировать взаимосвязь между характеристиками одного процесса, сдвинутыми на определенный интервал времени, или результаты одновременного броска двух игральных костей, нужно рассматривать двумерную плотность вероятности. Функция в таком случае должна определять одновременное выполнение двух условий: случайные величины \(X\) и \(Y\) одновременно принимают значения из интервалов \(x_{1\;}\leq X\leq x_2\\\) и \(y_{1\;}\leq Y\leq y_2\\\).

Практические задачи, где требуется вычислить случайные величины, часто приходится решать в квантовой механике, например, рассчитывая коэффициенты отражения и прохождения квантовых частиц, движущихся в потенциальном поле. Также непрерывные случайные величины широко используют в генетике, ядерной физике.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Плотность \(f(x)\) аналогична таким понятиям, как плотность тока в теории электричества или плотность распределения масс на оси абсцисс.

Свойства плотности распределения

Плотность распределения обладает следующими свойствами:

Интеграл от плотности равен единице по всему пространству: \(\int_{-\infty}^\infty f(x)dx=1\). Выражение \(f(x)dx\) называют элементом вероятности.
Плотность распределения выполняется почти всюду, множество, на котором функция не будет выполнена, имеет меру ноль. Отрицательной плотность быть не может.
Вероятность попадания непрерывной случайной величины в промежуток \([a,b]\) равна определенному интегралу от ее плотности в пределах этого промежутка.

Функция распределения непрерывной случайной величины

Функцию распределения непрерывной случайной величины можно представить в виде формулы \(F(x)\;=\;P(X)\).

Любое дискретное распределение не является абсолютно непрерывным относительно меры Лебега, поэтому дискретные случайные величины не имеют плотности.

Согласно центральной предельной теореме теории вероятностей, чаще всего сумма множества случайных и слабо связанных друг с другом величин стремится к нормальному распределению. Если распределить группу людей на подгруппы по росту, большинство окажется среднего роста, то же самое будет с весом, коэффициентом интеллекта и многими другими параметрами.

Также встречаются следующие абсолютно непрерывные распределения:

равномерное на отрезке \([a,b]\);
хи-квадрат;
логнормальное;
многомерное нормальное;
экспоненциальное;
Вейбулла;
Коши;
Парето;
Стьюдента;
Фишера.

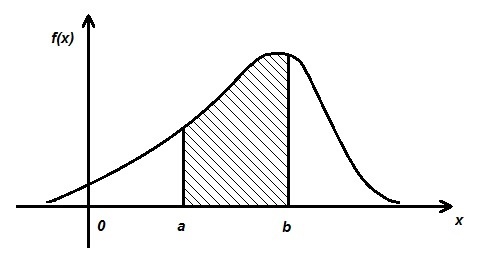
График плотности распределения

Площадь, заштрихованная на иллюстрации, соответствует вероятности события \(\{a\leq X\leq b\}.\)

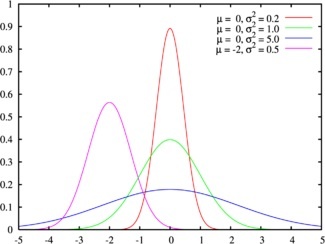
Нормальное распределение задается функцией плотности вероятности, совпадающей с функцией Гаусса.

\(\mu\) — математическое ожидание, \(\sigma\) — среднеквадратическое отклонение, \(а \sigma^2\) — дисперсия распределения.

Примеры задач

Задача 1

Распределение непрерывной случайной величины \(X\) задано функцией

\(F(x)\;=\;\left\{\begin{array}{lc}0,&x<-1\\\frac15(x+1),&c\leq x\leq d\\1,&x>4\end{array}\right.\)

Нужно найти значения \(с\) и \(d\), плотность распределения вероятностей \(f(x)\), построить графики функций \(F(x)\) и \(f(x)\).

Решение:

функция распределения непрерывна, следовательно:

\(F(c)\;=\;\frac15(c+1)\;=\;0\;\Rightarrow\;c\;=\;-1\)

\(F(d)\;=\;\frac15(d+1)\;=\;1\;\Rightarrow\;d\;=\;4\)

Таким образом:

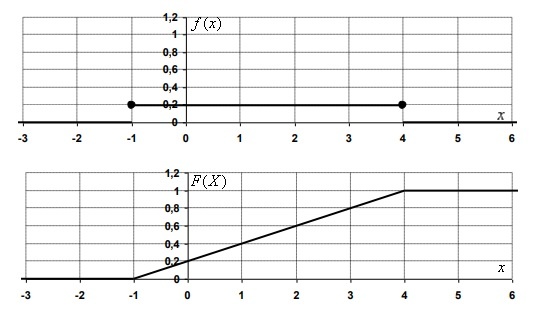
\(F(x)\;=\;\left\{\begin{array}{lc}0,&x<-1\\\frac15(x+1),&-1\leq x\leq4\\1,&x>4\end{array}\right.\)

\(f(x)\;=\;F'(x)\;=\;\left\{\begin{array}{lc}0,&x<-1\\\frac15,&-1\leq x\leq4\\1,&x>4\end{array}\right.\)

Задача 2

Написать функцию плотности нормального распределения случайной величины \(X\), если известно, что \(M(X) = 2\) и \(D(x) = 5.\)

Решение:

при распределении по нормальному закону функция имеет вид: \(f(x)\;=\;\frac1{\sigma\sqrt{2\pi}}e^\frac{{(x-a)}^2}{10}\), где \(a\) — математическое ожидание, \(\sigma\) — среднее квадратическое отклонение.

Подставим значения из условий задачи:

\(а = М(Х) = 2, \sigma\;=\;\sqrt{D(X)}\;=\;\sqrt5\)

Таким образом:

\(f(x)\;=\;\frac1{\sqrt{10\pi}}e^\frac{{(x-2)}^2}{10}\)

Насколько полезной была для вас статья?

Рейтинг: 3.00 (Голосов: 3)

Заметили ошибку?

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»