Как вычислить площадь квадрата

Квадрат

Нахождение площади квадрата

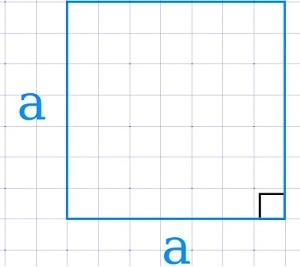
Через длину стороны

По аналогии с площадью прямоугольника можно вывести формулу:

\(S=a\cdot a=a^2\)

где а — сторона квадрата.

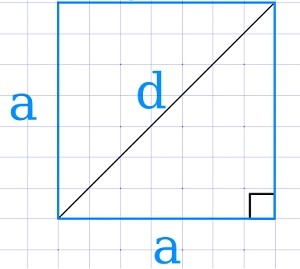
Через диагональ

\(S=\frac{d^2}2\)

где d — диагональ квадрата.

Также, стоит отметить, что в квадрате соотношение стороны и диагонали:

\(d=a\sqrt2\)

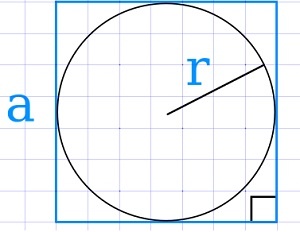
Через радиус вписанной окружности

\(S=4r^2\)

где r — радиус вписанной окружности.

Доказательство:

\(S=a^2=4\cdot(\frac{a^2}4)=4\cdot{(\frac a2)}^2=4\cdot r^2\)

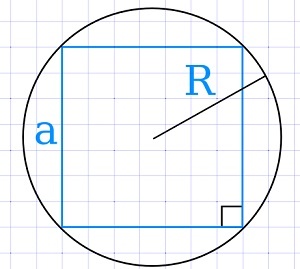
Через радиус описанной окружности

\(S=2R^2\)

где R — радиус описанной окружности.

Доказательство:

\(\left.\begin{array}{r}S=\frac{d^2}2\\R=\frac d2\end{array}\right\}S=2\cdot\frac{d^2}4=2\cdot{(\frac d2)}^2=2R^2\\\)

Через периметр

\(S=\frac{P^2}{16}\)

где Р — периметр квадрата.

Доказательство:

\(\left.\begin{array}{r}S=a^2\\P=4a\end{array}\right\}S=\frac{4a^2}4=\frac{16a^2}{16}=\frac{P^2}{16}\)