Построение треугольника по трем элементам
Построение треугольников
Треугольниками называют многоугольники с тремя сторонами и аналогичным количеством вершин.
При решении задач в рамках курса геометрии нередко приходится иметь дело с этими геометрическими фигурами. Прежде, чем приступать к вычислению составных элементов, необходимо научиться построению треугольников. Справиться с этим заданием несложно. Достаточно лишь правильно идентифицировать исходные данные и применить один из распространенных способов изображения фигур:
- по паре сторон и углу, который их разделяет;
- по определенной стороне и паре углов;
- на основании данных о трех сторонах.
Существует важная закономерность, которая существенно упрощает процесс построения геометрической фигуры с тремя сторонами и углами. Речь идет о сумме всех внутренних углов, из которых складывается рассматриваемый тип многоугольника, равной 180°. Перед изображением геометрической фигуры следует подготовить канцелярские принадлежности и инструменты:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- линейка;
- циркуль;
- карандаш.
Если следовать простому алгоритму действий, то можно легко избежать ошибок. Рекомендуется придерживаться следующей последовательности и воспроизводить геометрическую фигуру поэтапно:
- Анализ условия задания. В первую очередь стоит разобраться с задачей, выписать известные величины, выявить связь между данными и искомой геометрической фигурой. В результате получится спланировать дальнейшие действия.
- Изображение треугольника. Так как план готов, можно приступать к его реализации, используя подготовленные заранее инструменты.
- Доказательство. На этой стадии необходимо идентифицировать полученное изображение, руководствуясь основными признаками и терминологией.
- Исследование. Как и во многих математических и геометрических задачах, на заключительной стадии построения треугольника требуется проанализировать количество способов и возможности решения задачи.
По трем сторонам
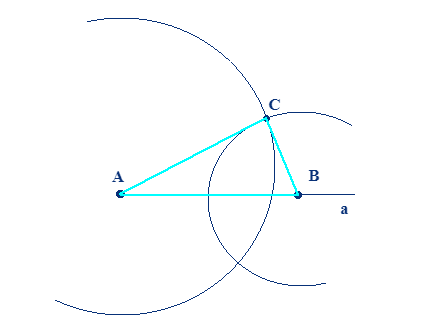
Представим, что известны значения трех сторон, из которых состоит треугольник. Пусть это будут стороны АВ, АС, ВС. Попробуем выполнить построение искомой геометрической фигуры, используя ранее рассмотренный алгоритм действий. Согласно обозначенной последовательности, необходимо в первую очередь проанализировать условия и спланировать работу по выполнению изображения. Порядок построения:
- провести прямую линию а с точками А и В;
- изобразить пару кругов с центрами в точках А и В;
- там, где окружности пересекаются, обозначить точку С;
- совместить с помощью прямых линий все три точки.
В результате получится треугольник АВС:
Перейдем к шагу с доказательством. Заметим, что на иллюстрации четко видно три стороны и аналогичное количество вершин изображенного многогранника. Таким образом, можно сделать вывод о построении треугольника, что и требовалось по условию задания.
Проанализируем полученную фигуру. Так как при наложении окружностей одна на другую получается лишь пара точек, в которых они пересекаются, при изображении второго подобного треугольника он совпадет с тем, что получился выше. Стоит отметить, что в треугольнике какая-либо из трех сторон всегда короче по сравнению с суммой двух других сторон. В противном случае построение многогранника с тремя сторонами и углами не представляется возможным, а у задания не будет решения.
По двум сторонам и углу
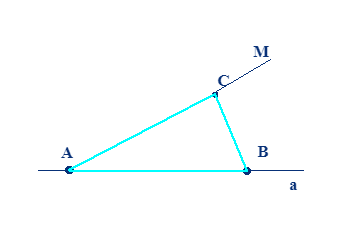
Рассмотрим другую ситуацию, когда известны величины двух сторон АВ и АС, а также угол \(\alpha\). Требуется выполнить построение треугольника. Как и в предыдущем случае, начать решение задачи стоит с анализа условий. Изучив предоставленную информацию, целесообразно спланировать дальнейшие действия:
- построить прямую линию а;
- обозначить на полученной прямой пару точек А и В;
- изобразить угол МАВ, величина которого идентична \(\alpha\);
- отмерить отрезок АС, который принадлежит прямой АМ;
- начертить третью сторону геометрической фигуры путем соединения точек В и С.
Наглядно результат реализации этого алгоритма выглядит следующим образом:
В процессе доказательства корректности представленного решения следует рассмотреть полученную геометрическую фигуру. Заметим, что все условия задачи соблюдены, а готовая фигура представляет собой треугольник. При исследовании рисунка становится понятно, что прямая линия а не имеет конца. Однако аналогичная линия совпадает с ней. Таким образом, данная задача обладает единственным решением при соблюдении условия о сумме внутренних углов. Если угол \(\alpha\) равен или больше, чем 180°, то задание невозможно решить.
По стороне и двум углам
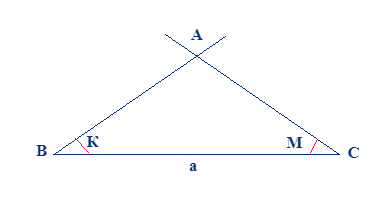
Еще один действенный способ изобразить многоугольник с тремя углами и тремя сторонами заключается в построении геометрической фигуры на основе информации о величине одной стороны и градусной мере пары углов, которые к этой стороне прилегают. Предположим, что известная сторона равна ВС, а углы соответствуют \(\alpha\) и \(\beta\).
Построим треугольник АВС с определенной стороной ВС, а также углами \(\angle К\) и \(\angle М\), равными \(\alpha и \beta\) соответственно. Тогда последовательность действий выглядит следующим образом:
- провести прямую линию а с точками В и С;
- из вершины В отложить \( \angle К\) на стороне ВС;
- из вершины С отложить \(\angle М\) на стороне ВС;
- точку, где пересекаются лучи изображенных углов, обозначить А;
- провести через точку А отрезки АС и АВ.
В результате получим геометрическую фигуру в виде многогранника с тремя сторонами и тремя углами:
Итогом построения является геометрическая фигура по всем признакам соответствующая треугольнику. Если расположить углы в другую сторону, то также получится построить искомый треугольник. С другой стороны, полученная фигура аналогична первой, поэтому задача имеет единственной решение. Важным требованием является выполнение правила о сумме внутренних углов.
Примеры решения задач
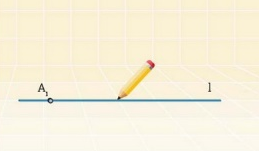
Известны величины трех отрезков АВ, ВС, СА. Необходимо построить треугольник А1В1С1.
Источник: resh.edu.ru
Решение
Отметим прямую линию l и точку А1.
Источник: resh.edu.ru
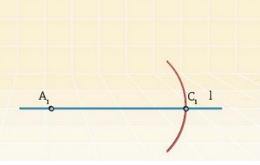
Отложим на полученной прямой А1С1:
Источник: resh.edu.ru
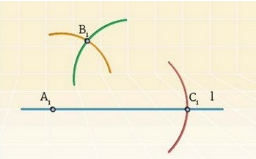
Отметим точку В1:
Источник: resh.edu.ru
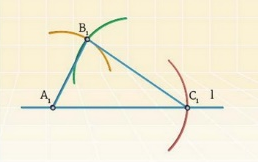
Соединим полученные точки, которые станут вершинами искомого треугольника.
Источник: resh.edu.ru
По результатам анализа полученного многогранника с тремя углами и тремя сторонами понятно, что изображенная геометрическая фигура является треугольником. Кроме того, у данной задачи имеется единственное решение.
Ответ: треугольник А1В1С1
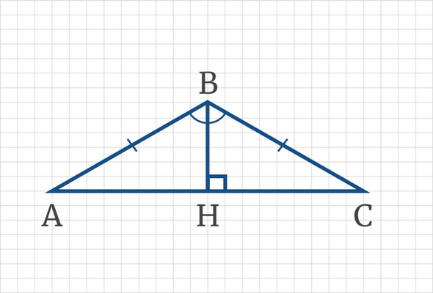
На рисунке представлен треугольник. Необходимо вычислить, насколько вершина В удалена от стороны АС. Известны следующие величины: АВ = ВС = 10 см \(\angle АВС = 120°\)
Источник: resh.edu.ru
Решение
Так как представленный на изображении треугольник является равнобедренным, то его высота аналогична биссектрисе. Кроме того, ВН соответствует расстоянию между точкой В и отрезком АС:
\(ВН \bot АС\)
\(\angle АВН = 120° \div 2 =60°\)
\(\angle А = 30°\)
Напротив вычисленного угла А расположен катет ВН, величина которого составляет по формуле ½ от величины гипотенузы. Таким образом:
\(ВН = 10 \div 2 = 5\)
Ответ: 5 см
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так