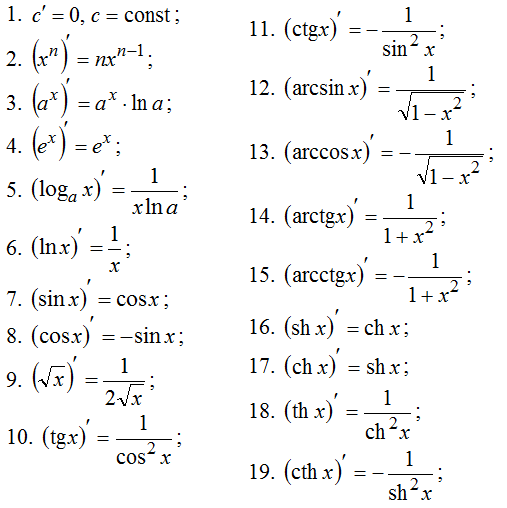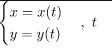Дифференцирование производных: по каким правилам осуществляется

Понятие производной — что это такое

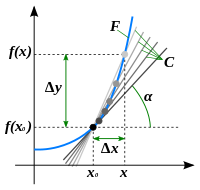
Производная функции представляет собой дифференциальное исчисление для определения скорости, с которой изменяется рассматриваемая функция.

Элементарный расчет производной заключается в определении предела отношения изменения функции к изменению ее аргумента при стремлении приращения аргумента к нулевому значению, если такой предел существует. Функция будет являться дифференцируемой в том случае, когда у нее есть конечная производная в определенной точке. Операции с функцией:

• дифференцирование заключается в определении производной функции;
• интегрирование является процессом, обратным дифференцированию, служит для расчета первообразной функции.

В физическом смысле производная определяется следующим образом: скорость материальной точки в момент времени \(t_{0}\) рассчитывается, как производная закона движения \(s(t_{0})\) рассматриваемой точки в определенный момент времени \(t_{0}: v(t_{0})=s^{,}(t_{0})\)

Основные правила дифференцирования

Производная первого порядка функции \(y=f(x)\) определяется с помощью таблицы производных. Она включает также формулы с использованием дроби, степени, корня, и имеет такой вид:

\((f (x) +g(x))^{,}=f^{,}(x)+g^{,}(x)\)

\((f (x)g(x))^{,}=f^{,}(x) g(x)+g^{,}(x) f (x)\)

\((\frac{f(x)}{g(x)})^{,}=\frac{f^{,}(x) g(x)-g^{,}(x) f (x)}{(g(x))^{2}}\)

В качестве доказательства теоремы необходимо выполнить ряд действий. Следует обозначить

\(\Delta f=f(x+\Delta x)+f(x)\)

\(\Delta g=g(x+\Delta x)+g(x)\)

Таким образом:

\(\frac{\Delta f}{\Delta x}\rightarrow f^{,}(x)\)

\(\frac{\Delta g}{\Delta x}\rightarrow g^{,}(x)\)

при стремлении \(\Delta x\) к нулю, так как есть \(f^{,}(x)\) и \(g^{,}(x)\)

Также отметим, что функции непрерывны в точке х, поэтому:

\(f(x+\Delta x)= \Delta f+f(x)\)

\(g(x+\Delta x)= \Delta g+g(x)\)

где \(f^{,}(x)\) и \(g^{,}(x)\) стремятся к нулю.

В том случае, когда \(y = f(x) +g (x)\), получим:

\(\Delta y= f(x+\Delta x)+ g(x+\Delta x)-f(x)- g(x)\)

Таким образом:

\(\frac{\Delta y}{\Delta x}=\frac{\Delta f}{\Delta x}+\frac{\Delta g}{\Delta x}\)

Правая часть уравнения при изменении х, стремящегося к нулю, обладает пределом, который равен:

\(f^{,}(x)+g^{,}(x)\)

Таким образом, имеет место предел левой части уравнения, который, исходя из определения, равен:

\((f(x)+g(x)) ^{,}\)

Данное выражение доказывает первую формулу.

При \(y=f (x)g(x)\) будет справедливо выражение:

\(\Delta y=f(x+\Delta x)g(x+\Delta x)-f(x)g(x)=(f(x)+\Delta f)(g(x)+\Delta g)-f(x)g(x)=f(x)\Delta g+g(x)\Delta f+\Delta f\Delta g\)

\(\frac{\Delta y}{\Delta x}=f(x)\frac{\Delta g}{\Delta x}+g(x)\frac{\Delta f}{\Delta x}+\frac{\Delta f}{\Delta x}\Delta g\)

Таким образом, получим уравнение:

\((f (x)g(x))^{,}=f^{,}(x) g(x)+g^{,}(x) f (x)\)

Так как:

\(\frac{\Delta g}{\Delta x}\rightarrow g'(x) \)

\(\frac{\Delta f}{\Delta x}\rightarrow f'(x) \)

\(\Delta g\rightarrow 0 при \Delta x\rightarrow 0\)

Представим, что \(y= \frac{f(x)}{g(x)} \) тогда:

\(\Delta y= \frac{f(x+\Delta x)}{g(x+\Delta x)}-\frac{f(x)}{g(x)}=\frac{f(x)+\Delta f}{g(x)+\Delta g}-\frac{f(x)}{g(x)} \)

или

\(x\Delta y=\frac{\Delta fg(x)-\Delta gf(x)}{g(x)g(x+\Delta x)} \)

Таким образом:

\(\frac{\Delta y}{\Delta x}=\left(\frac{\Delta f}{\Delta x}g(x)-\frac{\Delta g}{\Delta x}f(x)\right)\frac{1}{g(x+\Delta x)g(x)} \)

Переходя к пределу в этом равенстве, и учитывая, что \(g(x+\Delta x)\rightarrow g(x) \) при \(\Delta x\rightarrow 0\)

где \(g(x)\neq 0\)

Получим формулу \((\frac{f(x)}{g(x)})^{,}=\frac{f^{,}(x) g(x)-g^{,}(x) f (x)}{(g(x))^{2}}\)

Данная теорема имеет несколько следствий.

Если функция f дифференцируема в точке x и C является постоянной, тогда получим:

\((Cf(x))’=Cf'(x) \)

Таким образом, постоянный множитель можно выносить из-под знака дифференцирования.

Если функции \(f_{k}\ (k=\overline{1,n})\) дифференцируемы в точке x и \(C_k\) и \((k=\overline{1,n})\) являются постоянными, то

\(\left(\sum_{k=1}^{n}C_{k}f_{k}(x)\right)’=\sum_{k=1}^{n}C_{k}f_{k}(x)’ \)

Таким образом, производная линейной комбинации дифференцируемых функций равна такой же линейной комбинации производных данных функций.

Согласно теореме и понятию дифференциала можно сделать вывод, что:

\(d(f+g)=df+dg,\quad d(fg)=gdf+fdg\)

\(d\left(\frac{f}{g}\right)=\frac{gdf-fdg}{g^{2}}\)

\(\quad g\neq 0\)

В расчетах применяют правила дифференцирования или нахождения производных:

1. Константа может быть вынесена за знак производной: \((c*u(x))^{,}=c*(u(x))^{,}\)
2. Производная суммы или разности определяется таким образом: \((u\pm v)^{,}=u^{,}\pm v^{,}\)
3. Производная произведения: \((u* v)^{,}=u^{,}*v+ v^{,}*u\)
4. Производная частного двух функций: \((\frac{u}{v})^{,}=\frac{u^{,}v-uv^{,}}{v^{2}}\)

Предположим, что функция \(y = y(x)\) записана в параметрическом виде:

где t представляет собой параметр.

В таком случае первая производная рассматриваемой функции определяется по формуле:

\(y^{,}(x)=\frac{y^{,}_{t}}{x^{,}_{t}}\)

Если же функция \(y = y(x)\) задана неявно, справедливы уравнения \(F(x;y(x)) = 0\) или \(F(x;y(x)) = G(x;y(x))\), для определения первой производной \(y=y^{,}(x)\) следует использовать правила. На первом этапе дифференцируют каждую часть уравнения:

\((F(x;y(x)))^{,} = (0)^{,}\)

или

\((F(x;y(x)))^{,} = (G(x;y(x)))^{,}\)

Далее нужно определить производные от каждой из частей равенства, применяя таблицу производных и правила дифференцирования с учетом того, что y представляет собой сложную функцию. Полученное выражение можно использовать для определения \((y)^{,}\)

Решение задач с примерами

Требуется определить мгновенную скорость рассматриваемой точки.

Решение:

Производная пути по времени позволит рассчитать скорость точки

\(v(t)=s^{,}(t)=(4t^{2}+2t+1)^{,}=8t+2\)

Таким образом, в указанное время \(t_{0}=2\) точка движется со скоростью:

\(v(t_{0})=v(2)=8*2+2=18\)

Ответ: материальная точка перемещается со скоростью 18 м/с.

В какой-то момент показатели скорости будут равны v = 3 м/с. Необходимо рассчитать этот момент времени.

Решение:

Согласно физическому смыслу производной, скорость материальной точки будет изменяться по закону

\(v(t)=s^{,}(t)=(3t^{2}-3t-5)^{,}=6t-3\)

Определить момент времени \(t_{0}\) в который скорость точки достигла 3 м/с, можно с помощью записи и решения функции \(v(t_{0})=3.\)

\(6t_{0}-3=3\)

\(t_{0}=1\)

Ответ: скорость точки достигнет заданного значения в момент времени, равный 1с.

\(y=x^{2}-3x+\frac{x}{x+1}\)

Решение:

Производная, которую требуется найти, будет иметь вид

\(y^{,}=(x^{2}-3x+\frac{x}{x+1})^{,}\)

Исходя из того, что производная суммы или разности функций определяется как сумма или разность их производных, получим:

\(y^{,}=(x^{2})^{,}-(3x)^{,}+(\frac{x}{x+1})^{,}\)

Производная первой части уравнения рассчитывается по таблице производных, как производная степенной функции: \((x^{n})^{,}=nx^{n-1}\)

Таким образом:

\((x^{2})^{,}=2x^{2-1}=2x\)

Для преобразования второй части уравнения нужно использовать свойство производных и вынести константу 3 за знак производной:

\((3x)^{,}=3*(x) ^{,}\)

Затем определим производную по ранее записанной формуле из таблицы:

\((3x)^{,}=3*(x) ^{,}=3*(x^{1}) ^{,}=3*1*x^{1-1}=3*x^{0}=3*1=3\)

Производная третьей части уравнения является производной частного, и рассчитывается по формуле:

\((\frac{u}{v})^{,}=\frac{u^{,}v-uv^{,}}{v^{2}}\)

Если u=x, v=+1, то:

\((\frac{x}{x+1})^{,}=\frac{(x)^{,}*(x+1)-x*(x+1)^{,}}{(x+1)^{2}}=\frac{1*(x+1)-x*\left[(x)^{,} +(1)^{,}\right]}{(x+1)^{2}}=\frac{1}{(x-1)^{2}}\)

Таким образом:

\(y^{,}=2x-3+\frac{1}{(x-1)^{2}}\)

Ответ: \(y^{,}=2x-3+\frac{1}{(x-1)^{2}}\)

\(x (\operatorname{tg}x)’= \frac{1}{\cos^{2}x}\)

где

\(\quad x\neq\frac{\pi}{2}+k\pi\)

\(\quad k\in\mathbb{Z}\)

и

\((\operatorname{ctg}x)’=-\frac{1}{\sin^{2}x}\)

где

\(\quad x\neq k\pi\)

\(\quad k\in\mathbb{Z}\)

Решение:

Применяя правило дифференцирования частного, и учитывая, что

\((\sin x)’=\cos x\)

\((\cos x)’=-\sin x\)

получим выражение

\((\operatorname{tg}x)’=\left(\frac{\sin x}{\cos x}\right)’=\frac{(\sin x)’\cos x-(\cos x)’\sin x}{\cos^{2}x}=\frac{\cos^{2}x+\sin^{2}x}{\cos^{2}x}\)

Проведем аналогичные преобразования:

\((\operatorname{ctg}x)’=\frac{(\cos x)’\sin x-(\sin x)’\cos x}{\sin^{2}x}=-\frac{\sin^{2}x+\cos^{2}x}{\sin^{2}x}\)

Таким образом, выражения справедливы.