Вычисление производной функции
Как вычислить производную функцию
Производная функции — это концепция из математического анализа, которая позволяет найти скорость изменения функции по отношению к её независимой переменной. Она показывает, как функция меняется при малых изменениях аргумента.
Если у нас есть функция f(x), то производная функции f(x) обозначается f'(x) или dy/dx (где y представляет значение функции, а x — независимую переменную). Величина производной показывает, как быстро меняется значение функции при изменении аргумента x.
Геометрически производная в точке x определяет угол наклона касательной к графику функции в этой точке. Если производная положительна, график функции стремится вверх, если производная отрицательна, то график стремится вниз. Производная равна нулю в точках экстремума (локальных минимумах или максимумах).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
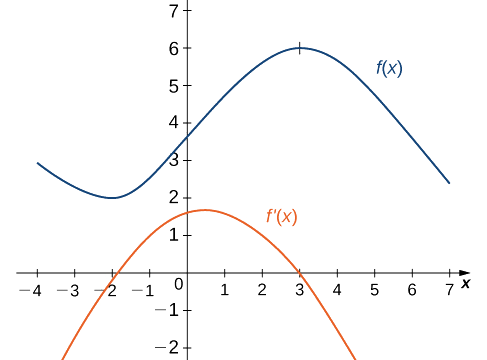
Используя следующий график f(x) для построения графика f′(x):
Источник: math.libretexts.org
Заметим, что f(x) возрастает и f′(x)>0 на (-2,3). Кроме того, f(x) убывает и f′(x)<0 на (-∞,-2) и на (3,+∞). Также заметим, что f(x) имеет горизонтальные касательные в точках -2 и 3, причем f′(-2)=0 и f′(3)=0.
Источник: math.libretexts.org
Производную функции можно вывести только по одной переменной, поэтому остальные переменные следует рассматривать как константы.
Простой способ вычисления производной функции — это вычисление предела. Если он существует, то вы имеете производную, иначе вы знаете, что функция не дифференцируема.
В качестве функции возьмем f(x) = x2.
(f(x+h)-f(x))/h = ((x+h)2 - x2)/h = (x2 + 2xh +h2 - x2)/h = 2x + h;
Теперь мы должны взять предел для h в 0, чтобы увидеть: f'(x) = 2x.
Формулы
Для вычисления производной функции существуют различные методы, в зависимости от сложности функции и доступности аналитического решения. Вот несколько основных методов:
-
Правило степеней: если функция вида \(f(x) = x^n\), то производная \(f'(x) = n * x^(n -1)\). Просто умножьте степень на исходное значение, и уменьшите степень на 1.
-
Правило суммы и разности: если f(x) = u(x) + v(x) или f(x) = u(x) - v(x), то производная f'(x) = u'(x) + v'(x) или f'(x) = u'(x) - v'(x). Просто возьмите производные от каждой функции и сложите (или вычтите) их.
-
Правило произведения: если f(x) = u(x) * v(x), то производная f'(x) = u'(x) * v(x) + u(x) * v'(x). Возьмите производную первой функции, умножьте на вторую функцию, и прибавьте к этому произведению второй функции, умноженной на производную первой функции.
-
Правило частного: если функция вида f(x) = u(x) / v(x), то производная \(f'(x) = [u'(x) * v(x) - u(x) * v'(x)] / [v(x)]^2\). Возьмите производные от числителя и знаменателя, и используйте формулу для частного.
-
Правило цепочки: если есть составная функция, например, f(x) = g(u(x)), то производная f'(x) = g'(u(x)) * u'(x). Возьмите производную внешней функции, затем производную внутренней функции, и перемножьте их.
Для тригонометрических и экспоненциальных функций существуют определенные правила, например:
- d/dx(sin(x)) = cos(x);
- d/dx(cos(x)) = -sin(x);
- \(d/dx(e^x) = e^x\);
- d/dx(ln(x)) = 1/x.
Примеры решения задач
Применение производных
Найти критические точки функции \(f(x) = 3x^3 - 9x^2 + 6x\).
Решение:
Чтобы найти критические точки, сначала нужно найти, где производная функции равна нулю или не существует.
Найдем производную функции f(x):
\(f'(x) = d/dx(3x^3 - 9x^2 + 6x)\)
\(f'(x) = 9x^2 - 18x + 6\)
Зададим f'(x) равной нулю и, решая для x, найдем критические точки:
\(9x^2 - 18x + 6 = 0\)
Используя квадратичную формулу или факторизацию, находим:
x = (18 ± √(18^2 - 4 * 9 * 6)) / (2 * 9)
x = (18 ± √(180)) / 18
x = (18 ± 6√5) / 18
x = 1 ± √5
Таким образом, критическими точками являются x = 1 + √5 и x = 1 - √5.
Прямоугольное поле необходимо огородить забором длиной 200 м. Найдите размеры прямоугольника, при которых площадь ограждения будет максимальной.
Решение:
Предположим, что длина прямоугольника равна x метров, а ширина — y метров.
Запишем уравнение для площади прямоугольника в терминах x и y: Площадь = x * y
Периметр = 2x + 2y = 200
Решим уравнение периметра для одной из переменных в терминах другой: y = 100 - x
Подставим значение y в уравнение площади: Площадь = \(x * (100 - x) = 100x - x^2\)
Найдем критические точки, взяв производную и приравняв ее к нулю:
d(Площадь)/dx = 100 - 2x
100 - 2x = 0
x = 50
Проверим конечные точки возможной области (0 ≤ x ≤ 100) и оценим площадь:
x = 0, площадь = 0
x = 100, площадь = 100 * (100 - 100) = 0
Максимальная площадь имеет место при x = 50, поэтому длина прямоугольника равна 50 м, а ширина y = 100 - 50 = 50 м.
Таким образом, для максимизации площади прямоугольное поле должно иметь размеры 50 м на 50 м.
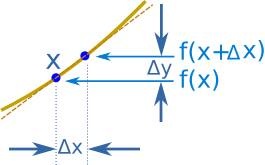
Для нахождения производной функции y = f(x) используется формула наклона:
Наклон = Изменение в Y/Изменение в X = Δy/Δx
Наклон дельты x и дельты y
Источник: mathsisfun.com
Из графика мы видим, что:
x изменяется от x до x+Δx;
y изменяется от f(x) до f(x+Δx).
Теперь выполним следующие действия:
Заполним формулу наклона:
Δy/Δx = (f(x+Δx) - f(x)) / Δx
Упростим его максимально:
Затем сделаем так, чтобы Δx уменьшалось до 0.
Например, так:
функция f(x) = x2
Мы знаем, что f(x) = x2, и можем вычислить f(x+Δx) :
Начнем с: f(x+Δx) = (x+Δx)2
Разложим (x + Δx)2: f(x+Δx) = x2 + 2x Δx + (Δx)2
Формула наклона имеет вид:
(f(x+Δx) - f(x))/Δx
Подставим f(x+Δx) и f(x):
(x2 + 2x Δx + (Δx)2 - x2)/Δx
Упростим (x2 и -x2 отменяются):
(2x Δx + (Δx)2) / Δx
Упростим еще больше (разделим на Δx):= 2x + Δx
Затем, когда Δx стремится к 0, получаем:= 2x
Результат: производная от x2 равна 2x.
Другими словами, наклон в точке x равен 2x.
Найти производную от f(x) = 3x2+ 2x-1
Решение:
Для нахождения производной заданной функции f(x), применим правило мощности и правило суммы дифференцирования.
Возьмем производную каждого члена отдельно.
- Для 3x2 производная будет 2*3x2-1 = 6x.
- Для 2x2 производная будет 2.
Объединим производные, используя правило суммы. Производная от f(x)=3x2+2x-1 равна f'(x)=6x+2.
Найти производную от g(x)= √x+(1/x)
Решение:
Для нахождения производной заданной функции g(x), воспользуемся правилом мощности и правилом дифференцирования взаимно обратных функций.
Возьмем производную каждого члена отдельно.
- Для √x можно записать в виде x1/2. Производная имеет вид 1/2x-1/2.
- Для 1/x, производная будет -1/x2.
Объединим производные, используя правило суммы.
Производная от g(x)= √x+(1/x) равна g'(x) = 1/2x-1/2 - 1/x2.
Найти производную функции \(f(x) = 3x^2 + 2x - 5\).
Решение: Для нахождения производной функции f(x) применим правило производных. Если мы имеем функцию вида \(f(x) = x^n\), то ее производная дается в виде \(f'(x) = nx^(n-1)\).
\(f(x) = 3x^2 + 2x - 5\)
\(f'(x) = d/dx (3x^2) + d/dx (2x) - d/dx (5)\)
\(f'(x) = 2 * 3x^(2-1) + 2 * 1x^(1-1) - 0\) (так как производная от константы равна нулю)
\(f'(x) = 6x + 2\)
Таким образом, производная функции \(f(x) = 3x^2 + 2x - 5\) равна f'(x) = 6x + 2.
Найти производную функции g(x) = sin(x) + cos(x).
Решение:
Для нахождения производной функции g(x) воспользуемся производными тригонометрических функций.
g(x) = sin(x) + cos(x)
g'(x) = d/dx (sin(x)) + d/dx (cos(x))
g'(x) = cos(x) - sin(x)
Таким образом, производная функции g(x) = sin(x) + cos(x) равна g'(x) = cos(x) - sin(x).
Найти производную функции \(h(x) = e^(2x).\)
Решение:
Для нахождения производной функции h(x) воспользуемся цепным правилом. Правило цепочки гласит, что если у нас есть функция вида f(g(x)), то ее производная дана в виде f'(g(x)) * g'(x).
\(h(x) = e^(2x)\)
\(h'(x) = d/dx (e^(2x))\)
\(h'(x) = e^(2x) * d/dx (2x)\)
\(h'(x) = e^(2x) * 2\)
Таким образом, производная функции \(h(x) = e^(2x) равна h'(x) = 2e^(2x).\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так