Сложение векторов в геометрии
Основные законы сложения векторов в геометрии
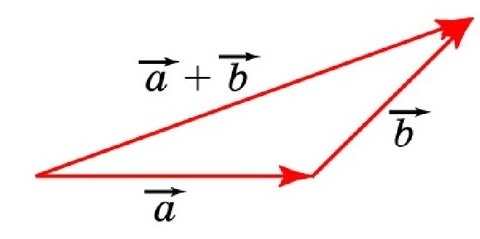
Суммой двух векторов \(\vec a+\vec b\) называют третий вектор \(\vec c\), который проведен из начала \(\vec a\) и упирается в конец \(\vec b\) при условии, что конец \(\vec a\) совпадает с началом \(\vec b\).
На плоскости найти сумму векторов можно, воспользовавшись формулой:
\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y\right\}\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если ситуация переходит в пространственное измерение, то достаточно всего лишь а тот же пример добавить новую координату:
\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y;a_z+b_z\right\}\)
Основные законы:
-
Переместительный закон (или коммутативный). Суть его свойства заключается в формуле: \(\vec a+\vec b=\vec b+\vec a\).
-
Сочетательный закон. Выглядит, как \(\left(\vec a+\vec b\right)+\vec c=\vec a+\left(\vec b+\vec c\right)\).
Помимо покоординатного сложения направленных отрезков, существуют геометрические нормы, которые позволяют узнать их сумму. Наиболее широко используемых методов в системе три: правило треугольника, параллелограмма и многоугольника.
Как происходит сложение по правилу треугольника
Чтобы узнать сумму векторов x и y, необходимо из произвольной точки отложить первый из них, а затем из его конца уже отложить второй. Следующий шаг — построить направленный отрезок, который соединит начало \vec x с концом \vec y. Образовавшаяся сторона треугольника и будет результатом сложения двух векторов. Теорема считается доказанной.
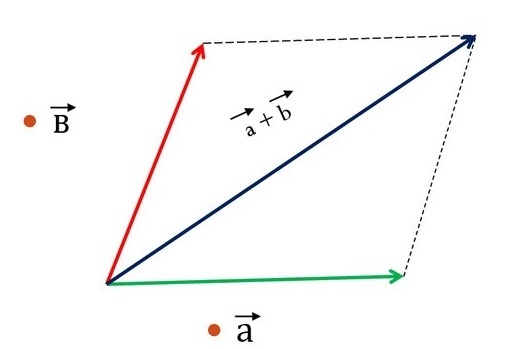
Сложение по правилу параллелограмма
Найти сумму векторов можно без построения треугольника. Для этого от начала первого вектора нужно отложить второй вектор. Дополним получившийся чертеж до параллелограмма. Две его стороны у нас уже имеются. Выстроить оставшиеся поможет способ параллельного переноса. Диагональ готовой фигуры, которая исходит из начальной точки векторов, считается их суммой. Теорема доказана.
Как и когда применяется правило многоугольника
Данный способ потребуется для того, чтобы сложить более двух векторов.
Принцип действий в данном случае похож на последовательность шагов, как в случае с треугольником. Из произвольной точки провести первый вектор. Из его конца — второй, из второго — третий и так далее. Затем окончание последнего вектора соединить с началом первого — это будет результат сложения всех векторов. Доказательство теоремы выполнено.
Задачи с примерами решения
Задача 1
Дано
\(\vec a=\left\{2; 3\right\}, \vec b=\left\{5; 7\right\}\).
Найти \(\vec a+\vec b\).
Решение
\(\vec a+\vec b=\left\{a_x+b_x;a_y+b_y\right\}=\left\{2+5; 3+7\right\}=\left\{7; 10\right\}\)
Задача 2
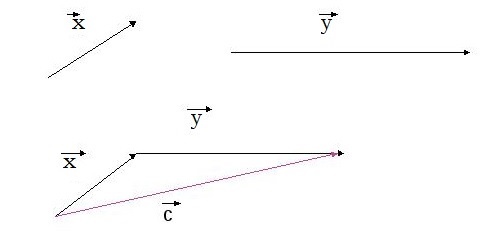
С помощью правила треугольника постройте сумму заданных векторов a и b.
Решение 1
Параллельным переносом совмещаем конец вектора a с началом b. Далее соединяем исходную точку вектора a с конечной вектора b. Выходит \(\vec c\). Длина отрезка, изображающего этот направленный отрезок, и будет общим значением \(\vec a\) и \(\vec b\).
Решение 2
С помощью параллельного переноса устанавливаем конец \(\vec b\) таким образом, чтобы он совпадал с началом \(\vec a\). Затем конечную точку первого совмещаем с началом второго. Получилось \(\vec c=\vec b+\vec a\).
Одна цель достигнута разными способами, что наглядно демонстрирует действие переместительного закона.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так