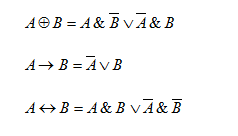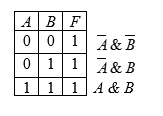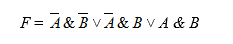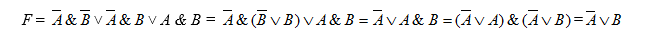Законы преобразования логических выражений
Что такое логические выражения
Логическим называют такое выражение, которое принимает формат символической записи с логическими параметрами в виде постоянных или переменных, связанных логическими действиями.
С целью определения справедливости какого-либо логического соотношения в распространенных случаях прибегают к построению таблицы истинности. В том случае, когда количество переменных в рассматриваемом выражении достаточно велико, озвученный метод не подходит для решения, так как сложно анализировать громоздкие табличные формы.
Целесообразно выбрать альтернативный метод в виде преобразования логических записей в равносильные с применением свойств операций из области логики, называемых закономерностями алгебры логики. В процессе подобных действий необходимо трансформировать выражения в более простые записи с учетом корректного порядка выполнения процедур, определения взаимосвязей между компонентами логических соотношений, выявления правильного варианта решения.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Преобразование логического выражения, которое не содержит в своем составе процедур импликации и эквиваленции, представляет собой формулировку равносильного соотношения с меньшим количеством действий конъюнкции и дизъюнкции при отсутствии отрицаний неэлементарных формул, либо с минимальной концентрацией переменных.
Введем ключевые обозначения, используемые для инициализации озвученных логических операций:
- X — логическое высказывание;
- \(\overline{Х}\) — инверсия;
- & — конъюнкция;
- \(\vee\) — дизъюнкция;
- \(\rightarrow\) — импликация;
- \(\leftrightarrow\) — эквиваленция.
Формулы
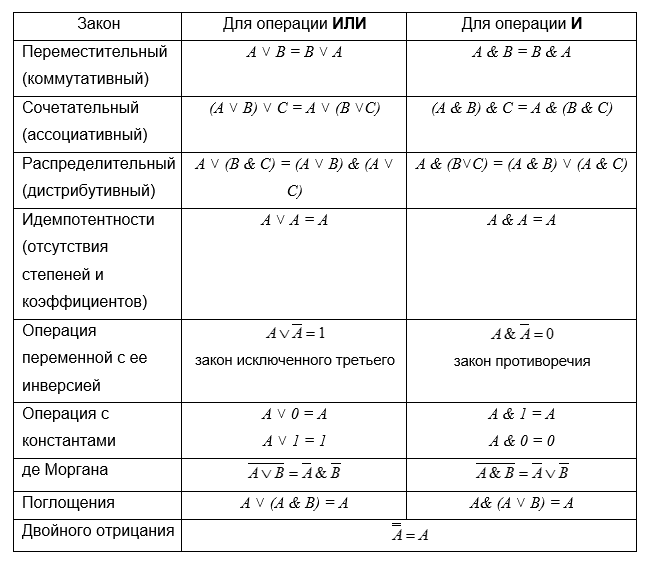
Существует ряд алгебраических законов логики, которые применяют в процессе решения заданий на логические выражения. Данные закономерности удобно представить с помощью формул. Рассмотрим озвученные соотношения, применимые к операциям «ИЛИ» и «И»:
Источник: resh.edu.ru
Правила преобразования логических выражений
Знание логических закономерностей способствует корректной и точной оценке разнообразных суждений и доводов. Ориентируясь на данные законы, несложно работать с громоздкими выражениями из области алгебры логики. Решение заключается в применении правил для упрощения сложных конструкций посредством замены их на упрощенные форматы записей без искажения смысла. Озвученный прием называют минимизацией функции.
Определенные трансформации логических выражений в информатике обладают сходствами с методами преобразования формул из классической алгебры. К примеру, к таковым относят вынесение единого множителя за знаки скобок, применение переместительного и сочетательного правила. Прочие принципы работы с логическими примерами подразумевают использование свойств, не характерных для тривиальных алгебраических задач. Например, в их числе распределительный закон конъюнкции, схемы для проведения поглощения, склеивания, формула де Моргана.
Пренебрежение логическими закономерностями сопровождается ошибками и дальнейшими противоречивыми утверждениями. Правильность законов подтверждают путем рассуждений, анализа выявленных сведений, построением табличных форм истинности. Разберем на примере использование правил преобразования выражений из области логики. Попробуем записать в более простом формате логические соотношения:
Источник: resh.edu.ru
Заметим, что в результирующей записи использованы только действия отрицания, конъюнкции и дизъюнкции. Подобный принцип формулировки логического выражения является нормальной формой. В процессе работы с задачами из алгебры логики нередко возникает необходимость в определении аналитического выражения для логического соотношения в соответствии с данными из таблицы истинности. В такой ситуации пригодятся понятия:
- совершенная дизъюнктивная нормальная форма;
- совершенная конъюнктивная нормальная форма.
В первом варианте речь идет о дизъюнктивной нормальной форме, состоящей из конъюнкции со всеми переменными. Второй случай распространяется на конъюнктивные нормальные формы с простыми дизъюнкциями, включающими в себя все переменные. При любом формате составления таблицы истинности допустимо сформулировать соответствующее ей логическое соотношение. Алгоритм действия при этом следующий:
- определить в исследуемой табличной форме совокупности переменных, обращающих параметр логического выражения в 1;
- формулировка конъюнкции для выявленных наборов в формате, предусматривающем включение переменной в конъюнкцию, если она равна 1, и ее отрицания при значении, отличном от 1;
- объединение полученных конъюнкций действиями дизъюнкции.
Примеры решения задач
Задана числовая прямая, содержащая отрезки B = [2;12] и C = [7;18]. Требуется определить величину отрезка А при условии, что следующий предикат соответствует истине при каком-либо значении х: \((х\in А)\vee ((х\in В)\rightarrow (х\in С))\) .
Решение
Проанализируем логическое выражение, записанное по условию задания. Заметим, что в данном случае допустимо исключить импликацию. Выполним соответствующие преобразования:
\((х\in А)\vee ((х\in В)\rightarrow (х\in С)) = (х\in А)\vee \overline{(х\in В)}\vee (х\in С)\)
В сформулированном выше равенстве А, В, С обозначают множества. Применительно к этим множествам допустимо представить следующую запись:
\(А \smile \overline{В} \smile С = U\)
За U принято универсальное множество. Предположим, что верным является такое соотношение:
\(\overline{А} = \overline{В} \smile С\)
По итогам преобразований допустимо сделать вывод о справедливости равенства:
\(А =\overline{\overline{В}\smile С} = В \frown \overline{С}\)
Найдено минимально допустимое множество А. Вернемся к условию задачи. Множество В соответствует отрезку на прямой линии [2;12]. Множество \( \overline{С}\) определено промежутками \(]-\infty;7[ и ]18;+\infty[\). При исходных данных получим в результате пересечения рассматриваемых множеств промежуток [2;7[.
Ответ: [2;7[ или другой промежуток, включающий в себя записанный.
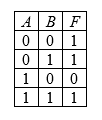
В соответствии с представленной ниже табличной формой истинности упростить заданное логическое выражение:
Источник: resh.edu.ru
Решение
Воспользуемся изученным ранее алгоритмом действий при работе с таблицами истинности. Выполним соответствующие преобразования и получим промежуточный результат:
Источник: resh.edu.ru
На следующей стадии допустимо составить подходящее логическое соотношение:
Источник: resh.edu.ru
Воспользуемся приемами для упрощения записи сформулированного выражения из алгебры логики. В процессе преобразований вынесем \(\overline{А}\) за знаки скобок. Далее целесообразно воспользоваться закономерностью исключенного третьего и распределительным способом. В итоге вычислений получим следующее равенство. Произведем необходимые алгебраические операции в уравнении и запишем результирующий ответ:
Источник: resh.edu.ru
Ответ:\( \overline{А} \vee В\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так