Геометрическая фигура призма: виды, свойства, элементы
Что такое призма
В жизни человека окружает множество геометрических фигур. Навыки определения их параметров являются полезными. В случае каждого объекта предусмотрены определенные правила и закономерности, которые значительно упрощают решение прикладных и теоретических задач. Одной из сложных и интересных фигур с точки зрения науки геометрии считают призму. Задания на вычисление сторон, площади, объема и прочих характеристик подобного объекта часто попадаются в контрольных и самостоятельных работах. Начнем с основного понятия этого геометрического объекта.
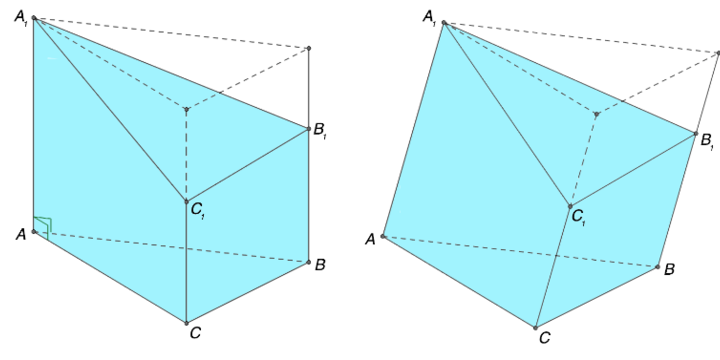
Призмой называют в геометрии пространственную фигуру в виде многогранника с парой параллельных и равных между собой граней, которые являются многоугольниками, и прочими гранями, имеющими форму параллелограммов.
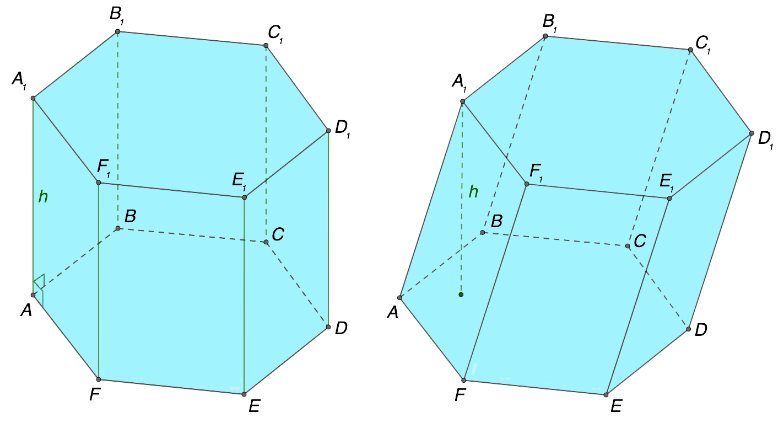
Разобраться со сформулированным определением достаточно сложно. По этой причине целесообразно трансформировать определение в графический рисунок. На изображении, представленном ниже, расположена четырехугольная призма. По-другому этот объект принято именовать параллелепипедом.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: microexcel.ru
Виды
Ранее была рассмотрена одна из самых простых разновидностей призмы. Существуют и другие конфигурации данного геометрического объекта. Ознакомимся с распространенными типами фигур, в основании которых треугольник. Начнем с прямой призмы. Таковой является объект с боковыми гранями, которые перпендикулярны относительно основания. Высота в прямой призме соответствует по величине ребру, расположенному сбоку. Ниже представлена типичная прямая призма.
Источник: microexcel.ru
Выделяют в отдельную категорию следующую разновидность призмы, называемой наклонной. В отличие от предыдущего типа геометрического объекта здесь предусмотрено другое расположение боковых граней относительно оснований. Рассматриваемые отрезки не перпендикулярны относительно друг друга, а находятся под каким-либо углом.
Источник: microexcel.ru
Как можно догадаться из названия, в основаниях правильной призмы расположены правильные многоугольники. В то же время этот геометрический объект способен обладать признаками прямой или наклонной фигуры. Представим на рисунке ниже описанную форму для наглядности:
Источник: microexcel.ru
Существует вид призмы, который получен путем некоторых действий. Так, например, при пересечении геометрического объекта какой-либо плоскостью, остается отдельный фрагмент, которому также свойственно определенная форма. Если используемая в процессе плоскость расположена не параллельно по отношению к основаниям призмы, то в результате получается ее часть, которую называют усеченной призмой. Как и в предыдущем примере, полученный путем несложных построений объект может быть отнесен к формату прямой или наклонной призмы. На рисунке для лучшего восприятия изображены оба варианта.
Источник: microexcel.ru
Свойства
Геометрическая фигура, которая обладает всеми признаками призмы, имеет ряд полезных свойств. Такие положения определены закономерностями, связывающими элементы объекта. Путем изучения оснований, сторон, граней и других составных компонентов призмы были получены комбинации, позволяющие значительно упростить расчеты характеристик рассматриваемой геометрической фигуры. Перечислим основные свойства и сопроводим их наглядными изображениями для того, чтобы упростить понимание механизма реализации и применения на практике.
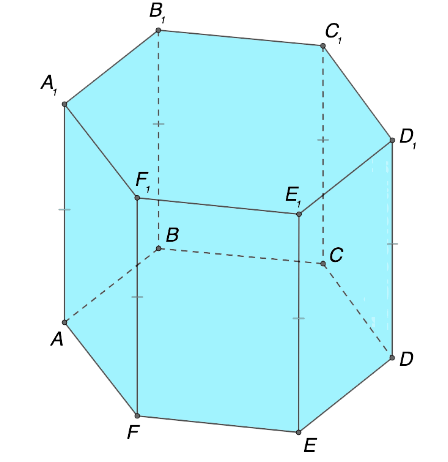
Проанализировать характерные для призмы свойства удобно на примере шестиугольного прямого объекта. Стоит отметить, что описанные ниже закономерности не являются индивидуальными, а имеют универсальный характер применения, то есть подходят для исследования и вычисления параметров любой призмы, независимо от ее разновидности. Начнем с равенства оснований призмы, которые являются многоугольниками.
Источник: microexcel.ru
Если ориентироваться на обозначения, сопровождающие рисунок выше, то получим справедливое равенство:
\(ABCDEF = A _{1}B_{1}C_{1}D_{1}E_{1}F_{1}\)
Следующее свойство, характерное ля призмы, заключается в форме граней, расположенных по бокам геометрического объекта. Данные грани являются параллелограммами. Обратимся вновь к ранее представленному изображению и перечислим соответствующие параллелограммы: \(AA_{1}B_{1}B, BB_{1}C_{1}C, CC_{1}D_{1}D, DD_{1}E_{1}E, EE_{1}F_{1}F и AA_{1}F_{1}F.\)
Другое полезное свойство призмы заключается в равенстве и взаимной параллельности всех боковых ребер геометрического объекта. Подобную закономерность стоит запомнить, так как это положение часто применяют в процессе решения разнообразных задач в курсе геометрии. Обозначим на графическом рисунке элементы призмы, о которых идет речь, и запишем корректное уравнение для описания примера.
Источник: microexcel.ru
\(AA_{1} = BB_{1} = CC_{1} = DD_{1} = EE_{1} = FF_{1}\)
\(AA_{1} \parallel BB_{1} \parallel CC_{1} \parallel DD_{1} \parallel EE_{1} \parallel FF_{1}\)
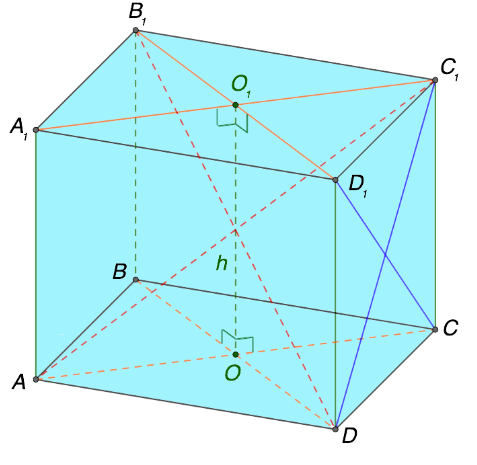
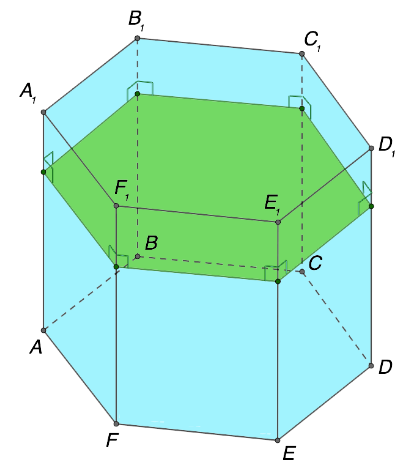
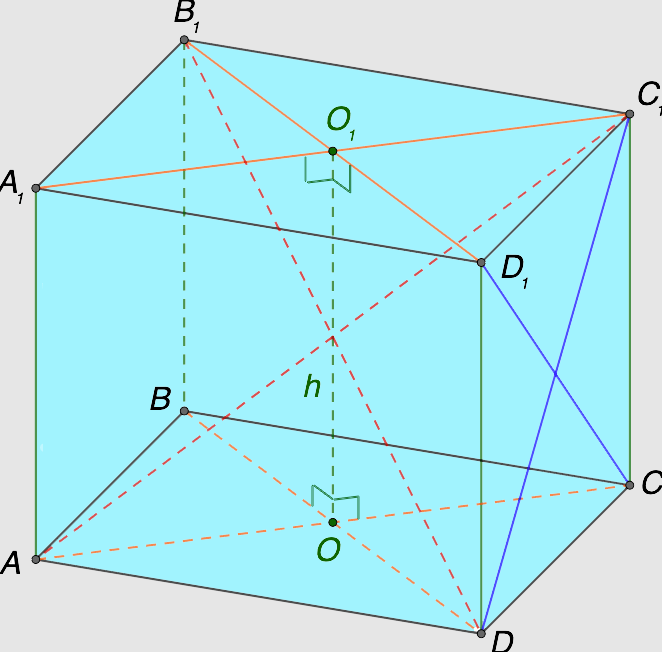
Еще одно важное свойство призмы заключается в расположении перпендикулярного сечения. Такая плоскость перпендикулярна относительно всех боковых граней и ребер геометрического объекта. Ознакомиться с прикладным применением данной характеристики можно на изображении ниже:
Источник: microexcel.ru
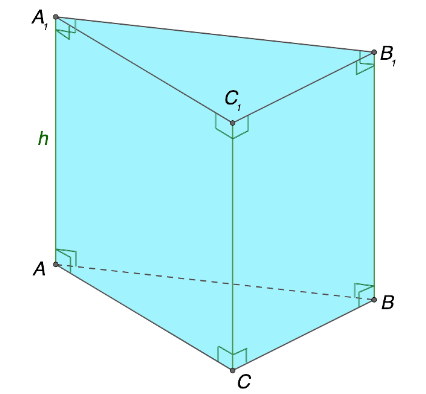
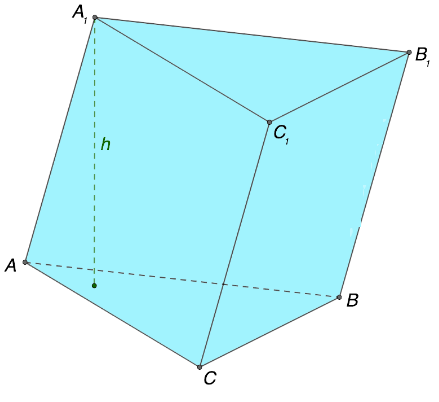
Следующая полезная закономерность состоит в соотношении между высотой и величиной бокового ребра. В какой-либо призме, являющейся наклонной, высота в любом случае будет меньше по сравнению с размером ребра, расположенного сбоку геометрической фигуры. Другая ситуация характерна для прямой призмы. В таком объекте высота по величине соответствует ребру.
Источник: microexcel.ru
Обращаясь к рисунку выше, допустимо сформулировать справедливые соотношения на примере элементов прямой и наклонной призмы соответственно:
\(h = AA_{1}\)
\(h < AA_{1} \)
Элементы
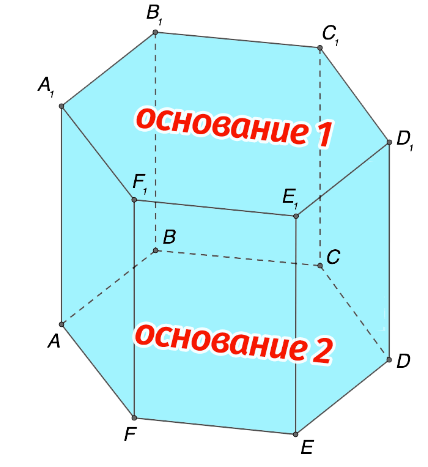
Перед тем, как приступить к разбору и решению геометрических задач, следует разобраться с терминологией. Введем понятия для всех основных компонентов призмы. Сделать это целесообразно, используя рисунок, представленный ниже:
Источник: microexcel.ru
Перечислим элементы геометрического объекта, сопровождая их соответствующими расшифровками:
- Основания имеют форму одинаковых многоугольников. В соответствии с форматом таких фигур определяют тип призмы. На рисунке выше представлен геометрический объект, обладающий основаниями в форме параллелограммов, а именно ABCD и \(A_{1}B_{1}C_{1}D_{1}1\).
- Боковые грани в данном примере изображены как параллелограммы и обозначены за \(AA_{1}B_{1}B, BB_{1}C_{1}C, CC_{1}D_{1}D и AA_{1}D_{1}1D\).
- Боковое ребро является отрезком, с помощью которого соединены соответствующие друг другу вершины разных оснований \((AA_{1}, BB_{1}, CC_{1} и DD_{1})\). Боковое ребро играет роль единой стороны прилегания пары боковых граней.
- Высота h представляет собой перпендикулярный отрезок прямой, обозначающий расстояние между парой оснований. Когда ребра по бокам призмы перпендикулярны рассматриваемым основаниям, считают, что такие ребра приобретают смысл высот геометрической фигуры.
- Диагональ основания изображена в виде отрезка, соединяющего пару вершин, расположенных друг напротив друга на едином основании. На изображении диагонали обозначены отрезками \(AC, BD, A_{1}C_{1} и B_{1}D_{1}\). Если речь в задаче идет о треугольной призме, то диагональ отсутствует.
- Диагональ боковой грани представляет собой отрезок, соединяющий пару вершин, которые расположены напротив друг друга и принадлежат одной грани. В геометрической фигуре, рассмотренной на графическом изображении, роль данных элементов играют отрезки \(CD_{1} и C_{1}D\).
- Диагональ призмы является отрезком, с помощью которого соединены две вершины, принадлежащие неодинаковым основаниям и разным боковым граням. В качестве примера таких компонентов геометрического объекта можно привести фрагменты прямых \(AC_{1} и B_{1}D\).
- Поверхность призмы является суммой поверхности пары оснований рассматриваемой фигуры и ее граней, расположенных по бокам.
Площадь поверхности призмы
После того, как сформировано понимание об основных элементах призмы и ее разновидностях, целесообразно перейти непосредственно к способам вычисления параметров геометрической фигуры. Стоит начать изучение с формул для выполнения расчетов и математических соотношений, которые предназначены для определения площади поверхности объекта. Запишем общую формулировку для вычисления площади полной поверхности геометрической фигуры:
\(S_{общ} = S_{бок} + 2S_{осн}\)
Если призма является прямой, то определить площадь боковой поверхности такой фигуры несложно, зная периметр основания и величину высоты:
\(S_{бок} = Р_{осн}\cdot h\)
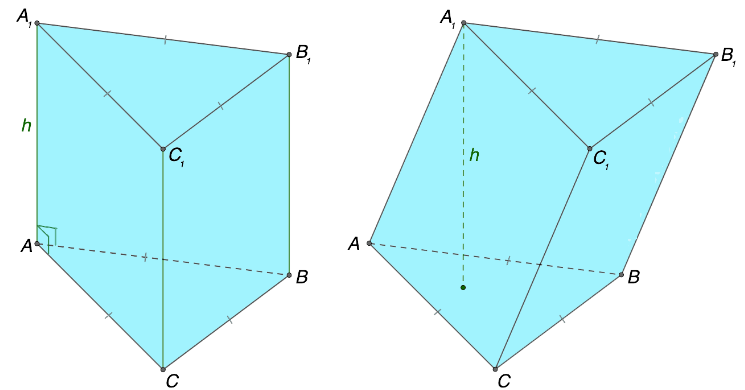
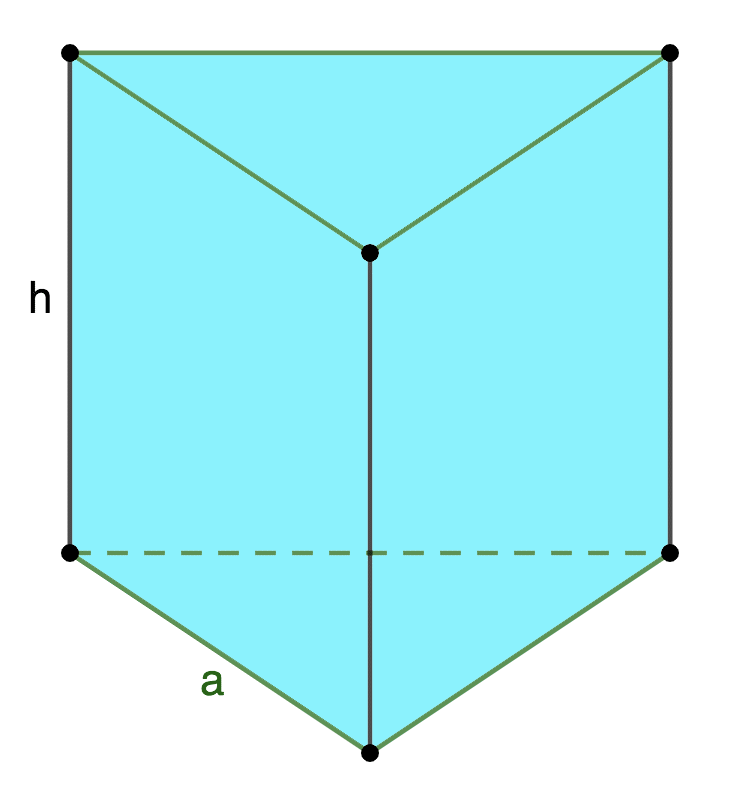
Далее запишем математические соотношения, выражающие закономерности между элементами правильной треугольной призмы, в основании которой лежит равносторонний треугольник:
Источник: microexcel.ru
\(S_{осн} = \frac{a^{2}\sqrt{3}}{4}\)
\(S_{бок} = 3аh\)
\(S_{полн} = 3аh + 2\frac{a^{2}\sqrt{3}}{4} = \frac{a^{2}\sqrt{3} + 6аh}{2}\)
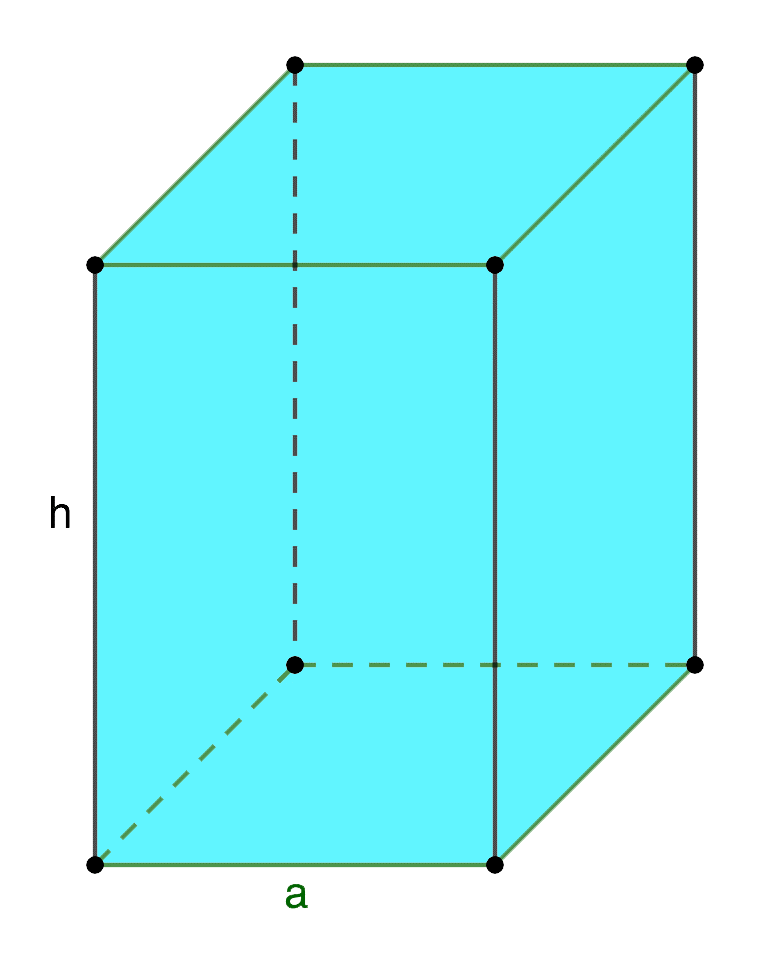
Если в задании по геометрии на расчет площади поверхности призмы речь идет о правильной четырехугольной фигуре с квадратом в основании, то целесообразно воспользоваться следующими формулами. Представим изображение такого геометрического объекта с соответствующими обозначениями и сопроводим рисунок несколькими полезными формулами.
Источник: microexcel.ru
\(S_{осн} = a^{2}\)
\(S_{бок} = 4аh\)
\(S_{полн} = 2a^{2}+ 4аh\)
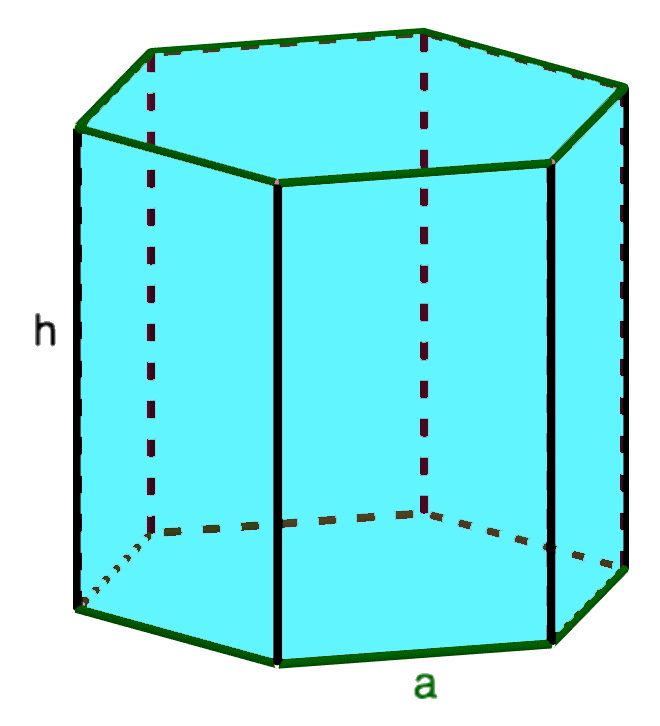
Рассмотрим следующий случай, который часто встречается в примерах по геометрии. Речь идет о правильной шестиугольной призме, основание которой представлено в виде правильного многоугольника с шестью углами.
Источник: microexcel.ru
\(S_{осн} = \frac{3\sqrt{3}a^{2}}{2}\)
\(S_{бок} = 6аh\)
\(S_{полн} = 6аh + 2\frac{3\sqrt{3}a^{2}}{2} = 6аh + 3\sqrt{3}a^{2}\)
Вычисление объема
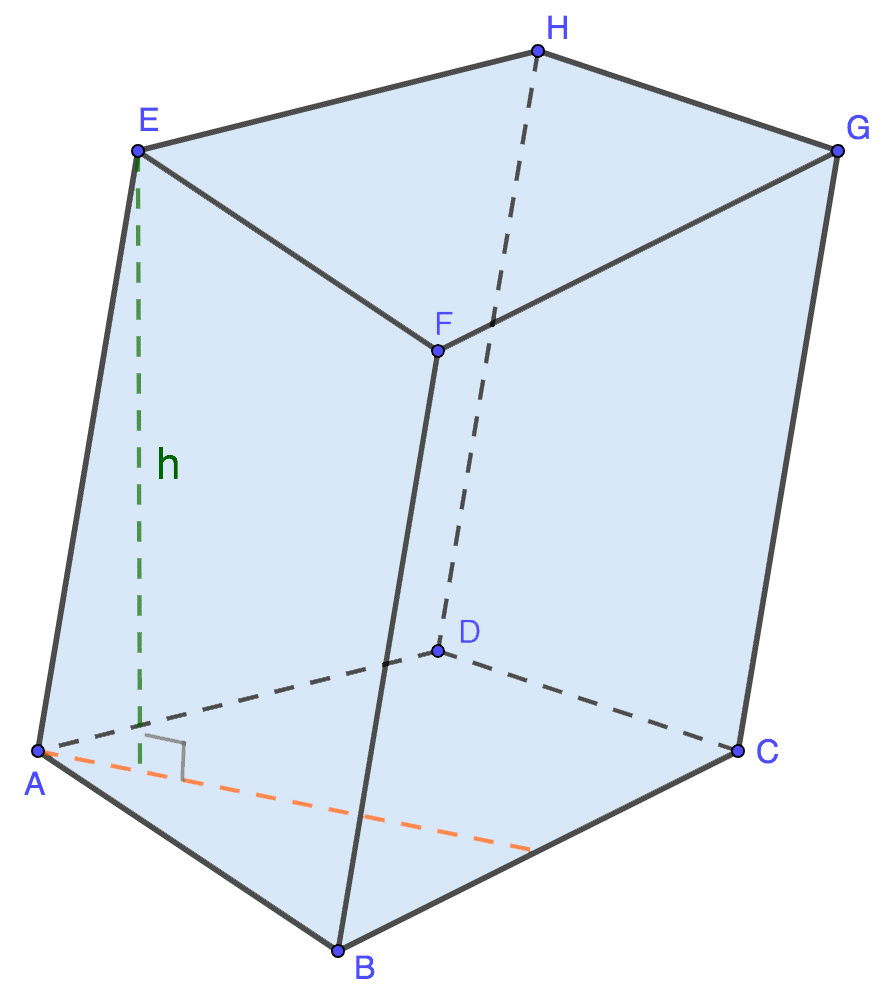
Рассмотрим произвольную призму из числа прямых, правильных или наклонных. Представим изображение на рисунке и обозначим все компоненты такого геометрического объекта.
Источник: microexcel.ru
Вычислить, чему равен объем такой призмы, можно с помощью следующей формулы:
\(V = S_{осн} \cdot h\)
Таким образом, для определения объема геометрического объекта, обладающего всеми признаками любой из перечисленных выше разновидностей призмы, следует найти результат от умножения площади основания и высоты фигуры. С целью расчета первого параметра необходимо рассмотреть многоугольник с четырьмя углами, который обозначен на рисунке за ABCD или EFGH.
Примеры решения задач
Сторона, входящая в состав геометрической фигуры в виде правильной треугольной призмы, соответствует 6 см. Высота рассматриваемого объекта равна 8 см. Требуется вычислить значение полной площади поверхности призмы.
Решение
Начнем решение задания с анализа условий. Заметим, что при известных элементах геометрического объекта, можно воспользоваться формулой, в которой они учтены. Остается только подставить численные значения величин, исходя из данной информации, и вычислить искомую площадь:
\(S_{полн} = \frac{6\cdot 6 \cdot 8 + 6^{2}\cdot \sqrt{3}}{2}\approx 175,18\)
Ответ: \(175,18 см^{2}\).
Правильная шестиугольная призма обладает площадью полной поверхности, которая равна \(400 см^{2}\). Сторона основания этой геометрической фигуры составляет 5 см. На основе имеющихся данных требуется рассчитать значение высоты рассматриваемого объекта.
Решение
С формулой для определения площади полной поверхности уже довелось поработать в процессе поиска ответа к предыдущей задаче. Из этой математической закономерности несложно выразить высоту. Запишем соответствующее соотношение и путем подстановки численных значений найдем искомую величину:
\(h = \frac{S_{полн} - 3\sqrt{3}a^{2}}{6a} = \frac{400 - 3\cdot \sqrt{3}\cdot 5^{2}}{6\cdot 5} \approx 9\)
Ответ: 9 см.
Имеется некая геометрическая фигура, обладающая формой призмы. Площадь основания данного объекта составляет \(14 см^{2}\). При этом высота соответствует величине в 6 см. Необходимо вычислить объем призмы.
Решение
Процесс поиска ответа к этой задаче не вызывает сложностей, если вспомнить основную формулу для вычисления объема призмы. Остается лишь подставить известные по условию задания значения, выполнить простые алгебраические преобразования и записать итоговый результат:
\(V = 14 \cdot6 = 84\)
Ответ: \(84 см^{3}.\)
Объем геометрического объекта, представленного в виде призмы, соответствует \(106 см^{3}\). Площадь основания рассматриваемой фигуры равна \(10 см^{2}\). Нужно рассчитать величину, которой соответствует высота этой призмы.
Решение
В данном случае общая формула для расчета объема призмы также будет полезна. Нужно только выразить с помощью озвученной закономерности высоту:
\(h = \frac{V}{S_{осн}} = \frac{106}{10} = 10,6\)
Ответ: 10,6 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так