Перпендикулярность двух плоскостей
Что такое перпендикулярность двух плоскостей
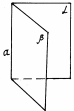
Двугранным углом называется фигура, образованная двумя различными полуплоскостями и прямой \(а\) — их общей границей.
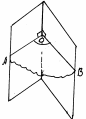
Линейным углом данного двугранного угла является \(\angle AOB\), где \(О\) — произвольная точка на прямой \(а\), а \(АО\) и \(ВО\) — перпендикуляры к прямой \(а\).
Градусной мерой двугранного угла называется градусная мера любого из его линейных углов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Две плоскости называют перпендикулярными, если угол между ними прямой \((90^\circ).\)
Примеры в повседневной жизни
- стена и потолок;
- грани коробки;
- спинка и сиденье стула.
Признак перпендикулярности плоскостей
Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости взаимно перпендикулярны.
Дано: \(\alpha,\beta\) — плоскости, \(\alpha\cap\beta\), \(а\) — прямая, \(а\in\beta, а\perp\alpha.\)
Доказать: \(\beta\perp\alpha\)
Доказательство:
Пусть \(a\cap\alpha=A, \alpha\cap\beta=b. а\perp\alpha\), значит а перпендикулярная любой прямой, принадлежащей плоскости \(\alpha\). В плоскости \(\alpha\) через точку \(А\) проведем прямую \(AC\), причем \(AC\perp b\). Из этого следует, что \(\angle BAC\) — линейный угол двугранного угла, образованного пересечением данных плоскостей. Мы знаем, что \(а\perp\alpha\), то есть и \(AB\perp\alpha\), значит \(\angle \)\(BAC=90^\circ\) и \((\widehat{\alpha;\beta})=90^\circ\). Плоскости \(\alpha\) и \(\beta\) перпендикулярны.
Если в плоскости есть хотя бы одна прямая, перпендикулярная другой плоскости, то эти плоскости взаимно перпендикулярны.
Если плоскость перпендикулярна прямой, по которой пересекаются две данные плоскости, то эта плоскость перпендикулярна каждой из данных плоскостей.
Свойства
- Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна другой плоскости.
- Если прямая, проведенная через точку одной из двух взаимно перпендикулярных плоскостей, перпендикулярна другой плоскости, то она лежит в первой из них.
- Теорема отвеса: если прямая, проведенная через точку одной из двух пересекающихся плоскостей, перпендикулярна другой плоскости и не лежит в первой, то данные плоскости не перпендикулярны.
- Если две плоскости, перпендикулярные третьей плоскости, пересекаются, то прямая их пересечения перпендикулярна третьей плоскости.
Примеры решения задач
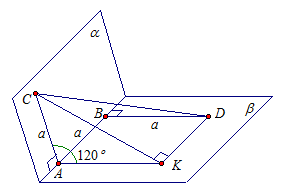
Точки А и В лежат на ребре данного двугранного угла, равного 120°. Отрезки \(АС\) и \(ВD\) проведены в разных гранях и перпендикулярны к ребру двугранного угла. Причем \(АВ=АС=ВD=а\). Найдите \(CD\).
Дано: двугранный угол \(CABD=120°, AC\perp AB, AC\subset\alpha, BD\perp AB, BD\subset\beta, AB=AC=BD=a.\)
Найти: \(CD\)
Решение:
Рассмотрим данный двугранный угол: в одной полуплоскости лежит точка \(C\) и прямая \(AC\), перпендикулярная прямой \(AB\), в другой полуплоскости лежит точка \(D\) и прямая \(BD\), перпендикулярная \(AB\). Проведем \(AK\) и \(DK,\) так что \(AK\perp AB, DK\parallel AB\). Тогда \(\angle KAC=120^\circ\) — линейный угол двугранного угла.
Рассмотрим четырехугольник \(AKBD\):
Мы знаем, что и \(AK\) и \(BD\) перпендикулярны \(AB\), значит они параллельны. \(AB\) так же параллельна \(DK\) по построению, значит \(AKBD\) — параллелограмм, а точнее прямоугольник. Из этого следует, что \(AK=BD=a.\)
Рассмотрим \(\triangle AKC:\)
По теореме косинусов: \(CK^2=AC^2+AK^2-2\cdot AC\cdot AK\cdot\cos\angle CAK=a^2+a^2-2\cdot a\cdot a\cdot\cos120^\circ=2a^2+a^2=3a^2\)
\(AB\perp(CAK)\), так как перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости, значит и \(DK\perp(CAK)\). Поэтому \(DK\perp CK\) и \(\triangle CKD\) —прямоугольный.
По теореме Пифагора:
\(CD=\sqrt{CK^2+KD^2}=\sqrt{3a^2+a^2}=2a\)
Ответ: \(2a\)
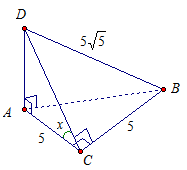
\(ABCD\) — тетраэдр (треугольная пирамида). \(\angle BAB=\angle DAC=\angle ACB=90^\circ, AC=CB=5, DB=5\sqrt5\). Найдите двугранный угол \(ABCD.\)
Дано: ABCD — тетраэдр, \(\angle BAB=\angle DAC=\angle ACB=90^\circ, AC=CB=5, DB=5\sqrt5.\)
Найти: \(\angle(ABCD)\)
Решение:
\(DA\perp(ABC)\) т.к. A\(B,\;AC\subset(ABC), AB\cap AC, DA\perp AB, DA\perp AC\). Тогда по теореме о трех перпендикулярах \(DC\perp BC\) (\(BC\) — прямая, \(AC\) — проекция DC на \((ABC), DC\) — наклонная). Значит \(\angle ACD\) — линейный угол искомого двугранного угла.
Рассмотрим прямоугольный \(\triangle CBD:\)
\(DC=\sqrt{DB^2-BC^2}=\sqrt{{(5\sqrt5)}^2-5^2}=10\)
Рассмотрим прямоугольный \(\triangle ACD:\)
\(\cos\angle ACD=\frac{AC}{DC}=\frac5{10}=\frac12\)
Получаем, что \(\angle ACD=arc\cos\frac12=60^\circ.\)
Ответ: \(60^\circ\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так