Признаки параллельных прямых

Что такое параллельные прямые

Для обозначения используется знак \(\parallel\). К примеру, \(a\parallel b\).

Отрезки и лучи, лежащие на параллельных прямых, тоже называются параллельными.

Для того чтобы определить параллельные прямые в трехмерном пространстве, важно учитывать, чтобы они лежали в одной плоскости.

Признаки параллельности прямых

Теорема 1

Докажем формулировку на примере задачи из геометрии.

Дано

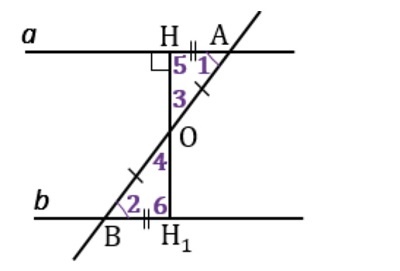
\(a\) и \(b\) — прямые, \(AB\) — секущая, \(\angle1=\angle2\), \(\angle1\) и \(\angle2\) — накрест лежащие.

Доказать: \(a\parallel b\).

Доказательство

Пример 1

Допустим, \(\angle1=\angle2=90^\circ\). Так как углы прямые — \(a\perp AB\) и \(b\perp AB\). Отсюда следует, что \(a\parallel b\).

Пример 2

Допустим, \(\angle1\) и \(\angle2\) не являются прямыми. Тогда из середины отрезка \(AB\) (обозначим ее точкой \(O\)) проведем перпендикуляр к прямой a и обозначим его, как \(OH\). Продолжим \(OH\) до прямой \(b\). Точку пересечения отметим, как \(H_1\).

Получившиеся треугольники \(OHA\) и \(OH_1B\) равны, так как:

• \(\angle3=\angle4\) — вертикальные;
• \(AO = OB\), так как \(O\) — середина отрезка;
• \(\angle1=\angle2\) — по условию.

Отсюда следует, что \(\angle5=\angle6\), и они прямые. Такой вывод можно сделать из того, что по построению \(OH\perp a\).

Так как \(HH_1\perp a\) и \(HH_1\perp b\), то \(a\parallel b\).

Теорема 2

Дано

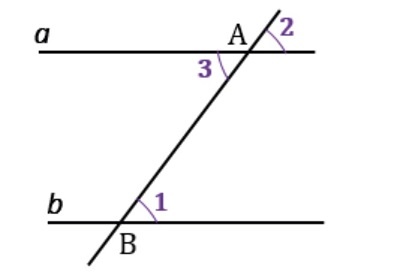
\(a\) и \(b\) — прямые, \(AB\) — секущая, \(\angle1=\angle2\), \(\angle1\) и \(\angle2\) — соответственные.

Доказать: \(a\parallel b\).

Доказательство

\(\angle2=\angle3\) — это следует из того, что углы вертикальные.

А так как по условию \(\angle1=\angle2\), получается, что \(\angle1=\angle3\). При этом они накрест лежащие. Следовательно, равенство доказывает, что \(a\parallel b\) (по теореме 1).

Теорема 3

Дано

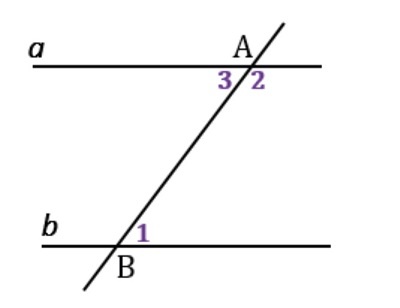
\(a\) и \(b\) — прямые, \(AB\) — секущая, \(\angle1+\angle2=180^\circ\), \(\angle1\) и \(\angle2\) — односторонние.

Доказать: \(a\parallel b\).

Доказательство

\(\angle3+\angle2=180^\circ\), так как они смежные.

Следовательно, \(\angle3=180^\circ-\angle2\).

\(\angle1+\angle2=180^\circ \)— по условию.

Следовательно, \(\angle1=180^\circ-\angle2\).

Отсюда вывод: \(\angle1=\angle3\).

А поскольку они накрест лежащие, это свойство дает право утверждать, что \(a\parallel b\) (по теореме 1).