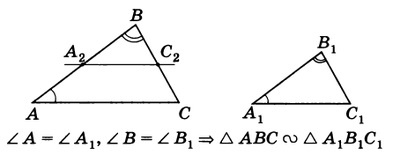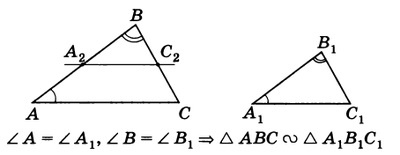Подобие треугольников: признаки и свойства

Подобие геометрических фигур

Обозначение подобия фигур: \(\sim\), например \(\triangle ABC\sim\triangle KLM\) (треугольник \(ABC\) подобен треугольнику \(KLM\))

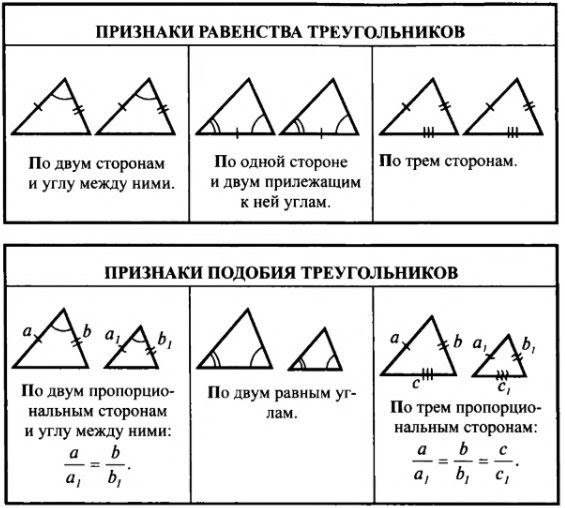
Признаки подобия треугольников

Для доказательства признаков подобия нам понадобится следующее утверждение:

Лемма

Первый признак: подобие по двум углам

Докажем данное утверждение.

Дано: \(\triangle ABC, \triangle A_1B_1C_1, \angle A=\angle A_1, \angle B=\angle B_1\)

Доказать: \(\triangle ABC\sim\triangle A_1B_1C_1\)

Доказательство:

Отложим на \(AB\) отрезок \(BA_2\), равный отрезку \(A_1B_1\) и проведем \(A_2C_2\parallel AC\). Рассмотрим \(\triangle A_1B_1C_1\) и \(\triangle A_2BC_2: A_1B_1 = A_2B\) по построению, \(\angle B=\angle B_1\) по условию и \(\angle A_1=\angle A_2\) как соответственные при параллельных прямых. Из леммы следует: \(\triangle A_2BC_2\sim\triangle ABC\), значит,\( \triangle ABC\sim\triangle A_1B_1C_1\).

Второй признак: по двум пропорциональным сторонам и углу между ними

Третий признак: по трем пропорциональным сторонам

Примеры задач

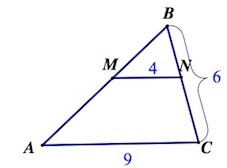
Задача 1

Через точки \(М\) и \(N\) на сторонах \(АВ\) и \(ВС\) треугольника \(ABC\) соответственно, проведена прямая \(МN\), параллельная стороне \(АС\), \(ВС = 6\), \(МN = 4\) и \(АС = 9\). Найдите длину \(СN\).

Решение:

Рассмотрим \(\triangle MBN\) и \(\triangle ABC\):

1. \(\angle B\) — общий
2. \(\angle BMN = \angle BAC\) как соответственные при \(MN\parallel AC\) и секущей \(AB\).

Следовательно \(\triangle MBN\sim\triangle ABC\)

Можем сделать вывод о пропорциональности соответствующих сторон: \(\frac{BN}{BC}=\frac{MN}{AC}=\frac{MB}{AB};\)

Пусть \(NC = x\), тогда \(BN = 6 - x\). Значит справедливо равенство: 

\(\frac{6-x}6=\frac49\)

\(9(6-x)=6\times4\)

\(x=\frac{10}3\)

Ответ: \(\frac{10}3\)

Задача 2

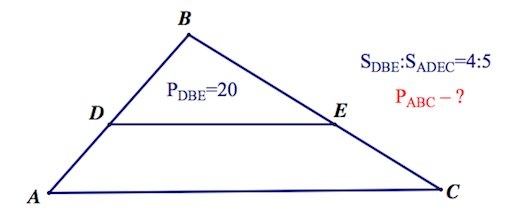
Прямая, параллельная основанию треугольника, отсекает от него треугольник и трапецию, площади которых относятся как 4:5 соответственно. Периметр маленького треугольника равен 20 см. Найти периметр данного треугольника.

Решение:

Имеем соотношение: \(\frac{S_{DBE}}{S_{ADEC}}=\frac45,\) значит \(\frac{S_{DBE}}{S_{ABC}}=\frac49\) (т.к. всего треугольник условно делится на \(4+5=9\) частей)

Рассмотрим \(\triangle DBE\) и \(\triangle ABC\):

1. \(\angle B\) — общий
2. \(\angle BDE = \angle BAC\) как соответственные при \(DE\parallel AC\) и секущей \(AB\)

Следовательно, \(\triangle DBE\sim\triangle AB\)C по двум углам.

Площади соотносятся как \(k^2\) (\(k\) — коэффициент подобия), значит \(k=\frac23\), то есть \(\frac{P_{DBE}}{P_{ABC}}=\frac23\), а так как \(P_{DBE}=20\), то выражаем \(P_{ABC}=30.\)

Ответ:30