Три признака равенства треугольников
Что значит равенство треугольников
Равенство треугольников — свойство двух фигур, в которых все элементы (три соответствующие стороны и соответствующие углы) равны.
Две фигуры являются равными тогда и только тогда, когда они могут быть полностью наложены друг на друга. Существуют различные условия для доказательства равенства. Фигура имеет шесть измерений — три стороны и три угла, и любое из трех указанных измерений может быть использовано для доказательства равенства.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Источник: natest.ru
Для обозначения конгруэнтности используется символ ≅.
Признаки равенства
Источник: onlinetestpad.com
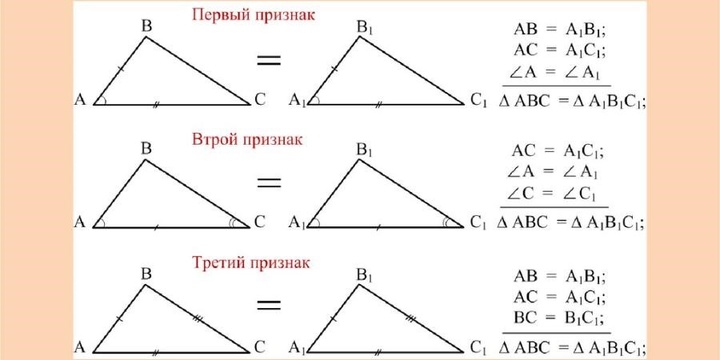
Первый
Постулат о конгруэнтности треугольников (УСУ) — фигуры конгруэнтны, если любые два угла и входящая в них сторона равны. Входящая сторона — это сторона между двумя углами.
На рисунке выше имеем △ABC и △A1B1C1. Заметим, что ∠A на △ABC равен ∠A1 на △A1B1C1, а ∠B на △ABC равен ∠B1 на △A1B1C1.
Есть включенная сторона между ∠A и ∠B на △ABC, которая равна длине стороны, входящей в треугольник ∠A1 и ∠B1 на △A1B1C1.
В этих двух треугольниках два угла конгруэнтны (равны), а входящая сторона между этими углами конгруэнтна. Таким образом, оставшийся угол △ABC должен быть равен:
180°−∠C−∠A
Это связано с тем, что внутренние углы складываются в 180 градусов. С заданными сторонами и углами можно построить только один треугольник (или его отражение).
Второй
Пожалуй, самый простой из трех постулатов — постулат о боковых сторонах (ССС) — треугольники являются равными, если три стороны одной фигуры равны соответствующим сторонам другой. Это единственный признак, в котором не рассматриваются углы.
Третий
Применяя постулат о боковом угле (УСУ). Здесь вместо выбора двух углов выбирают сторону и соответствующую ей сторону двух треугольников. Признак УСУ утверждает, что треугольники конгруэнтны, если любая пара соответствующих сторон и входящий в них угол конгруэнтны.
Для того чтобы две фигуры в △ABC и △A1B1C1 были конгруэнтны, три части — сторона, входящий угол и смежная сторона — должны быть конгруэнтны тем же трем частям — соответствующим стороне, углу и стороне — в другом треугольнике △YAK.
С помощью этих постулатов можно проверить равенство таких многоугольников, как параллелограмм, квадрат и прямоугольник.
Примеры решения задач
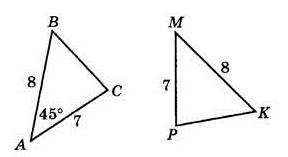
Проверьте, являются ли данные треугольники равными или нет, а также напишите критерий их равенства.
Решение: Определить конгруэнтность в данном случае.
Источник: geeksforgeeks.org
BC = QR = 4 единицы (дано);
CA = RP = 5 единиц (дано);
∠ABC = ∠PQR = 90°.
Теперь по условию конгруэнтности можно сделать вывод, что Δ ABC ≅ Δ PQR.
В Δ ABC, если AB = AC и ∠ B = 70°, найдите ∠ A.
Решение:
Дано: AB = AC и ∠B = 70°.
∠ B = ∠ C [Углы, противолежащие равным сторонам, равны].
Следовательно, ∠ B = ∠ C = 70°;
Сумма углов в треугольнике = 180°.
∠ A + ∠ B + ∠ C = 180°;
∠ A + 70° + 70° = 180°;
∠ A = 180° - 140°;
∠ A = 40°.
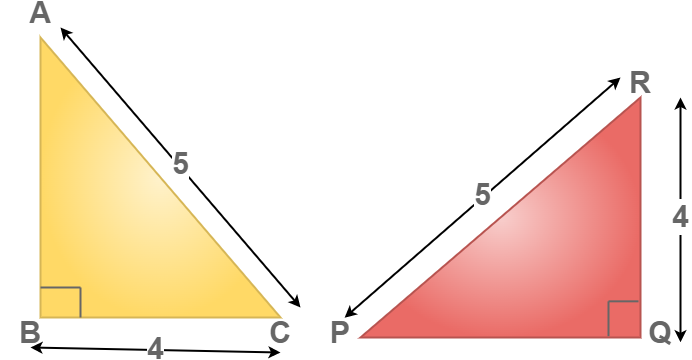
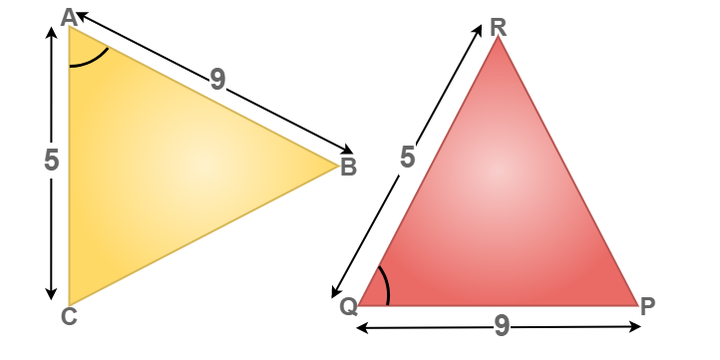
Проверьте, являются ли изображенные ниже фигуры равными или нет.
Источник: geeksforgeeks.org
Решение: AC = QR = 5 единиц (дано);
∠BAC = ∠PQR (дано);
BA = PQ = 9 единиц (дано).
Теперь по условию конгруэнтности УСУ можем заключить, что Δ BAC ≅ Δ PQR.
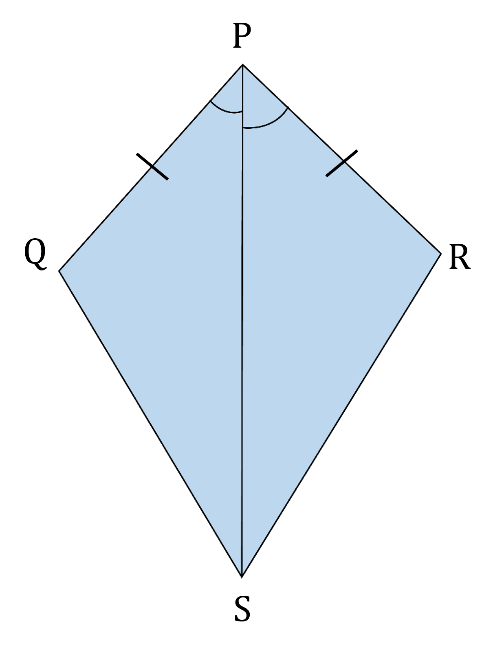
На данном рисунке PQ = PS и ∠QPR = ∠SPR. Докажите, что ∆ PQR ≅ ∆PSR, используя признак равенства СУС.
Источник: turito.com
Решение: В ∆ PQR и ∆ PSR,
PQ = PS (дано);
∠QPR = ∠SPR (дано);
PR = PR (общие стороны);
Следовательно, ∆PQR ≅ ∆PSR (по признаку СУС).
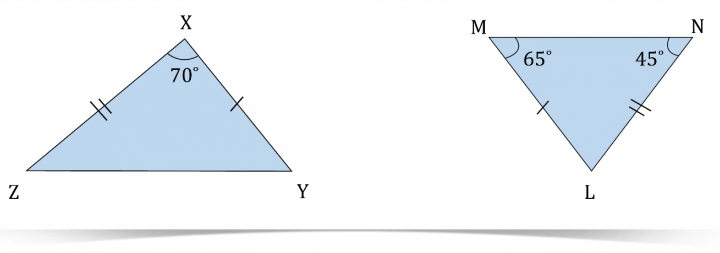
Определите равенство на данном рисунке.
Источник: turito.com
Решение: В ∆LMN,
65° + 45° + ∠L = 180°;
110° + ∠L = 180°;
∠L = 180° - 110°;
Следовательно, ∠L = 70°.
Теперь в ∆XYZ и ∆LMN.
∠X = ∠L (дано);
XY = LM (Дано);
XZ = NL (Дано);
Следовательно, ∆XYZ ≅ ∆LMN по постулату равенства СУС.
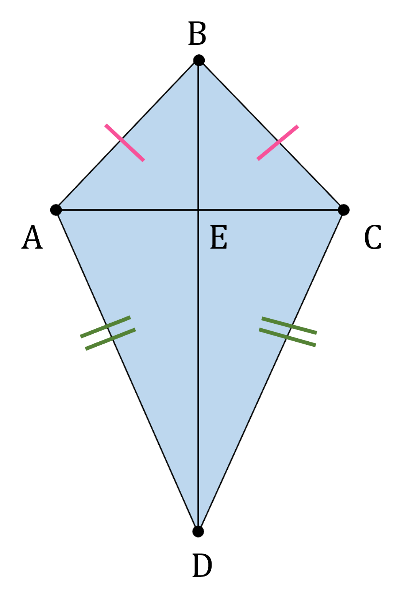
На данном рисунке AB = BC и AD = CD. Покажите, что BD пересекает AC под прямым углом.
Источник: turito.com
Решение: Из данного рисунка следует, что ∆ABD ≅ ∆CBD.
Дано: AB = BC и AD = CD.
Доказать, что ∠BEA = ∠BEC = 90° и AE = EC.
Доказательство:
AB = BC (дано);
AD = CD (дано);
BD = BD (общие стороны).
Следовательно, ∆ABD ≅ ∆CBD (по конгруэнтности ССС).
∠ABD = ∠CBD (Соответствующие углы).
Теперь из ∆ABE и ∆CBE;
AB = BC (Дано);
∠ABD = ∠CBD (Соответствующие углы);
BE = BE (Общие стороны);
Следовательно, ∆ABE≅ ∆CBE (по конгруэнтности SAS).
∠BEA = ∠BEC (Соответствующие углы).
И ∠BEA +∠BEC = 180° (линейная пара);
2∠BEA = 180° (∠BEA = ∠BEC);
∠BEA = = 90° = ∠BEC;
AE = EC (соответствующие стороны).
Следовательно, BD AC.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так