Производная и ее геометрический смысл

Что такое производная функция

С другой стороны, производную понимают в виде предела соотношения роста функции к увеличению ее аргумента, когда изменение аргумента приближается к нулевому значению, при условии существования такого предела.  В какой-то точке функция приобретает окончательную производную. Тогда можно говорить о том, что эта функция дифференцируема в определенной точке.

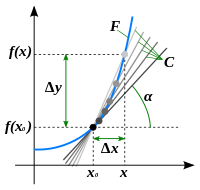
Термин производной достаточно просто изобразить наглядно с помощью такого графика:

 

Источник: ru.wikipedia.org

Разберем детально расшифровку термина производной. С этой целью представим, что в пространстве имеется точка \(x_{0}\in \mathbb{R}\)x, в которой обладает значением некая функция  \(f\colon U(x_{0})\subset \mathbb{R} \to \mathbb{R}\). На основе записанных сведений сформулируем понятие.

Далее рассмотрим понятие производной, используя определение предела. Предположим существование некоторой точки \(x_{0}\in \mathbb{R}\)x. Около этой точки принимает значения какая-то функция, к примеру,  \(f\colon U(x_{0})\subset \mathbb{R} \to \mathbb{R}\).

Во многих литературных источниках и учебниках можно встретить следующую формулировку производной:

\(f'(x_{0})=f'_{x}(x_{0})={\mathrm {D}}\!f(x_{0})={\frac {df}{dx}}(x_{0})=\left.{\frac {dy}{dx}}\right\vert _{{x=x_{0}}}={\dot {y}}(x_{0})\)

Как правило, выше записанное понятие характерно для теории в изучении механики и физики. Нередко подобная расшифровка термина встречается в исторических справочниках.

Геометрический смысл

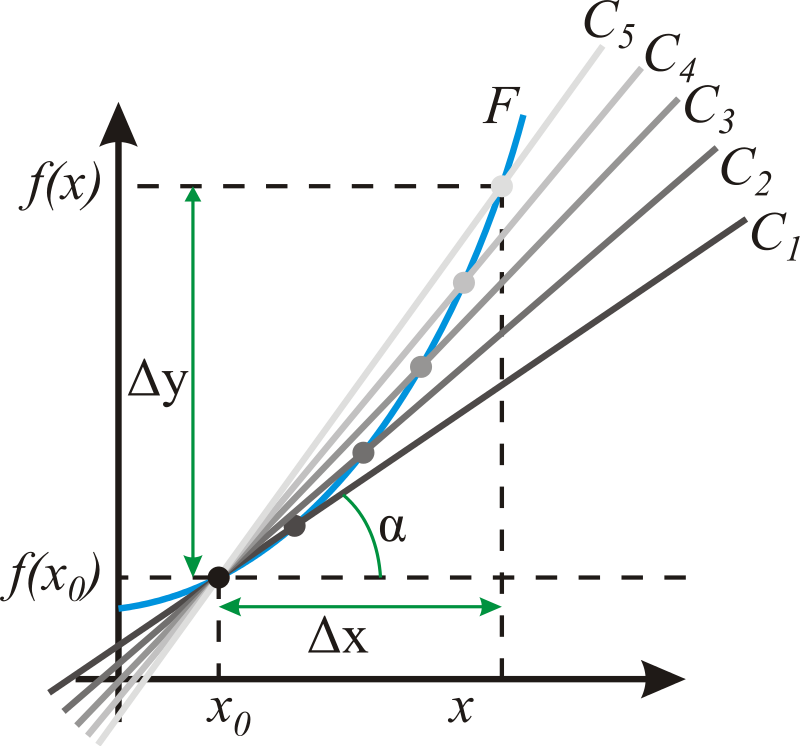
Производную можно объяснить с точки зрения геометрии. С этой целью потребуется изобразить график функции. Обозначим на нем абсциссу х0, а также определим ординату \(f(х0)\), которая ей соответствует. На окрестности абсциссы поставим какую-то точку х и начертим секущую линию, пересекающую точки графического изображения функции F. На схеме эта линия отмечена как С5. Удаленность друг от друга точек х и х0 стремится к нулевому значению и обозначается в виде дельта х. Таким образом, можно наблюдать переход секущей в касательную через линии С5, С4, С3, С2, С1. В результате производная, характерна для точки х0, представляет собой тангенс угла \(\alpha\).

 

Источник: ru.wikipedia.org

Правила вычисления производных с формулами

Перечислим справедливые закономерности, которые следует использовать в процессе вычисления производной функции, то есть при выполнении дифференцирования:

1. Постоянную переносят за знак производной таким образом: \({{\left( c\cdot f \right)}^{\prime }}=c\cdot {f}’\).
2. Производную от некоторой суммы можно вычислить с помощью формулы: \({{\left( f+y \right)}^{\prime }}={f}’+{y}’\).
3. Производную от умножения допустимо рассчитывать следующим способом:\({{\left( f\cdot y \right)}^{\prime }}={f}’\cdot y+f\cdot {y}’\) .
4. Производную от деления целесообразно вычислять с помощью соотношения: \({{\left( \frac{f}{y} \right)}^{\prime }}=\frac{{f}’y-f{y}’}{{{y}^{2}}}\).
5. Производная в случае вычислений сложной функции определяется таким образом: \({{\left[ f\left( y \right) \right]}^{\prime }}={f}’\left( y \right)\cdot {y}’\).

В процессе выполнения расчетов различных задач и примеров важно исключить ошибки в действиях. С этой целью полезно использовать простой алгоритм операций, позволяющий достаточно просто дифференцировать сложные функции:

1. Выявить функцию, которая записана внутри выражения, и определить, чему равна ее производная.
2. Записать функцию, расположенную снаружи, и аналогично выполнить ее дифференцирование.
3. Перемножить полученные значения после выполнения первого и второго этапа вычислений.

Примеры решения задач

Решение

Проанализируем запись из условия задачи. Заметим, что в данном случае целесообразно обратиться к свойству производной, которое состоит в ее линейности. Применительно к данному примеру, запишем следующее:

\(f'(x) = \left( x^{3}+2x^{2}-3x+5 \right)' = \left( x^{3} \right)'+\left( 2x^{2} \right)'-\left( 3x \right)'+\left( 5 \right)' = \left( x^{3} \right)'+ 2 \cdot \left( x^{2} \right)'- 3 \cdot \left( x \right)'+\left( 5 \right)'\)

Затем стоит обратиться к таблице, в которой записаны часто встречающиеся в решении задач производные, характерные для простейших функций. В итоге получим, что:

\(f'(x) = \left( x^{3} \right)'+ 2 \cdot \left( x^{2} \right)'- 3 \cdot \left( x \right)'+\left( 5 \right)' = 3x^{2} + 2 \cdot 2x - 3 \cdot 1 + 0 = 3x^{2} + 4x-3\)

Остается сформулировать и записать окончательный ответ.

Ответ: \(f'(x) = 3x^{2} + 4x-3\) 

Это означает, что решение легко упростить, воспользовавшись стандартным правилом дифференцирования суммы. При этом также необходимо исключить постоянную во втором по счету слагаемом. Приступим к поэтапным вычислениям:

\(f'(x) = \left( \text{arctg } x + 2 \ln x \right)' = \left( \text{arctg } x \right)' + \left( 2 \ln x \right)' = \left( \text{arctg } x \right)' + 2 \cdot \left( \ln x \right)'\)

Затем можно вновь обратиться к таблице производных. Подставим определенное значение в полученное ранее выражение и вычислим искомую величину:

\(f'(x) = \left( \text{arctg } x \right)' + 2 \cdot \left( \ln x \right)' = \frac{1}{1+x^{2}} + \frac{2}{x}\)

Ответ: \(f'(x)=\frac{1}{1+x^{2}} + \frac{2}{x}\).

Решение

Проанализируем условия задания. Заметим, что в условии примера речь идет о произведении. Вспомним, что имеется специальная формула, с помощью которой несложно определить значение производной от умножения. Воспользуемся этой закономерностью и выполним вычисления:

\(f'(x) = \left( (5x-3) \cdot 2^{x} \right)' = (5x-3)' \cdot 2^{x} + (5x-3) \cdot \left( 2^{x} \right)'\)

Здесь также подойдет таблица производных. Однако в данном случае нужно искать значения для степенной и показательной функций. После определения подходящего значения следует обратиться к правилу нахождения производной от разности. Выполним поэтапно запланированные действия и сформулируем окончательный ответ:

\(f'(x) = (5x-3)' \cdot 2^{x} + (5x-3) \cdot \left( 2^{x} \right)' = (5 \cdot 1 - 0) \cdot 2^{x} + (5x-3) \cdot 2^{x} \ln 2 = 5 \cdot 2^{x} + (5x-3) \cdot 2^{x} \ln 2\)

Ответ: \(f'(x) = 5 \cdot 2^{x} + (5x-3) \cdot 2^{x} \ln 2\)  

Решение

Заметим, что по условиям задачи можно говорить о поиске производной от деления. Воспользуемся соответствующей закономерностью дифференцирования и выполним необходимые вычисления:

\(f'(x) = \left( \frac{\ln x}{x^{2}} \right)' = \frac{(\ln x)' \cdot x^{2} - \ln x \cdot (x^{2})'}{\left( x^{2} \right)^{2}}\)

Далее целесообразно обратиться к таблице производных, которые определены в случае степенной и логарифмической функций. Это позволит избежать громоздких расчетов и исключить ошибки при определении значений. Выполним нужные действия и преобразуем конечный результат:

\(f'(x) = \frac{(\ln x)' \cdot x^{2} - \ln x \cdot (x^{2})'}{\left( x^{2} \right)^{2}} = \frac{\frac{1}{x} \cdot x^{2} - \ln x \cdot 2x}{x^{4}} = \frac{x -2x \ln x}{x^{4}} = \frac{x (1-2 \ln x)}{x^{4}} = \frac{1-2 \ln x}{x^{3}}\)

Ответ:\(f'(x) = \frac{1-2 \ln x}{x^{3}}\) .

Решение

Внимательно проанализируем выражение, записанное с правой стороны от знака функции в уравнении. Заметим, что данную по условию задания функцию достаточно просто преобразовать и записать как степень, имеющую показатель со знаком минуса. Таким образом, в выводе получим следующее соотношение:

\(f(x) = \left( \sqrt{x} \cdot e^{x} \right)^{-1}\)

В результате выполнен первый этап стандартного алгоритма работы с дифференцированием функций. Далее целесообразно воспользоваться уже знакомым из теоретического материала правилом поиска производной от сложной функции. В первую очередь вычислим, чему равна производная от начальной функции, как от степенной:

\(f'(x) = \left( \left( \sqrt{x} \cdot e^{x} \right)^{-1} \right)' = -\left( \sqrt{x} \cdot e^{x} \right)^{-2} \cdot \left( \sqrt{x} \cdot e^{x} \right)'\)

Затем допустимо вновь применить закономерность для дифференцирования. В этом случае выполним расчет производной от умножения пары функций. Таким образом, получим следующее выражение:

\(f'(x) = -\left( \sqrt{x} \cdot e^{x} \right)^{-2} \cdot \left( \sqrt{x} \cdot e^{x} \right)' = -\frac{1}{\left( \sqrt{x} \cdot e^{x} \right)^{2}} \cdot \left( \sqrt{x} \cdot e^{x} \right)' = - \frac{\left( \sqrt{x} \right)' \cdot e^{x} + \sqrt{x} \cdot \left( e^{x} \right)'}{x \cdot e^{2x}}\)

Воспользуемся уже привычной таблицей производных. С помощью подстановки готового значения в выражение выполним вычисления:

\(f'(x) = - \frac{\left( \sqrt{x} \right)' \cdot e^{x} + \sqrt{x} \cdot \left( e^{x} \right)'}{x \cdot e^{2x}} = -\frac{\frac{1}{2 \sqrt{x}} \cdot e^{x} + \sqrt{x} \cdot e^{x}}{x \cdot e^{2x}}\)

Полученное соотношение стоит преобразовать для удобной записи ответа:

\(f'(x) = -\frac{\frac{1}{2 \sqrt{x}} \cdot e^{x} + \sqrt{x} \cdot e^{x}}{x \cdot e^{2x}} = -\frac{e^{x}+ 2x \cdot e^{x}}{2x \sqrt{x} \cdot e^{2x}} =- \frac{e^{x}(2x+1)}{2x \sqrt{x} \cdot e^{2x}} = -\frac{2x+1}{2x \sqrt{x} \cdot e^{x}}\)

Ответ: \(f'(x) = -\frac{2x+1}{2x \sqrt{x} \cdot e^{x}}\).