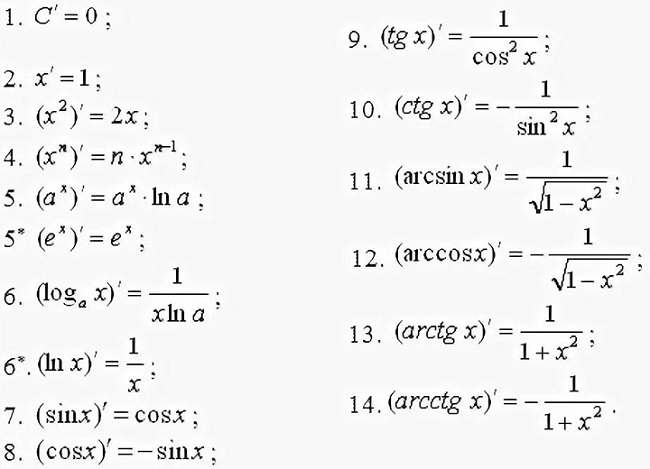Как решать производные с дробями

Производная дроби – что это такое

Формула производной от дроби

Формула ПД имеет следующий вид:

\(\left(\frac\upsilon\nu\right)'=\frac{\upsilon'\nu-\upsilon\nu'}{v^2}\)

При этом важно отметить, что нахождение ПД нельзя осуществлять с помощью деления производной числителя на производную знаменателя. Два эти действия будут иметь разные значения после подсчетов.

Приведем доказательство данной формулы. Рассмотрим выражение y=\frac\upsilon\nu. Все представленные переменные – это функции от х. Умножим их на \(\nu\). Получим \(y\times\nu=\upsilon\).

Дифференцируем по х, применяя формулу производной произведения двух функций, то есть:

\(\left(\upsilon\times\nu\right)'=\upsilon'\times\nu+\upsilon\times\nu'\)

Тогда выводим:

\(y'\times\nu+y\times\nu'=\upsilon'\)

Из этого вычисляем нужную нам производную:

\(y'\times\nu=\upsilon'-y\times\nu'=\upsilon'-\frac\upsilon\nu\times\nu'=\frac{\upsilon'v-\upsilon\nu'}\nu;\;y'=\frac{\upsilon'v-\upsilon\nu'}{\nu^2}\)

Что и требовалось доказать.

Следует также привести таблицу с производными часто встречающихся функций:

Как решать производные функции с дробями, примеры

Чтобы понять, как решать ПФ с дробями, приведем несколько примеров.

Пример 1

Найти производную дроби \(y=\frac x{In\;x}.\)

Решение

Из формулы следует, что числитель \(\upsilon=х\), а знаменатель \(\nu=In\;х\). Найдем их производные:

\(\upsilon'=\left(х\right)'=1,\;\nu'=\left(In\;x\right)'=\frac1x\)

Подставляем решенные \(\upsilon'\;и\;\nu'\) в формулу и получаем:

\( y'=\left(\frac x{In\;x}\right)'=\frac{\left(x\right)'In\;x-x\left(In\;x\right)'}{\left(In\;x\right)^2}=\frac{In\;x\;-x{\displaystyle\frac1x}}{In^2x}=\frac{In\;x-1}{In^2x}\)

Ответ: \(y'=\frac{In\;x-1}{In^2x}.\)

Пример 2

Найти производную дроби, равную \(y=\frac{\cos\;x}x\).

Решение

По формуле производной частного:

\(y'=\left(\frac{\cos\;x}x\right)=\frac{\left(\cos\;x\right)'x-\cos\;x\left(x\right)'}{\left(x\right)^2}\)

Производная косинуса дает нам синус с минусом:

\(\left(\cos\;x\right)'=-\sin\;x\)

В таком случае:

\(y'=\frac{-x\;\sin\;x-\cos\;x}{x^2}=-\frac{x\;\sin\;x+\cos\;x}{x^2}\)

Ответ: \(y'=-\frac{x\;\sin\;x+\cos\;x}{x^2}.\)

Пример 3

Найти производную дроби \(y\left(x\right)=\frac{e^x-1}{e^x+1}.\)

Решение

Из таблицы производных находим:

\(\left(e^x\right)'=e^x\)

Применяем правила дифференцирования постоянной и суммы:

\(\left(e^x-1\right)'=\left(e^x\right)'-\left(1\right)'=e^x-0=e^x;\;\left(e^x+1\right)'=\left(e^x\right)'+\left(1\right)'=e^x-0=e^x\)

Используем формулу производной дроби:

\(\left(\frac\upsilon\nu\right)'=\frac{\upsilon'\nu-\upsilon\nu'}{\nu^2};\left(\frac{e^x-1}{e^x+1}\right)'=\frac1{\left(e^x+1\right)^2}\times\lbrack\left(e^x-1\right)'\left(e^x+1\right)-\left(e^x-1\right)\left(e^x+1\right)'\rbrack=\frac1{\left(e^x+1\right)^2}\times\lbrack e^x\left(e^x+1\right)-\left(e^x-1\right)e^x\rbrack=\frac{2e^x}{\left(e^x+1\right)^2}\)

Ответ: \(y'=\frac{2e^x}{\left(e^x+1\right)^2}.\)