Производная экспоненциальной функции

Производная экспоненциальной функции

В данном случае n допустимо взять из множества натуральных или действительных чисел.

\((е^{х})' = е^{х}\)

Вывод производной от экспоненты в степени x

Запишем условия для проведения доказательств: \(e^x\) с условием, что \(x = (-\infty; +\infty)\). При этом:

\(y'=\lim\limits_{\Delta x\to 0} \frac{e^{x+\Delta x}-e^x}{\Delta x}\)

Обратимся к особому свойству, характерному для экспоненты:

\(e^{a+bx}=e^a \cdot e^b\)

Заметим, что в данном случае имеется возможность для преобразования числителя в пределе:

\(e^{x+\Delta x}-e^x = e^x*e^{\Delta x}-e^x = e^x(e^{\Delta x}-1)\)

Таким образом:

\(y'=\lim\limits_{\Delta x\to 0} \frac{e^{x+\Delta x}-e^x}{\Delta x}=\lim\limits_{\Delta x\to 0} \frac{e^x(e^{\Delta x}-1)}{\Delta x}\)

Целесообразно ввести следующее обозначение:

\(t=e^{\Delta x}-1\)

В результате запишем такое выражение:

\(е^{\Delta x}=t+1\)

В логарифмическом свойстве говорится о том, что:

\(\Delta x = ln(t+1)\)

Заметим, что в данном случае экспонента не прерывается. По этому условию сделаем следующий вывод:

\(\lim\limits_{\Delta x\to 0} e^{\Delta x}=e^0=1\)

В том случае, когда \(\Delta x\) стремится к нулевому значению, будет корректно записать, что t стремится к нулевому значению. Выполним необходимые вычисления:

\(y'=\lim\limits_{\Delta x\to 0} \frac{e^{\Delta x}-1}{\Delta x}=e^x\lim\limits_{t\to 0}\frac{t}{ln(t+1)}\)

Введем следующее обозначение:

\(n=\frac {1}{t}\)

В результате получим, что:

\(t=\frac{1}{n}\)

Если выполняется условие, при котором t стремится к нулевому значению, то n будет стремиться к бесконечности. Выполним соответствующие преобразования предела:

\(y'=e^x\lim\limits_{t\to 0}\frac{t}{ln(t+1)}=e^x\lim\limits_{n\to\infty}\frac{1}{n\cdot ln(\frac{1}{n}+1)^n}\)

Обратимся вновь к логарифмическому свойству:

\(b\cdot ln c=ln c^b\)

В результате получим, что:

\(n\cdot ln (\frac{1}{n}+1)=ln(\frac{1}{n}+1)^n=ln(1+\frac{1}{n})^n\)

Целесообразно переписать предел таким способом:

\(y'=e^x\lim\limits_{n\to\infty}\frac{1}{n\cdot ln(\frac{1}{n}+1)} = e^x\lim\limits_{n\to\infty}\frac{1}{ln(\frac{1}{n}+1)^n}= e^x\frac{1}{\lim\limits_{n\to\infty} ln(\frac{1}{n}+1)^n}\)

Заметим, что в данном случае можно применить свойство непрерывности логарифма и свойство, характерное для пределов, когда функция не прерывается. В итоге получим:

\(\lim\limits_{x\to x_0}ln(f(x))=ln(\lim\limits_f(x))\)

Заметим, что функция f(x) обладает пределом со знаком плюс.

\(\lim\limits_{x\to x_0}f(x)\)

Непрерывный логарифм и существование предела со знаком плюс, то есть:

\( \lim\limits_{n\to\infty}(\frac{1}{n}+1)^n\)

дают нам право заключить следующее:

\(\lim\limits_{n\to\infty}ln(1+\frac{1}{n})^n=ln\lim\limits_{n\to\infty}ln(1+\frac{1}{n})^n=ln e=1\)

В этой ситуации целесообразно оперировать значением, которое имеет второй замечательный предел:

\(\lim\limits_{n\to\infty}(1+\frac{1}{n})^n=e\)

В результате:

\(y'= e^x\frac{1}{\lim\limits_{n\to\infty} ln(\frac{1}{n}+1)^n} = e^x\cdot\frac{1}{ln e} = e^x\cdot\frac{1}{1}=e^x\)

Получилось доказать справедливость исходного равенства:

\((e^x)'=e^x\)

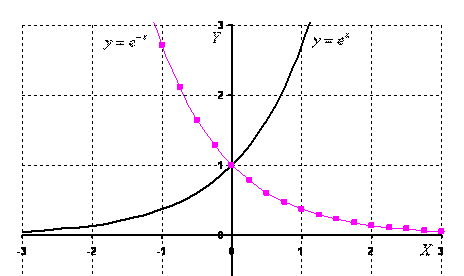
Графики экспоненциальных функций

Источник: mathprofi.ru

Примеры решения задач

Решение

Воспользуемся рассмотренным ранее правилом. Получим, что необходимая производная вычисляется таким образом:

\(y^{\prime}(x)=\left(e^{2 x}\right)^{\prime}\)

Заметим, что в данном случае экспонента обладает степенью, записанной в виде сложной функции. Тогда целесообразно выполнить умножение производной от экспоненты на производную от степени. В итоге получим:

\(y^{\prime}(x)=e^{2 x} \cdot(2 x)^{\prime}\)

Достаточно просто продолжить вычисления, если избавиться от постоянной в знаке производной. Перенесем ее таким способом:

\(y^{\prime}(x)=e^{2 x} \cdot 2 \cdot(x)^{\prime}=2 e^{2 x} \cdot 1=2 e^{2 x}\)

Ответ: \(y^{\prime}(x)=2 e^{2 x}\)y

Решение

Воспользуемся уже знакомым алгоритмом расчетов и произведем необходимые вычисления для поиска требуемой производной:

\(y^{\prime}(x)=\left(2 e^{x}\right)^{\prime}\)

Заметим, что в данном случае допустимо избавиться от постоянной путем ее переноса за знак производной. Выполним необходимые преобразования и запишем готовый ответ к заданию:

\(y^{\prime}(x)=2 \cdot\left(e^{x}\right)^{\prime}=2 \cdot e^{x}=2 e^{x}\)

Ответ: \(y^{\prime}(x)=2 e^{x}\).