Теорема о пропорциональных отрезках в прямоугольном треугольнике

Признак подобия прямоугольных треугольников

Признак подобия треугольников с прямым углом является частным случаем первого признака подобия треугольников, который предполагает следующее: при соответствии двух углов одного треугольника двум углам другого такие треугольники являются подобными.

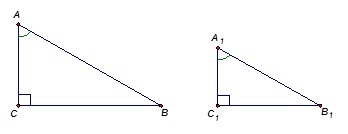
Рассмотрим наглядно на схеме:

∠C=∠C₁=90°

∠A=∠A₁

∠B=180°−(∠C+∠A)

∠B₁=180°−(∠C₁+∠A₁)

Отсюда следует, что ΔABC∼ΔA₁B₁C₁.

Пропорциональные отрезки в прямоугольном треугольнике — отношение

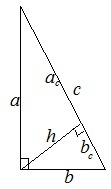
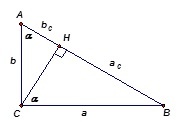
На рисунке изображен прямоугольный треугольник с катетами a и b, гипотенузой c и проведенной к ней высоте h. Высота делит гипотенузу на два отрезка: a_c и b_c, именуемые проекциями катетов на гипотенузу.

Доказательство

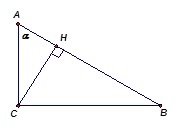
Пусть в ΔABC ∠C=90°, ∠A=α, CH – высота.

1. Сначала докажем, подобие ΔABC и ΔCBH.  

Поскольку CH – высота, то ∠CHB равен 90°.

∠B=90°−α – это общий угол рассматриваемых треугольников ABC и CBH.

∠HCB=90°−∠B=90°−(90°−α)=α.

Следовательно, в ΔABC и ΔCBH: 

∠ACB=∠HCB=90°

∠B – общий и равен 90°−α

∠CAB=∠HCB=α

Отсюда следует, что ΔABC∼ΔCBH.

2. Теперь докажем, что ΔABC∼ΔACH. 

∠ACB=∠AHC=90°, т.к. СН – высота ΔABC.

∠A – общий и равен α.

∠ACH=90−α, а значит, равен ∠AВC.

Следовательно, ΔABC∼ΔACH.

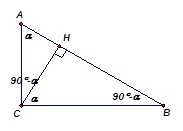
3. Сделаем на схеме дополнительные обозначения проекций катетов:

4. Применим доказанное подобие ΔABC и ΔCBH и запишем пропорции сторон: 

\(\frac ac=\frac{a_c}a\)

В переводе с математического языка это означает следующее: отношение противолежащих прямому углу сторон, ровняется отношению сторон, расположенных напротив угла α. Из данного соотношения получается:

\((1)a^2=a_c\times c\)

5. Воспользуемся тем, что ΔABC∼ΔACH. Запишем пропорции сторон: 

\(\frac bc=\frac{b_c}b\)

Это значит, что отношение сторон, противолежащих прямому углу равно отношению сторон, лежащих напротив α. Выведем из пропорции следующее уравнение:

\((2)b^2=b_c\times c\)

Полученные равенства (1) и (2) доказывают теорему.

Доказательство:

Поскольку ранее мы доказали подобия треугольников ΔABC∼ΔCBH и ΔABC∼ΔACH, то ΔCBH∼ΔACH. Используем этот факт для доказательства второй теоремы. Запишем пропорцию: 

\(\frac h{a_c}=\frac{b_c}h\)

Она значит, что отношение сторон, противолежащих углу (90°−α), равно соотношению сторон, противолежащих углу α. 

Выведем отсюда значение h:

\(h^2=a_c\times b_c\)

Теорема доказана.

Альтернативное доказательство теоремы Пифагора

Сформулированные и доказанные теоремы позволяют привести альтернативу традиционному доказательству пифагоровой теоремы:

\(\left.\begin{array}{r}b^2=b_c\times c\\a^2=a_c\times c\end{array}\right\}\Rightarrow a^2+b^2=a_c\times c+b_c\times c=c\left(a_c+b_c\right)=c\times c=c^2\)

Примеры решения задач на использование пропорциональных отрезков в прямоугольном треугольнике

Задача 1

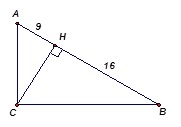
В ΔABC: ∠С=90°, СН – высота, отрезок АН=9 см, отрезок АН=16 см. Вычислите длину катетов и высоты треугольника ABC.

Решение

1. Определим длину гипотенузы: AB=9+16=25 см.
2. Применим доказанные теоремы:

\(BC=\sqrt{AB\times BH}=\sqrt{25\times16}=5\times4=20\)

\(AC=\sqrt{AB\times AH}=\sqrt{25\times9}=5\times3=15\)

\(CH=\sqrt{BH\times AH}=\sqrt{16\times9}=4\times3=12\)

Ответ: сторона ВС=20 см, сторона АС=15 см, высота СН=12 см.

Задача 2

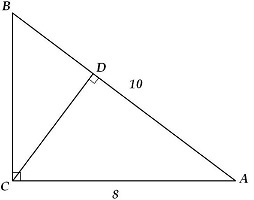
В прямоугольном треугольнике ABC сторона АС равна 8 см, сторона AB равна 10 см. Вычислить длину высоты CD.

Решение

1. Так как треугольники АВС и АСD подобны, можно составить пропорции сторон:

\(\frac{AB}{AC}=\frac{BC}{CD}\)

2. Найдем длину катета ВС:

\(BC=\sqrt{AB^2-AC^2}=\sqrt{10^2-8^2}=\sqrt{100-64}=36=6\)

\(ВС=6\) см

3. Далее подставим полученную величину в соотношение, записанное в первом пункте:

\(\frac{10}8=\frac6{CD}\)

Теперь выведем отсюда уравнение с неизвестным CD:

\(CD=\frac{8\times6}{10}=\frac{48}{10}=4,8\)

Ответ: CD=4,8 см.