Какие числа называют рациональными в математике

Рациональные числа в математике — какие так называются

К рациональным относят целые и дробные числа с положительным или отрицательным знаком, а также ноль. Например, 2, 0, -8, \(\frac47, 0,36.\)

Множество рациональных чисел не бесконечно, существуют примеры исключений. Доказательством тому служит множество иррациональных чисел. К примеру, рациональными не считают:

• некоторые корни — например, \(\sqrt2\);
• число Пи, число Эйлера, золотое сечение;
• непериодические дроби.

Для чего нужны, какой буквой обозначается

Для обозначения множества рациональных чисел используют букву Q. Это множество можно записать в виде:

\(Q=\left\{\frac mn\vert m\in Z,n\in N\right\}\)

Название множества произошло от латинского слова «ratio», которое означает «отношение», «дробь». То есть рациональные числа — это дробные числа. Их применяют при счете целых объектов и их частей — например, если порезать яблоко на несколько долек. 

Свойства рациональных чисел

Одно из основных свойств рациональных чисел — их замкнутость относительно всех арифметических операций.

Это свойство можно объяснить на примере натуральных чисел: 16+14=30. 30 — это натуральное число, как и его слагаемые. Это значит, что множество натуральных чисел замкнуто относительно операции сложения.

С помощью рациональных чисел можно выполнять любые арифметические операции:

• сложение: 3,5+2=5,5;
• умножение: \(-\frac45\cdot\frac54=-1\);
• вычитание: 1-7,6=-6,6;
• деление: \(3:8=\frac38\).

Таким образом, множество Q замкнуто относительно всех четырех операций.

Список свойств рациональных чисел широк. Его можно сократить до нескольких основных пунктов.

1. Упорядоченность. Между рациональными числами всегда можно идентифицировать один из видов отношений: «>», «<» или «=».
2. Транзитивность отношения порядка. Для любых трех рациональных чисел a, b, c верно следующее: если a<b, b<c, то a<c. Если a=b, b=c, то a=c.
3. Наличие противоположного числа. У любого рационального числа есть противоположное, при сложении с которым получается 0: a+(-a)=0.
4. Наличие обратного числа. Любое рациональное число имеет обратное ему число, при умножении на которое получается 1: \(\frac ab\cdot\frac ba=1\).
5. Аксиома Архимеда. Каким бы ни было рациональное число a, всегда можно взять столько единиц, что их сумма будет больше a: \(\sum_{k=1}^n1>a\)

Классификация рациональных чисел, виды с примерами

Выделяют несколько групп рациональных чисел.

1. Целые числа.
2. Обыкновенные дроби.
3. Десятичные дроби:

• конечные: после запятой стоит определенное количество цифр — например, 0,6; -4,657;
• бесконечные периодические: после запятой стоит бесконечное количество цифр, но одна или несколько из них повторяются. Такие повторяющиеся цифры называют периодом. Их записывают в скобках для краткости: \(0,33333\dots=0,\left(3\right).\)

Какая разница между целыми, натуральными и рациональными числами

Это понятие появилось раньше других. Натуральные числа используют для простого счета существующих в окружающем мире предметов. Ноль, отрицательные и дробные числа не входят в множество N. Оно замкнуто относительно операций сложения и умножения.

Исторически целые числа возникли как решение проблемы ограниченности натуральных чисел. С развитием математики стало известно о существовании нуля и отрицательных чисел. Однако множество Z не включает в себя дробные числа. Оно замкнуто относительно всех операций, кроме деления.

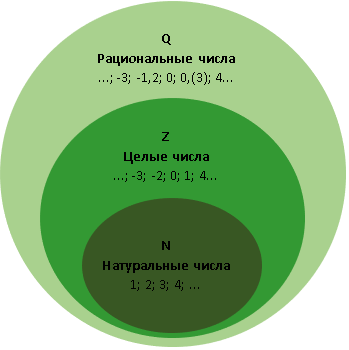
Множество рациональных чисел, исходя из определения, является наиболее широким из трех. Оно включает в себя все натуральные и целые числа.

Систему отношений между множествами можно представить в виде кругов Эйлера. Схема представлена ниже.