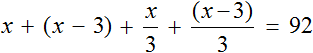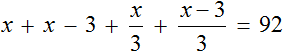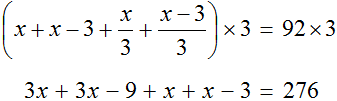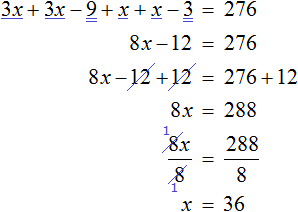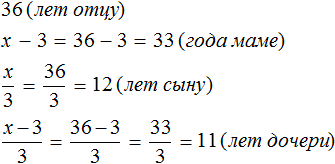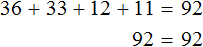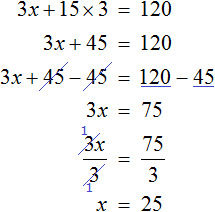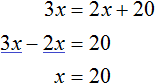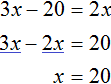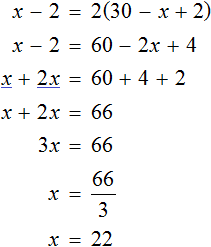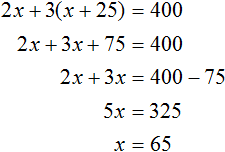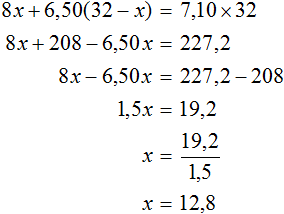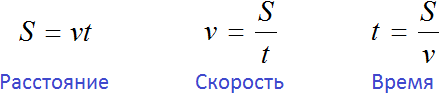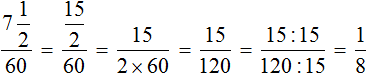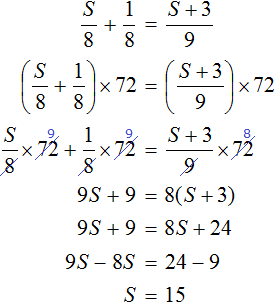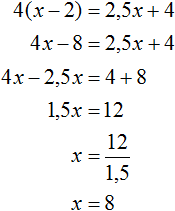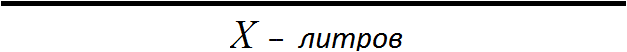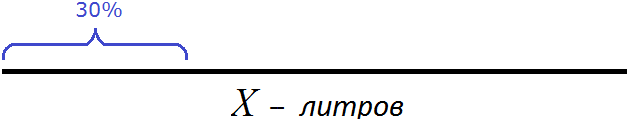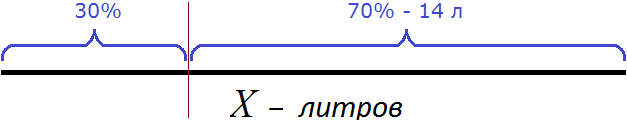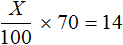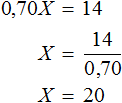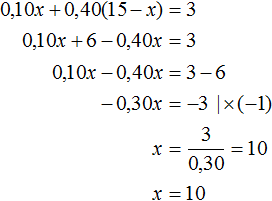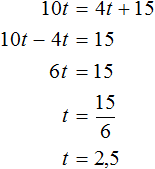Решение задач по математике с помощью уравнений
Для каких случаев подходит решение задач по математике с помощью уравнений
Под решением задач в алгебре подразумевается поиск какой-либо величины с помощью логических рассуждений и вычислений.
К примеру, необходимо определить скорость, время, путь, массу конкретного объекта, либо количество чего-либо. Подобные задания в математике решают с помощью уравнений. В процессе искомую величину принимают за переменную, которую можно рассчитать, используя логику и составляя уравнение. По результатам требуется проверить ответ, который должен соответствовать условиям задачи.
Уравнение является равенством, включающее в себя переменную, значение которой требуется определить.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Решить уравнение — значит, найти все его корни.
Корнем уравнения называется такое число, при подстановке которого в уравнение на место неизвестного получается справедливое числовое равенство.
Алгоритм решения текстовых задач с помощью уравнений, примеры
Уравнение позволяет существенно упростить решение задач. В первую очередь необходимо проанализировать условия, определить исходные величины и то, каким образом они связаны с неизвестными.
Стандартный алгоритм действий при решении задачи с помощью уравнения состоит из следующих этапов:
- обозначение неизвестной величины буквой;
- составление уравнения в виде формулы на основе условий задачи;
- решение уравнения с объяснением;
- запись ответа.
Распространенные приемы, используемые в процессе решения уравнений:
- перенос числа из одной части уравнения в другую со сменой знака на противоположный;
- деление или умножение обеих частей уравнения на какое-либо одинаковое число, не равное нулю, чтобы снизить степень его сложности.
Наиболее простым методом решения является составление буквенных выражений, которые описывают ситуацию, согласно условиям задачи. Можно рассмотреть данный способ на примере.
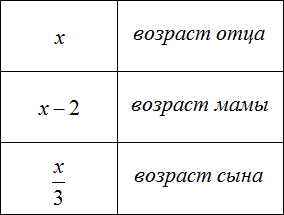
По условиям задачи отцу х лет. Мама младше его на два года. Возраст сына меньше в три раза по сравнению с возрастом отца. Требуется записать возраст каждого члена семью, используя выражения.
Решение:
Предположим, что отцу х лет. Мама на три года младше, чем отец. Возраст сына в три раза меньше, чем возраст отца. Возраст дочери в три раза меньше, чем возраст матери. Необходимо определить возраст членов семьи, если вместе им 92 года.
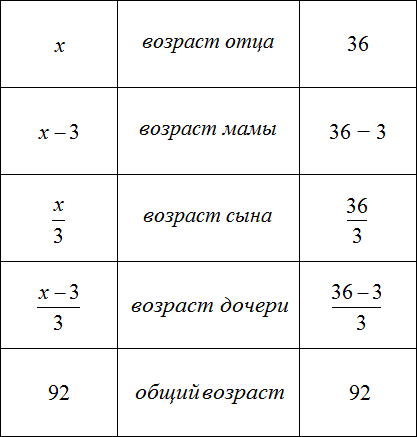
В первую очередь можно обозначить возраст отца переменной х, а затем записать остальные выражения:
Далее следует записать общее выражение:
После раскрытия скобок получим:
Исключить дроби можно, если умножить обе части уравнения на 3:
Уравнение можно решить с помощью тождественных преобразований:
Зная, сколько лет отцу, можно рассчитать возраст остальных членов семьи:
Результат можно проверить:
Предположим, что цена килограмма яблок равна х рублей. Необходимо записать выражение для определения количества яблок, которое можно приобрести на 300 рублей. Тогда ответ будет записан так: \(\frac{300}{x}\) килограмм яблок. Данное выражение справедливо, так как при цене яблок 50 рублей, на 300 рублей можно купить \(\frac{300}{50}\) или 6 килограмм яблок.
Нередко встречаются более сложные задачи.
Том, Джон и Лео купили в столовой по бутерброду и чашке кофе. Цена бутерброда х рублей, а кофе — 15 рублей. Требуется рассчитать, сколько стоит бутерброд, если общая сумма покупки составила 120 рублей. Ответ можно найти достаточно просто, если из 120 рублей отнять стоимость трех чашек кофе (15 * 3), и поделить полученный результат на 3:
Однако целью задачи является поиск решения с помощью уравнения. Сначала нужно выразить стоимость всех бутербродов: 3х. Стоимость трех чашек кофе будет равна: 15 * 3. Уравнение примет вид:
Таким образом, бутерброд стоит 25 рублей.
Методика обучения решению текстовых задач с помощью уравнения
Решение задачи будет справедливым в том случае, когда уравнение составлено корректно. По сравнению со стандартными уравнениями, для которых выполняют поиск корней, уравнения, предназначенные для решения задач, обладают собственным конкретным применением. Любой из компонентов такого выражения можно описать с помощью словесной формы.
При составлении уравнения требуется понимание цели, с которой данный компонент включен в выражение. Кроме того, уравнение является равенством. В результате решения левая и правая часть выражения должны быть равны. Эта идея является ключевой при составлении уравнения. Можно предположить, что уравнение является весами, состоящими из пары чаш и экрана, демонстрирующего состояние весов.
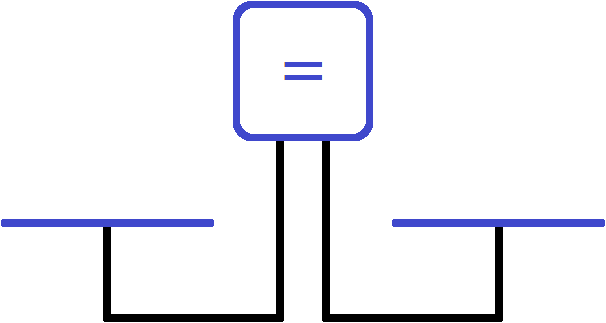
На рисунке можно наблюдать равновесное состояние весов. Так как чаши пусты, они равны между собой. Такое положение можно записать, как:
0=0
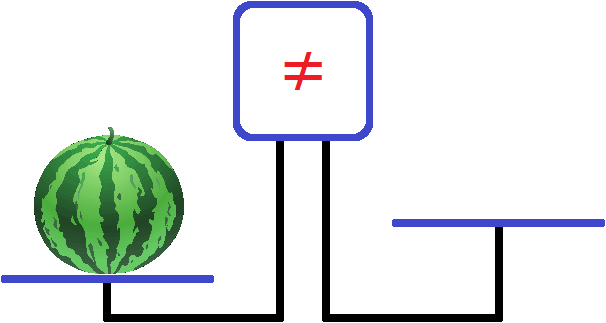
Затем на одну из чаш поместили арбуз:
В результате левая чаша весов будет перевешивать правую. На экране отображается знак неравенства (\neq). Можно сделать вывод о том, что левая чаша весов не равна правой чаше. Далее следует приступить к решению задачи. Например, необходимо определить вес арбуза, который поместили на левую чашу. Решение заключается в составлении уравнения, роль которого играют непосредственно весы. Массу арбуза можно принять за переменную. В процессе требуется корректно составить выражение, то есть выровнять весы, таким образом, чтобы можно было рассчитать вес арбуза. Для этого на правую чашу следует поместить какой-то тяжелый предмет. К примеру, пусть это будет гиря массой 7 килограмм.
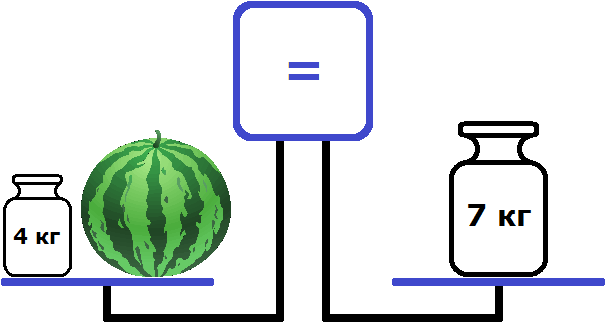
В результате ситуация изменилась. Правая чаша стала тяжелее, чем левая. На экране все еще отображается знак неравенства. Следует добавить гирю на левую чашу массой 4 килограмма.
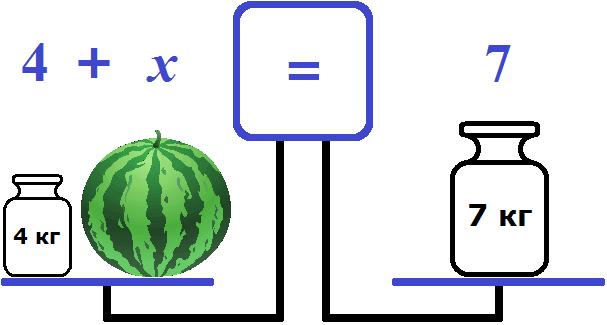
После проделанных манипуляций весы пришли в состояние равновесия. Уровни, на которых расположены чаши, сравнялись. На экране показан знак равенства. Таким образом, левая чаша равна правой чаше. С помощью последовательных действий удалось получить уравнение в виде равенства с одним неизвестным. Левая чаша представляет собой левую часть уравнения, состоящую из элементов: число 4 и переменная х. Правая чаша включает только компонент в виде числа 7.
Уравнение: \(4 + х = 7\)
Корень уравнения: 3
Можно сформулировать ответ задачи: масса арбуза составляет 3 килограмма.
С помощью аналогичной методики можно решать и другие задачи. Для вычисления какого-нибудь неизвестного к левой и правой частям уравнения добавляют определенные компоненты такие, как:
- слагаемые;
- множители;
- выражения.
Как правило, подобные элементы даны в условиях задачи. Требуется лишь корректно структурировать их и составить уравнение. В предыдущем примере был использован метод подбора необходимой гири для расчета веса арбуза.
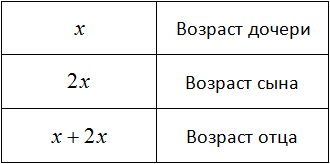
В качестве другого примера можно рассмотреть задачу, по условию которой возраст отца равен общему количеству лет сына и дочери. При этом сын старше дочери в два раза и на двадцать лет моложе, чем отец. Требуется рассчитать возраст каждого члена семьи. Обозначив возраст дочери за х, можно записать возраст сына, который составит 2х. Сумма их возрастов будет записана, как х + 2х.
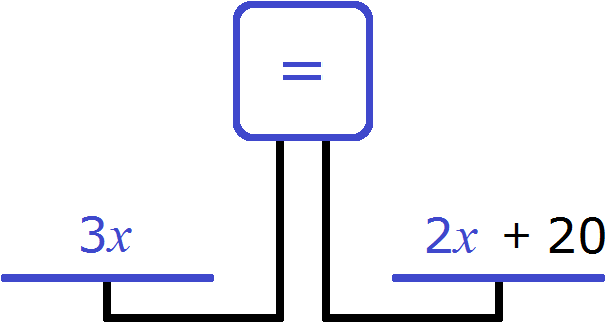
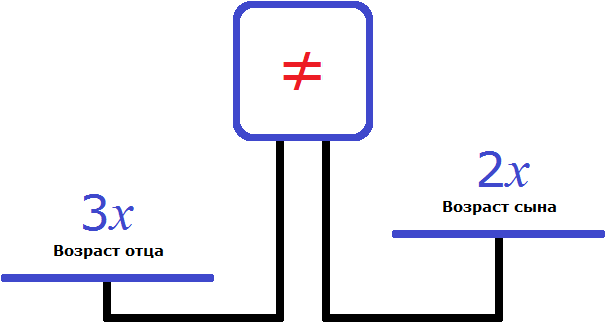
Далее можно привести подобные слагаемые в выражении х + 2х. Таким образом, возраст отца составит 3х. Затем необходимо решить уравнение. Для этого необходимо записать равенство, в котором можно определить неизвестное х. Наглядно продемонстрировать решение помогут весы. Предположим, что на левой чаше находится возраст отца (3х), а на правой чаше — возраст сына (2х).
На экране отображается знак неравенства. Левая чаша перевешивает правую по той причине, что отец старше сына. Для того чтобы уравнять весы, требуется рассчитать неизвестное х. Следует прибавить какое-либо число к правой чаше. Согласно условиям задачи, этим числом является 20 лет, так как сын моложе отца на 20 лет. В результате добавления к правой чаше весов 20 лет весы примут состояние равновесия.
Можно записать уравнение, которое достаточно просто решить:
В самом начале за переменную х был принят возраст дочери. Получается, что дочери 20 лет. Возраст сына будет равен (20 * 2), то есть 40 лет. Для того чтобы определить, сколько лет отцу, требуется сложить возраст сына и дочери, то есть (20 + 40).
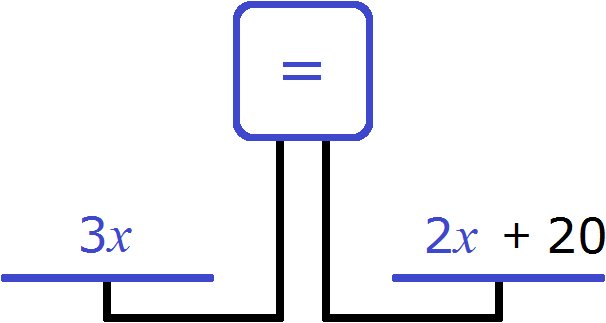
Следует обратить внимание на один из этапов решения задачи, когда при постановке возраста сына и отца на весы левая чаша оказалась тяжелее правой.
Проблема неравенства чаш была решена путем добавления к правой чаше 20 лет. Таким образом, можно записать равенство: \(3х = 2х + 20\)
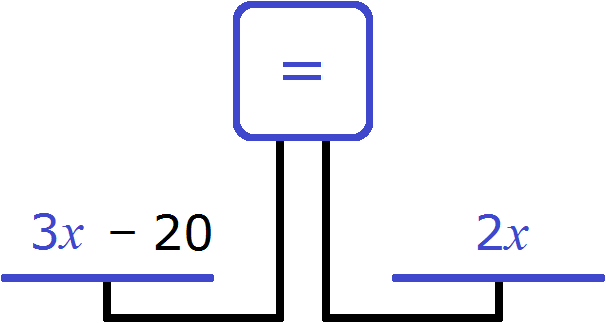
Другой способ заключается в вычитании этих 20 лет из левой чаши весов. В данном случае также было бы получено записанное равенство.
Второе уравнение будет иметь вид: \(3х – 20 = 2х\). Корень уравнения в любом случае равен 20.
Исходя из такого анализа, можно заключить, что уравнения \(3х = 2х + 20\) и \(3х – 20 = 2х\) равносильны. Согласно определению, равносильные уравнения обладают одинаковыми корнями. При детальном рассмотрении можно заметить, что второе уравнение получено в результате переноса числа 20 из правой части в левую с заменой знака на противоположный, что не влияет на корни уравнения.
Следует отметить, что в самом начале решения задачи возрасты отца, сына и дочери допустимо выразить через другие выражения. Например, пусть сыну х лет, тогда дочери \(\frac{x}{2}\) лет. Возраст отца в таком случае составит \(x+ \frac{x}{2}\). Для того чтобы записать логически правильное уравнение, необходимо требуется прибавить число 20 к возрасту сына, так он на 20 лет старше отца. Теперь можно приступить к решению уравнения.
Ответ задачи не поменялся. Возраст сына составляет 40 лет. Дочери 20 лет, а отцу — 60 лет. Задачу можно решить разными методами. Поэтому для любого, даже самого сложного примера, достаточно легко подобрать оптимальный способ решения.
Примеры решения задач
Две пачки содержат 30 тетрадей. Если переложить из первой пачки во второй пару тетрадей, то в первой пачке станет в два раза больше тетрадей, чем во второй. Необходимо определить начальное количество тетрадей в каждой пачке.
Решение:
Количество тетрадей, которые находились изначально в первой пачке, можно принять за х. Согласно условиям задачи, во второй пачке будет 30 – х тетрадей.
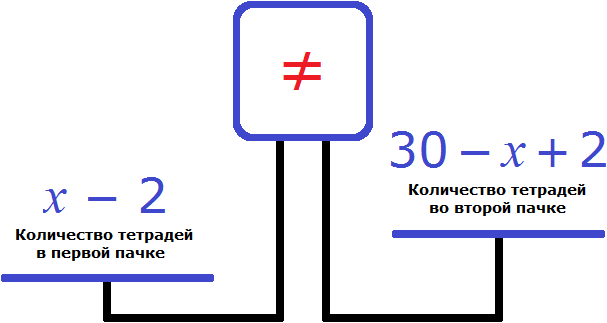
При перемещении двух тетрадей из первой пачки во вторую, в первой пачке будет содержаться в два раза больше тетрадей, чем во второй. Таким образом:
30 - х +2
Далее выражения принимают такой вид:
Из записанных выражений следует составить уравнение. Можно воспользоваться весами, на чаши которых поместили две пачки тетрадей.
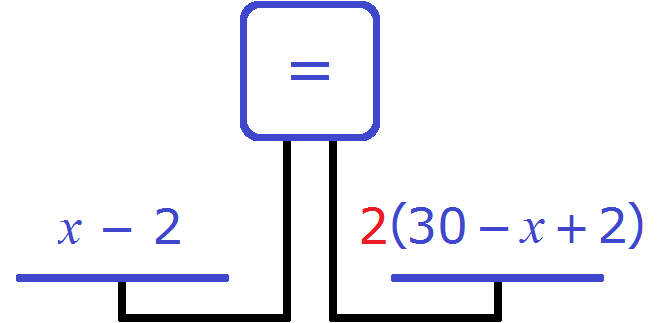
Левая чаша перевешивает правую, что следует из условия задачи. Для того чтобы весы приняли равновесное положение, необходимо увеличить правую часть в два раза путем умножения на 2.
Полученное уравнение можно решить:
Так как правая пачка была принята за неизвестное, то ее значение равно 22 тетрадям. Вторая пачка равна 30 – х, то есть 8 тетрадям.
Ответ: в первой пачке было 22 тетради, а во второй — 8 тетрадей.
Два человека занимались чисткой картофеля. Первый выполнял работу со скоростью 2 картофелины в минуту, в второй — три картофелины в минуту. Общий объем очищенного картофеля составил 400 штук. Требуется определить время работы каждого человека, если второй проработал на 25 минут дольше, чем первый.
Решение:
Время, в течение которого работал первый человек, можно принять за х. Исходя из условий задачи, время работы второго составит х + 25. Количество картофеля, который очистил первый человек составит 2х, так как он чистил 2 штуки в минуту. Аналогично можно вычислить количество картофеля, который очистил второй человек. Число картофелин составит 3(х + 25). Общее количество очищенного картофеля равно 400 штук.
При наличии исходных данных можно составить уравнение, в левой части которого учтен картофель, очищенный каждым человеком, а в правой — общее количество:
Начиная решать задачу, в качестве переменной х было выбрано время работы первого человека. Таким образом, он чистил картофель в течение 65 минут. Тогда второй человек затратил на выполнение работы х + 25 или 90 минут.
Ответ: время работы первого человека составило 65 минут, а второго — 90 минут.
Смесь чая весит 32 килограмма. Цена первого сорта чая равна 8 рублей, второго — 6,5 рублей. Стоимость килограмма смеси составляет 7,1 рублей. Требуется определить вес каждого сорта чая в смеси.
Решение:
За х можно принять массу чая первого сорта. В таком случае второй сорт чая будет весить 32 – х.
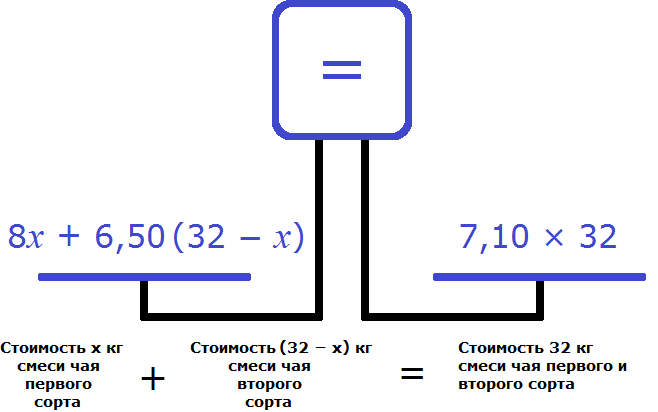
Цена килограмма чая первого сорта составляет 8 рублей. Тогда х килограмм чая будет стоить 8х рублей. Килограмм чая второго сорта стоит 6,5 рублей. Стоимость 32 – х килограмм чая равна 6,5(32 – х). Для того чтобы узнать, сколько стоит 32 килограмма смеси, требуется 7,10 рублей умножить на 32 килограмма.
Далее можно воспользоваться весами. Предположим, что на левой чаше стоимость смесей чая первого и второго сорта, а на правой — стоимость 32 килограмм смеси, то есть общая стоимость смеси из двух сортов чая.
В итоге можно решить полученное уравнение:
В качестве переменной х выступает масса чая первого сорта. Таким образом, она составит 12,8 килограмм. Из выражения 32 – х можно рассчитать массу чая второго сорта. Она будет равна 19,2 килограмм.
Ответ: смесь состоит из 12,8 кг чая первого сорта и 19,2 кг чая второго сорта.
Велосипедист преодолел некоторое расстояние со скоростью 8 км/ч. Обратный путь пролегал по другой дороге, которая длиннее на 3 км, чем первая. Возвращаясь, велосипедист ехал со скоростью 9 км/ч и затратил на путь на 7,5 мин больше. Требуется определить длину первой и второй дороги.
Решение:
Следует рассмотреть зависимость расстояния, времени и скорости:
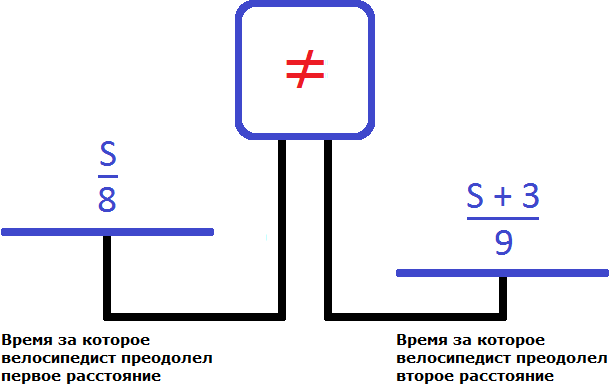
Примем длину первой дороги за S. Велосипедист преодолел этот путь со скоростью 8 км/ч. Время пути равно S/8. Обратная дорога длиннее на 3 км. Поэтому ее длину можно обозначить, как S + 3. Этот путь велосипедист проехал со скоростью 9 км/ч. Таким образом, время обратного пути составляет (S + 3)/9. Получив исходные данные, можно составить уравнение:
На весах правая чаша будет перевешивать левую, так как на обратный путь велосипедист потратил на 7,5 минут больше. Следует перевести минуты в часы и прибавить этот компонент к обеим чашам.
Далее можно решить уравнение:
Переменная S выражает расстояние первой дороги. Таким образом, первый путь составит 15 км. Вторая дорога равна S + 3, то есть 18 км.
Ответ: длина первой дороги 15 км, второй — 18 км.
По шоссе движутся два автомобиля с равными скоростями. При увеличении скорости первой машины на 10 км/ч, вторая машина снижает скорость на 10 км/ч. В таком случае за 2 ч первый автомобиль пройдет столько же, сколько второй за 3 ч. Необходимо определить начальные скорости автомобилей.
Решение:
Предположим, что v — это скорость каждого автомобиля. Согласно условиям задачи:
v + 10
v - 10
Со скоростью v + 10 первый автомобиль преодолеет 2(v + 10) км, а второй — 3(v – 10) км. В данном случае машины пройдут одинаковые расстояния, поэтому можно составить справедливое равенство и решить его.
Так как по условию задачи скорость автомобилей одинакова и принята за v, можно заключить, что данная скорость составляет 50 к/ч.
Ответ: скорость автомобилей 50 км/ч.
В ремонтных работах участвовало в 2,5 раза больше маляров, чем плотников. Позже к бригаде присоединились еще 4 маляра, а два плотника ушли. В итоге маляров в бригаде оказалось в 4 раза больше, чем плотников. Необходимо рассчитать изначальное количество маляров и плотников.
Решение:
За х можно принять первоначальное количество плотников. Оно является целым числом, больше нуля и включено в множество натуральных чисел. Число маляров в 2,5 раза больше, чем плотников, то есть 2,5х.
Далее бригада пополнилась 4 малярами, а два плотника ее покинули. Можно уменьшить число плотников на 2, то есть х – 2. Количество маляров можно увеличить на 4, то есть 2,5х + 4.
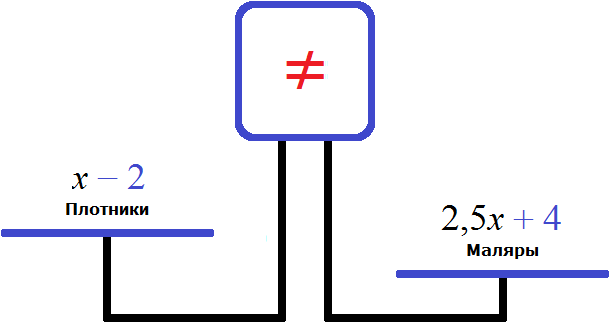
Полученные выражения следует записать в виде уравнения:
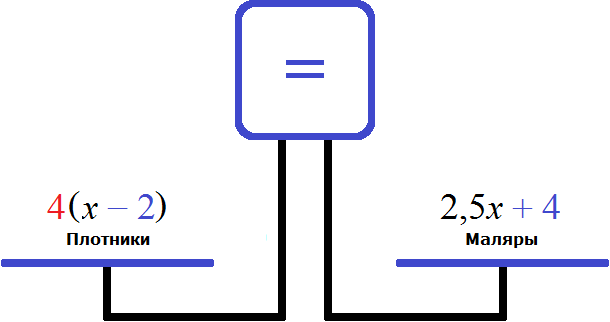
Правая чаша перевешивает левую, так как после включения в бригаду еще четырех маляров, и перемещения двух плотников на другой объект, количество маляров в бригаде оказалось в 4 раза больше чем плотников. Чаши придут в состояние равновесия, если левую чашу увеличить в 4 раза.
Получилось уравнение, которое необходимо решить:
Переменная х обозначает начальное число плотников. Исходя из решения, оно составило 8 человек. Количество маляров 2,5х равно 20 человек. Полученные значения являются неотрицательными и целыми, относятся к множеству натуральных чисел.
Ответ: вначале на объекте работали 8 плотников и 20 маляров.
Из бидона взяли 30% молока. Остаток составил 14 л. Необходимо найти, сколько литров молока находилось в бидоне.
Решение:
Предположим, что в начале в бидоне было х литров. Можно представить его в виде линии.
Далее можно графически представить ситуацию, когда из бидона отлили 30% молока.
Процентом называют одну сотую часть чего-либо. При заборе 30% молока в бидоне осталось 70% молока. Эти 70% представляют собой 14 литров молока, согласно условию задачи.
Далее можно составить уравнение. Важно учитывать, что для расчета процента от числа требуется общее количество разделить на 100 и умножить на количество процентов. Применим утверждение к задаче:
Ответ: первоначально в бидоне было 20 литров молока.
Имеется два сплава из золота и серебра. В одном металлы содержатся в соотношении 1:9, а во втором — 2:3. Требуется определить вес каждого сплава, необходимого для изготовления 15 кг нового сплава, в котором золото и серебро относились бы как 1:4.
Решение:
В первую очередь необходимо определить содержание золота и серебра в 15 кг нового сплава. Согласно соотношению 1:4, одна часть сплава должна состоять из золота, а четыре — из серебра. Общее количество частей равно 1 + 4 или 5. В таком случае, одна часть будет весить 15/5 или 3 кг.
Далее нужно рассчитать вес золота в 15 кг сплава. Для этого 3 кг умножим на 1 часть. Получим 3 кг золота. Аналогично можно определить, что количество серебра в сплаве составит 3 * 4 = 12 кг.
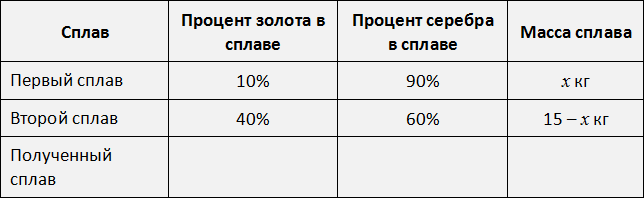
Таким образом, в сплаве весом 15 кг содержится 3 кг золота и 12 кг серебра. Предположим, что масса первого сплава равна х, а второго — 15 – х, исходя из условий задачи.
Затем необходимо выразить все отношения в процентах. Первый сплав состоит из золота и серебра в соотношении 1:9. Общее количество частей составит 1 + 9 = 10. Золото будет составлять 1/10 * 100 = 10%, а серебро — 9/10 * 100 = 90%.
Таким же образом можно определить концентрацию металлов во втором сплаве. Их соотношение составит 2:3. Общее количество частей равно 2 + 3 = 5. На золото приходится 2/5 * 100 = 40%, а на серебро — 3/5 * 100 = 60%.
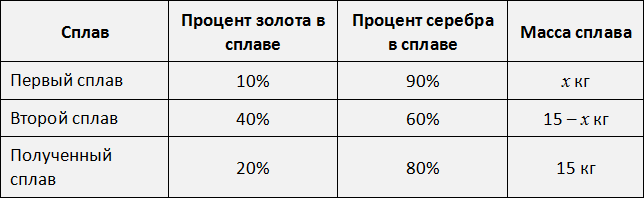
Новый сплав весом в 15 кг содержит 3 кг золота, а именно 3/15 * 100 = 20%, а также 12/15 * 100 = 80% серебра.
Согласно полученным табличным данным, можно записать уравнение. Для упрощения задачи следует выразить проценты в десятичных дробях. Таким образом, первый сплав содержит 0,10х золота, а второй — 0,40(15 – х) золота. В результате в полученном сплаве масса золота будет суммой масс золота первого и второго сплавов и эта масса составляет 20% от нового сплава. А 20% от нового сплава это 3 кг золота, вычисленные нами ранее. Можно составить справедливое равенство и решить его:
За х приняли вес первого сплава. Из расчетов следует, что его масса равна 10 кг. В таком случае, масса второго сплава составит 15 – 10 или 5 кг.
Ответ: получить новый сплав весом 15 кг можно из 10 кг первого и 5 кг второго сплавов.
Всадник догоняет пешехода, который находится впереди него на 15 км. Необходимо определить время, за которое всадник догонит пешехода при условии, что каждый час он проезжает по 10 км, а пешеход преодолевает по 4 км.
Решение:
Рассматриваемый пример представляет собой задачу на движение. Решение заключается в определении скорости сближения, на которое затем нужно поделить начальное расстояние между всадником и пешеходом. Скорость сближения можно рассчитать, вычитая из большей скорости меньшую, то есть 10 – 4 = 6 км/ч
Каждый час расстояние в 15 км сокращается на 6 км. Для того чтобы определить, когда всадник догонит пешехода, следует 15/6. Получим 2,5 часа. Данное значение представляет собой 2 целых часа и 30 минут. Таким образом, всадник догонит пешехода через 2 часа 30 минут.
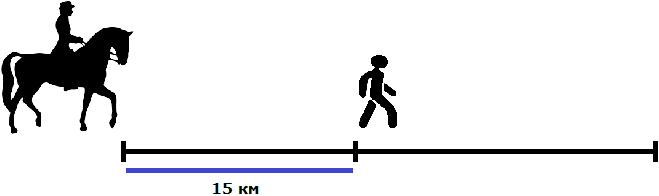
Полученную задачу можно решить, используя уравнение. Предположим, что начальные точки пути для всадника и пешехода совпадают. При этом пешеход вышел раньше и успел пройти 15 км.
Путь всадника начинается после старта пешехода. Его скорость составляет 10 км/ч. Пешеход движется со скоростью 4 км/ч. Таким образом, всадник в течение определенного времени догонит пешехода. Время — это искомая величина, которую нужно рассчитать. Расстояние, которое прошли всадник и пешеход, равно S = vt
Всадник преодолел расстояние 10t, а пешеход — 4t + 15. В момент, когда путники поравняются, их пройденное расстояние будет одинаковым. Таким образом:
10t = 4t + 15
Полученное уравнение достаточно просто решить:
Ответ: всадник догонит пешехода через 2,5 часа.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так