Радиус окружности, описанной около правильного шестиугольника
Что такое окружность, описанная около правильного шестиугольника
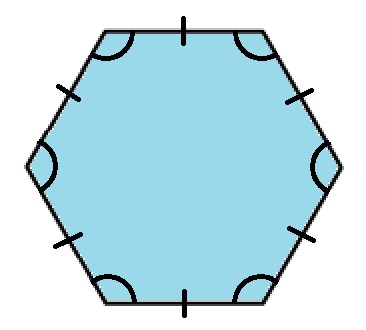
Правильный шестиугольник — выпуклый шестиугольник, у которого все стороны и углы равны.
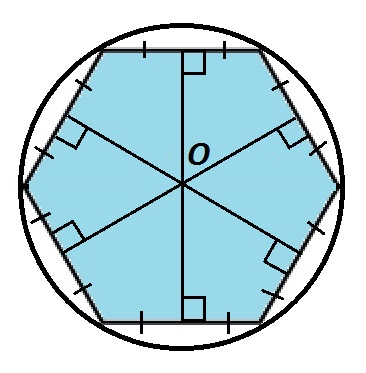
Описанная около многоугольника окружность — это окружность, которая содержит все вершины выпуклого многоугольника. Ее центром является точка пересечения срединных перпендикуляров к сторонам многоугольника, обычно её обозначают прописной буквой О.
Как найти радиус, формула
Для расчетов используем формулу радиуса окружности, описанной около правильного многоугольника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(R=\frac a{2\sin\left(\frac{360^0}{2n}\right)}\)
где R — радиус описанной окружности правильного многоугольника,
а — длина стороны многоугольника,
n — количество сторон (или вершин) многоугольника.
Подставим в формулу значение n=6.
\(R=\frac a{2\sin\left(\frac{360^0}{2n}\right)}=R=\frac a{2\sin\left(\frac{360^0}{2·6}\right)}=\frac a{2\sin\left(\frac{360^0}{12}\right)}=\frac a{2\sin30^0}.\)
Так как \(sin30^0=\frac12\), то \(R=\frac a{2\sin30^0}=\frac a{2·\frac12}=\frac a1\). Получаем формулу радиуса окружности, описанной около правильного шестиугольника:
R=a
где R — радиус описанной окружности,
а — сторона правильного шестиугольника.
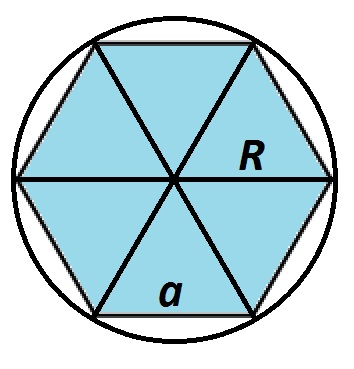
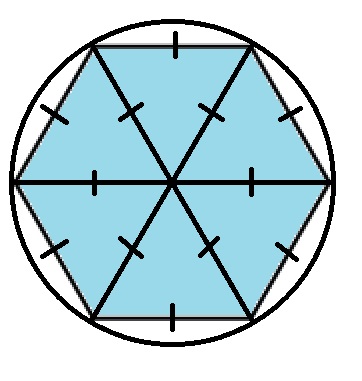
Эту же формулу модно найти и другим способом. Биссектрисы углов правильного шестиугольника разбивают его на шесть равных равносторонних треугольников. Точка пересечения биссектрис у правильного шестиугольника совпадает с точкой пересечения срединных перпендикуляров и является центром описанной окружности. Расстояние между центром окружности и вершиной шестиугольника равно радиусу описанной окружности и стороне равностороннего треугольника. Этот отрезок также равен стороне шестиугольника.
Свойства окружности, описанной около шестиугольника
- У правильного шестиугольника центры вписанной и описанной окружностей совпадают.
- Диаметр описанной окружности совпадает с большей диагональю правильного шестиугольника и равен его удвоенной стороне.
Площадь круга, ограниченного описанной окружностью
Чтобы вычислить площадь круга, ограниченного описанной окружностью правильного шестиугольника, используем стандартную формулу площади круга.
\(S=π·r^2\)
где S — площадь круга,
π — коэффициент, число π,
r — радиус круга.
Так как радиус круга равен стороне правильного шестиугольника, около которого описана окружность, получаем формулу:
\(S=π·а^2\)
где S — площадь круга,
π — коэффициент, число π,
а — сторона правильного шестиугольника.
Пример расчета радиуса окружности, описанной около шестиугольника
Дано: около правильного шестиугольника описана окружность. Меньшая диагональ правильного шестиугольника равна \(5\sqrt3 см.\)
Найти: радиус описанной окружности.
Решение: Обозначим сторону правильного шестиугольника как а. Тогда его меньшая диагональ будет \(а\sqrt3 см\). Следовательно, а=5 см. Радиус окружности, описанной около правильного шестиугольника равен его стороне. R=5 см.
Ответ: 5 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так