Окружность, вписанная в правильный шестиугольник

Содержание:

Содержание

Что такое правильный шестиугольник

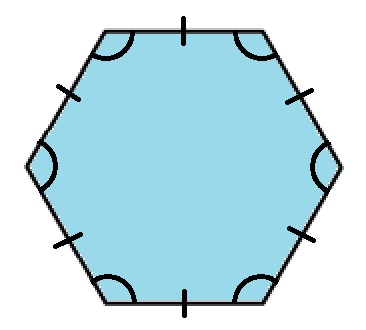
Правильный шестиугольник или гексагон — выпуклый шестиугольник, у которого все стороны и углы равны.

Сумма всех углов n–угольника равна 180°(n−2). Каждый угол правильного n–угольника равен \(α_n=\frac{\left(n-2\right)}n180°\). Следовательно углы правильного шестиугольника равны \(\frac{\left(6-2\right)}6180°=120°\).

Основные свойства правильного шестиугольника

У гексагона все внутренние углы равны между собой.
Каждый внутренний угол правильного шестиугольника равен 120°.
Все стороны гексагона равны между собой.
Радиус окружности, описанной около правильного шестиугольника, равен его стороне.
Большая диагональ правильного шестиугольника равна диаметру описанной около него окружности или сумме двух его сторон.
Меньшая диагональ правильного шестиугольника в \(\sqrt3\)раз больше его стороны.
Меньшая диагональ правильного шестиугольника и две его противолежащие стороны перпендикулярны друг другу.
Меньшая диагональ правильного шестиугольника равна удвоенному радиусу вписанной в него окружности.
Правильный шестиугольник замещает плоскость, это значит заполняет ее без пробелов и наложений.
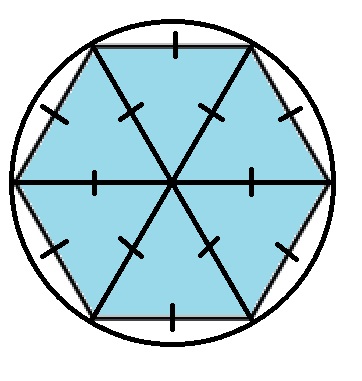
Диагонали правильного шестиугольника пересекаются в одной точке и делят его на 6 равных равносторонних треугольников. Высота этих треугольников равна радиусу вписанной в правильный шестиугольник окружности.
При поворотах относительно центра на угол, кратный 60°, правильный шестиугольник переходит в себя.
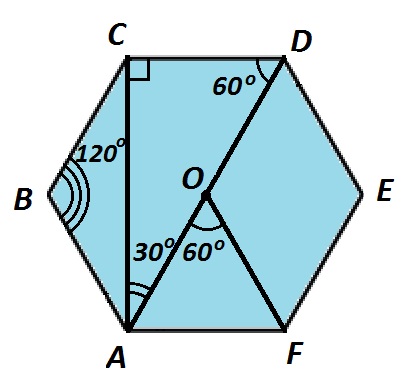
Треугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями — прямоугольный. Гипотенузой такого треугольника является большая диагональ. Его острые углы равны 30° и 60°.

У изображенного правильного шестиугольника ∠А=∠В=∠С=∠D=∠Е=∠F=120°. Стороны равны между собой АВ=ВС=СD=DE=EF=FA. Точка О — центр пересечения диагоналей. Большая диагональ AD=2АВ. Меньшая диагональ \(СА=\sqrt3·АВ\).

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Теорема 1

В любой правильный шестиугольник можно вписать окружность, и притом только одну.

Следствие из теоремы:

Центры вписанной и описанной окружности у правильного шестиугольника (как и у любого правильного многоугольника) совпадают.
Радиус вписанной окружности равен перпендикуляру, проведенному из центра к любой стороне правильного шестиугольника.

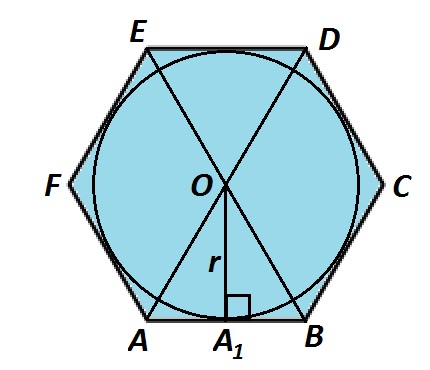
Нахождение радиуса вписанной окружности

шестиугольник правильный вписанная окружность.jpg

В шестиугольник АВСDEF вписана окружность. Ее центр находится на пересечении диагоналей в точке О. Если известна сторона данного шестиугольника, то можно найти радиус вписанной окружности, рассмотрев прямоугольный треугольник \(А_1ОВ\). Гипотенуза \(ΔА_1ОВ\) равна стороне шестиугольника, ОВ=АВ. Перпендикуляр \(ОА_1\) делит сторону АВ пополам, то есть \(А_1В=\frac12·АВ=\frac12·ОВ\). Так как \(ОВ^2=ОА_1^2+А_1В^2\), то \(ОА_1=\sqrt{ОB^2-A_1В^2}=\sqrt{ОB^2-A_1В^2}=\sqrt{0B^2-\left(\frac12\cdot0B\right)^2}=\frac{\sqrt3}2OB\). Получаем следующую формулу:

Формула 1

\(r=\frac{\sqrt3}2·a\)

где r — радиус окружности, вписанной в правильный шестиугольник,

а — сторона правильного шестиугольника.

Классическая формула для нахождения радиуса вписанной окружности правильного многоугольника

Существует классическая формула, с помощью которой можно вычислить радиус окружности, вписанной в любой правильный многоугольник.

Формула 2

\(r=\frac a{2tg\frac{180^0}n}\)

где r — радиус окружности, вписанной в правильный многоугольник,

а — сторона правильного многоугольника,

n — количество вершин многоугольника.

Для правильного шестиугольника n=6.

\(r=\frac a{2tg\frac{180^0}6}=\frac a{2tg30^0}.\)

Так как \(tg30^0=\frac1{\sqrt3}\), то \(r=\frac{\sqrt3}2·a\). То есть, получаем формулу, найденную выше.

Периметр правильного шестиугольника

Если известен радиус вписанной окружности, то периметр правильного шестиугольника можно найти по формуле:

Формула 3

\(Р=4\sqrt3r\)

где Р — периметр правильного шестиугольника,

r — радиус вписанной в него окружности.

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 2)

Заметили ошибку?

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»